5-5 Light has properties of both waves and particles
At the end of the nineteenth century, physicists mounted a valiant effort to explain how a material can produce blackbody radiation. To this end they constructed theories based on Maxwell’s description of light as electromagnetic waves. But while electromagnetic waves could explain many properties of light, it was not until the discovery of photons that all features of blackbody curves could be understood.
The Discovery of Photons
In 1905, the great physicist Albert Einstein developed a radically new model for the nature of light. Central to this new picture is that light is made out of particles! Each particle of light is called a photon, which is a distinct packet of electromagnetic energy.
Light is made of smaller entities called photons, each one with a wavelength of its own
Photons have a dual nature in that they are both particlelike and wavelike. They are particlelike in the sense that they are the small packets of energy that make up light. As expected with particles, you can count the number of photons in an electromagnetic wave. But, photons are also wavelike because each one is itself a wave, where each photon has the same wavelength as the electromagnetic wave of which it is a small part. As expected with waves, photons exhibit interference patterns when passed through a double-slit experiment like the one in Figure 5-5.
The energy of each photon is related to the wavelength of light: the longer the wavelength, the lower the energy. Thus, a photon of red light (wavelength λ = 700 nm) has less energy than a photon of violet light (λ = 400 nm). Conversely, the shorter a photon’s wavelength, the higher its energy.
120
It was quickly realized that photons explain more than just blackbody curves, and now the study of photons plays a key role in almost every branch of science. While scientific equipment is usually needed to detect individual photons, there is a somewhat familiar effect that photons can help to explain. When it comes to tanning, your skin must be exposed to ultraviolet light. For example, a low intensity exposure to ultraviolet light causes tanning, but even a high intensity exposure of visible light will not cause the skin to darken. (Recall that you do not get tanned with regular indoor lighting, which has negligible UV light). The reason is that tanning, at the molecular level, results from a chemical reaction in the skin that involves a single photon. A single high-energy, short-wavelength ultraviolet photon can trigger a tanning reaction. However, even many lower-energy, longer-wavelength photons of visible light cannot trigger the reaction. In this situation, we see that it is not the total energy of light that matters, but how the energy is bundled into packets—and that is a photon.
The Energy of a Photon
The relationship between the energy E of a single photon and the wavelength of the electromagnetic radiation can be expressed in a simple equation:
Energy of a photon (in terms of wavelength)
The value of the constant h in this equation, now called Planck’s constant, has been shown in laboratory experiments to be
h = 6.625 × 10−34 J s
The units of h are joules multiplied by seconds, called “joule-seconds” and abbreviated J s.
Because the value of h is so tiny, a single photon carries a very small amount of energy. For example, a photon of red light with wavelength 633 nm has an energy of only 3.14 × 10−19 J (Box 5-3), which is why we ordinarily do not notice that light comes in the form of photons. Even a dim light source emits so many photons per second that it seems to be radiating a continuous stream of energy.
The energies of photons are sometimes expressed in terms of a small unit of energy called the electron volt (eV). One electron volt is equal to 1.602 × 10−19 J, so a 633-nm photon has an energy of 1.96 eV. If energy is expressed in electron volts, Planck’s constant is best expressed in electron volts multiplied by seconds, abbreviated eV s:
h = 4.135 × 10−15 eV s
Because the frequency ν of light is related to the wavelength λ by ν = c/λ, we can rewrite the equation for the energy of a photon as
Energy of a photon (in terms of frequency)
The equations E = hc/λ and E = hν are together called Planck’s law. Both equations express a relationship between a particlelike property of light (the energy E of a photon) and a wavelike property (the wavelength λ or frequency ν).
ASTRONOMY DOWN TO EARTH
Photons at the Supermarket
A beam of light can be regarded as a stream of tiny packets of energy called photons. The Planck relationships E = hc/λ and E = hν can be used to relate the energy E carried by a photon to its wavelength λ and frequency ν.
As an example, the laser bar-code scanners used at stores and supermarkets emit orange-red light of wavelength 633 nm. To calculate the energy of a single photon of this light, we must first express the wavelength in meters. A nanometer (nm) is equal to 10−9 m, so the wavelength is
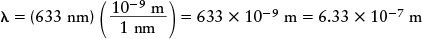
Then, using the Planck formula E = hc/λ, we find that the energy of a single photon is
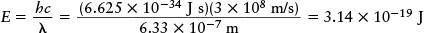
This amount of energy is very small. The laser in a typical bar-code scanner emits 10−3 joule of light energy per second, so the number of photons emitted per second is
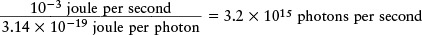
This number is so large that the laser beam seems like a continuous flow of energy rather than a stream of little energy packets.
121
The photon picture of light is essential for understanding the detailed shapes of blackbody curves. As we will see, it also helps to explain how and why the spectra of the Sun and stars differ from those of perfect blackbodies.
CONCEPT CHECK 5-9
If a photon’s wavelength is measured to be longer than the wavelength of a green photon, will it have a greater or lower energy than a green photon?