23-5 The Hubble law relates the redshifts of remote galaxies to their distances from Earth
Whenever an astronomer finds an object in the sky that can be seen or photographed, the natural inclination is to attach a spectrograph to a telescope and record the spectrum. As long ago as 1914, Vesto M. Slipher, working at the Lowell Observatory in Arizona, began taking spectra of “spiral nebulae”—a name used before they were known to be galaxies. He was surprised to discover that of the 15 spiral nebulae he studied, the spectral lines of 11 were shifted toward the red end of the spectrum, indicating that they were moving away from Earth.
This marked dominance of redshifts over blueshifts was presented by Curtis in the 1920 Shapley-Curtis “debate” as evidence that these spiral nebulae could not be ordinary nebulae in our Milky Way Galaxy. It was only later that astronomers realized that the redshifts of spiral nebulae—that is, galaxies—reveal a basic law of our expanding universe.
Redshift, Distance, and the Hubble Law
The greater the redshift of a distant galaxy, the farther away it is
During the 1920s, Edwin Hubble and Milton Humason photographed the spectra of many galaxies with the 100-inch (2.5-meter) telescope on Mount Wilson in California. By observing the apparent brightnesses and pulsation periods of Cepheid variables in these galaxies, they were also able to measure the distance to each galaxy (see Section 23-2). Hubble and Humason found that most galaxies show a redshift in their spectrum. They also found a direct correlation between the distance to a galaxy and its redshift:
The more distant a galaxy, the greater its redshift and the more rapidly it is receding from us.
In other words, nearby galaxies are moving away from us slowly, and more distant galaxies are rushing away from us much more rapidly. Figure 23-16 shows this relationship for five representative elliptical galaxies. This universal recessional movement is referred to as the Hubble flow.
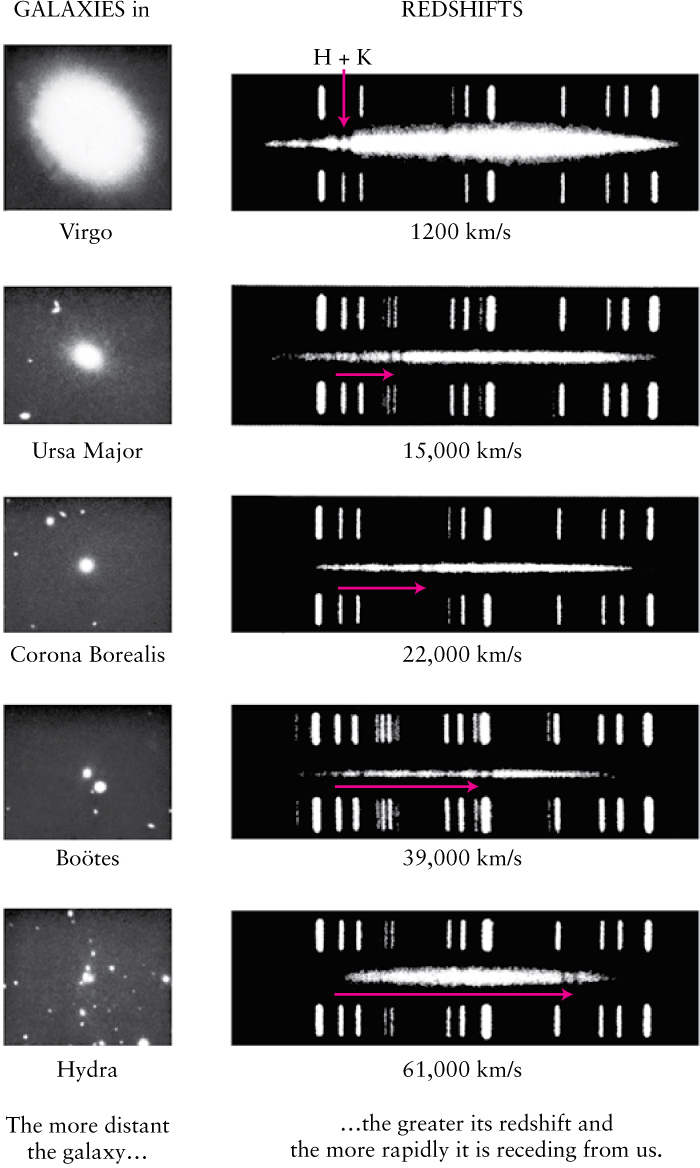
Relating the Distances and Redshifts of Galaxies These five galaxies are arranged, from top to bottom, in order of increasing distance from us. All are shown at the same magnification. Each galaxy’s spectrum is a bright band with dark absorption lines; the bright lines above and below it are a comparison spectrum of a light source at the observatory on Earth. The horizontal red arrows show how much the H and K lines of singly ionized calcium are redshifted in each galaxy’s spectrum. Below each spectrum is the recessional velocity calculated from the redshift. The more distant a galaxy is, the greater its redshift.
Hubble estimated the distances to a number of galaxies and the redshifts of those galaxies. The redshift, denoted by the symbol z, is found by taking the wavelength (λ) observed for a given spectral line, subtracting from it the ordinary, unshifted wavelength of that line (λ0) to get the wavelength difference (Δλ), and then dividing that difference by λ0:
Redshift of a receding object
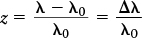
- z = redshift of an object
- λ0 = ordinary, unshifted wavelength of a spectral line
- λ = wavelength of that spectral line that is actually observed from the object
From the redshifts, Hubble used the Doppler formula to calculate the speed at which these galaxies are receding from us. Box 23-2 describes this calculation. Plotting the data on a graph of distance versus speed, Hubble found that the points lie near a straight line. Figure 23-17 is a modern version of Hubble’s graph based on recent data.
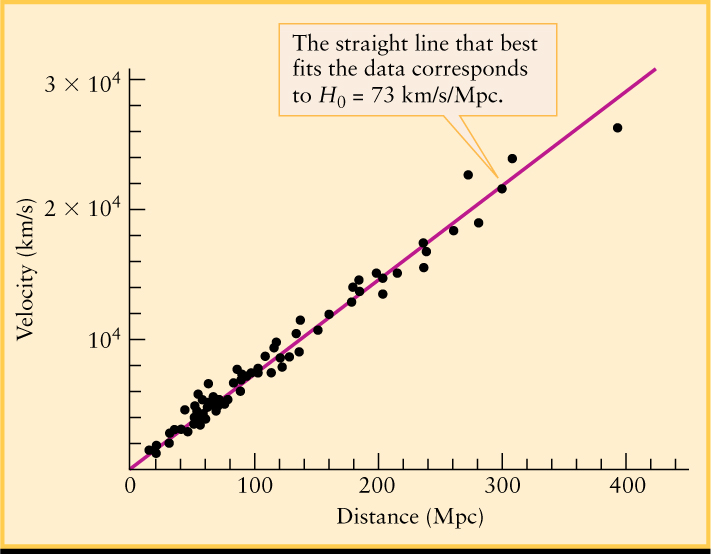
This relationship between the distances to galaxies and their redshifts was one of the most important astronomical discoveries of the twentieth century. As we will see in Chapter 26, this relationship tells us that we are living in an expanding universe. In 1929, Hubble published this discovery, which is now known as the Hubble law. The Hubble law is most easily stated as a formula:
The Hubble law
v = H0d
- v = recessional velocity of a galaxy
- H0 = Hubble constant
- d = distance to the galaxy
This formula is the equation for the straight line displayed in Figure 23-17, and the Hubble constant H0 is the slope of this straight line. From the data plotted on this graph we find that H0 = 73 km/s/Mpc (say “73 kilometers per second per megaparsec”). In other words, for each million parsecs to a galaxy, the galaxy’s speed away from us increases by 73 km/s. For example, a galaxy located 100 million parsecs from Earth should be rushing away from us with a speed of 7300 km/s. (In other books you may see the units of the Hubble constant written with exponents: 73 km s−1 Mpc−1.)
CAUTION!
A common misconception about the Hubble law is that all galaxies are moving away from the Milky Way. The reality is that galaxies have their own neighbor-induced motions relative to one another, due to their mutual gravitational attraction of neighboring galaxies. Astronomers call this neighbor-induced motion intrinsic velocity. For nearby galaxies, the speed of the Hubble flow is small compared to these intrinsic velocities. Hence, some of the nearest galaxies, including the Andromeda Galaxy (shown in Figure 23-3), are actually approaching us and have blueshifts rather than redshifts. But for distant galaxies, the Hubble speed v = H0d is much greater than any intrinsic motion that the galaxies might have. Even if the intrinsic velocity of such a distant galaxy is toward the Milky Way, the fast-moving Hubble flow sweeps that galaxy away from us.
BOX 23-2 TOOLS OF THE ASTRONOMER’S TRADE
The Hubble Law, Redshifts, and Recessional Velocities
Suppose that you aim a telescope at a distant galaxy. The galaxy will be moving away from you in the Hubble flow. You take a spectrum of the galaxy and find that the spectral lines are shifted toward the red end of the spectrum. For example, a particular spectral line whose normal wavelength is λ0 appears in the galaxy’s spectrum at a longer wavelength λ. The spectral line has thus been shifted by an amount Δλ = λ − λ0. The redshift of the galaxy, z, is given by
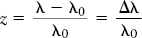
The redshift means that the galaxy is receding from us. According to the Hubble law, the recessional velocity v of a galaxy is related to its distance d from Earth by
v = H0d
where H0 is the Hubble constant. We can rewrite this equation

Given the value of H0, we can find the distance d to the galaxy if we know how to determine the recessional velocity v from the redshift z.
If the redshift is not too great (so that the redshift z is much less than 1), we can use the following Doppler shift equation to find the recessional speed:
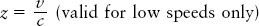
where c is the speed of light. For example, a 5% shift in wavelength (z = 0.05) corresponds to a recessional velocity of 5% of the speed of light (v = 0.05c).
For larger redshifts (around z = 0.1 or greater), a more complicated equation is needed to determine the recessional velocity. A small redshift can be explained by the Doppler shift as we have used here. However, as we will see in Chapter 25, larger redshifts arise from a large expansion of space and cannot be described as a simple Doppler shift. In fact, for galaxies at redshifts greater than about z > 1.5, recessional speeds exceed the speed of light. Due to the unique attributes of expanding space, faster-than-light recession is not a violation of Einstein’s laws.
EXAMPLE: When measured in a laboratory on Earth, the so-called K line of singly ionized calcium has a wavelength λ0 = 393.3 nm. But when you observe the spectrum of the giant elliptical galaxy NGC 4889, you find this spectral line at λ = 401.8 nm. Using H0 = 73 km/s/Mpc, find the distance to this galaxy.
Situation: We are given the values of λ and λ0 for a line in this galaxy’s spectrum. Our goal is to determine the galaxy’s distance d.
Tools: We use the relationship z = (λ − λ0)/λ0 to determine the redshift. We then use the appropriate formula to determine the galaxy’s recessional velocity v, and finally use the Hubble law to determine the distance to the galaxy.
Answer: The redshift of this galaxy is
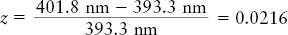
This value is substantially less than 0.1, so we can safely use the low-redshift relationship between recessional speed and redshift: v = zc. So NGC 4889 is moving away from us with a speed
v = zc = (0.0216)(3 × 105 km/s) = 6480 km/s
Using H0 = 73 km/s/Mpc in the Hubble law, the distance to this galaxy is

Review: This galaxy is receding from us at 0.0216 (2.16%) of the speed of light, and it is 89 megaparsecs (290 million light-years) away. Thus the light we see from NGC 4889 today left the galaxy 290 million years ago, even before the first dinosaurs appeared on Earth.
CONCEPT CHECK 23-9
In Figure 23-17, which follows Hubble’s law, consider galaxies at 100 Mpc and 200 Mpc. Which galaxy has the larger redshift?
From Figure 23-17, the farther away the galaxy, the larger its recessional velocity in the Hubble flow. Furthermore, a larger recessional velocity produces a larger redshift, so the farther galaxy has the largest redshift.
Pinning Down the Hubble Constant
A precise value of the Hubble constant has been a topic of heated debate among astronomers for several decades. The problem is that while redshifts are relatively easy to measure in a reliable way, distances to galaxies (especially remote galaxies) are not, as we saw in Section 23-4. Hence, astronomers who use different methods of determining galactic distances have obtained different values of H0. To see why different values are measured, it is helpful to rewrite the Hubble law as

This equation shows that if galaxies of a given recessional velocity (v) are far away (so d is large), the Hubble constant H0 must be relatively small. But if these galaxies are relatively close (so d is small), then H0 must have a larger value.
In the past, astronomers who used Type Ia supernovae for determining galactic distances found galaxies to be farther away than their colleagues who employed the Tully-Fisher relation. Therefore, the supernova adherents found values of H0 in the range from about 40 to 65 km/s/Mpc, while the values from the Tully-Fisher relation ranged from about 80 to 100 km/s/Mpc.
In the past few years, the Hubble Space Telescope has been used to observe Cepheid variables with unprecedented precision and in galaxies as far away as 30 Mpc (100 million ly). These observations and others suggest a value of the Hubble constant of about 73 km/s/Mpc, with an uncertainty of no more than 10%. At the same time, reanalysis of the supernova and Tully-Fisher results have brought the values of H0 from these techniques closer to the Hubble Space Telescope Cepheid value. We will adopt the value H0 = 73 km/s/Mpc in this book.
Determining the value of H0 has been an important task of astronomers for a very simple reason: The Hubble constant is one of the most important numbers in all astronomy. It expresses the rate at which the universe is expanding and, as we will see in Chapter 25, even helps give the age of the universe. Furthermore, the Hubble law can be used to determine the distances to extremely remote galaxies. If the redshift of a galaxy is known, the Hubble law can be used to determine its distance from Earth. Thus, the value of the Hubble constant helps determine the distances of the most remote objects in the universe that astronomers can observe.
Because the value of H0 remains somewhat uncertain, astronomers often express the distance to a remote galaxy simply in terms of its redshift z (which can be measured very accurately). Given the redshift, the distance to this galaxy can be calculated from the Hubble law, but the distance obtained in this way will depend on the particular value of H0 adopted. Rather than going through these calculations, an astronomer might simply say that a certain galaxy is “at z = 0.128.” From the Hubble law relating redshift and distance, this redshift makes it clear that the galaxy in question is more distant than one at z = 0.120 but not as distant as one at z = 0.130. When astronomers use redshift to describe distance, they are making use of the following general rule:
The greater the redshift of a distant galaxy, the greater its distance.
CONCEPT CHECK 23-10
Although nearly all distant galaxies have measureable redshifts, the relatively nearby Andromeda Galaxy exhibits an overall blueshift. What does this mean about the Andromeda Galaxy’s movement?
The spectral shift toward the shorter blue wavelengths means that the Andromeda Galaxy is moving toward our Milky Way Galaxy.
CALCULATION CHECK 23-1
What is the redshift z-value for a galaxy that has a galaxy spectral line shifted to 725.6 nm when a stationary object would emit the line at 656.3 nm?
Because z = the change in wavelength (λ − λ0) divided by the original λ0, z = (725.6 nm − 656.3 nm) ÷ 656.3 nm = 0.11.
CALCULATION CHECK 23-2
What is the distance to a galaxy that is observed to have a recessional velocity of 10,000 km/s?
Hubble’s Law, v = H0d, can be rearranged as d = v ÷ H0. Using H0 = 73 km/s/Mpc, d = v ÷ H0 = 10,000 km/s ÷ 73 km/s/Mpc = 134 Mpc (million parsecs).