25-6 The shape of the universe indicates its matter and energy content
We have seen that by following the mass densities of radiation (ρrad) and of matter (ρm), we can learn about the evolution of the universe. But it is equally important to know the combined mass density of all forms of matter and energy. (In an analogous way, an accountant needs to know the overall financial status of a company, not just individual profits or losses.) Remarkably, we can do this by investigating the overall shape of the universe.
The Curvature of the Universe
Einstein’s general theory of relativity explains that gravity curves the fabric of space. Furthermore, the equivalence between matter and energy, expressed by Einstein’s equation E = mc2, tells that either matter or energy produces gravity. Thus, the matter and energy scattered across space should give the universe an overall curvature. The degree of curvature depends on the combined average mass density of all forms of matter and energy. (Again, because of Einstein’s equivalence between matter and energy, some also refer to this as the combined average energy density.) This quantity, which we call ρ0 (say “rho sub zero”), is the sum of the average mass densities of matter, radiation, and any other form of energy. Thus, by measuring the curvature of space, we should be able to determine the value of ρ0 and, hence, learn about the content of the universe as a whole.
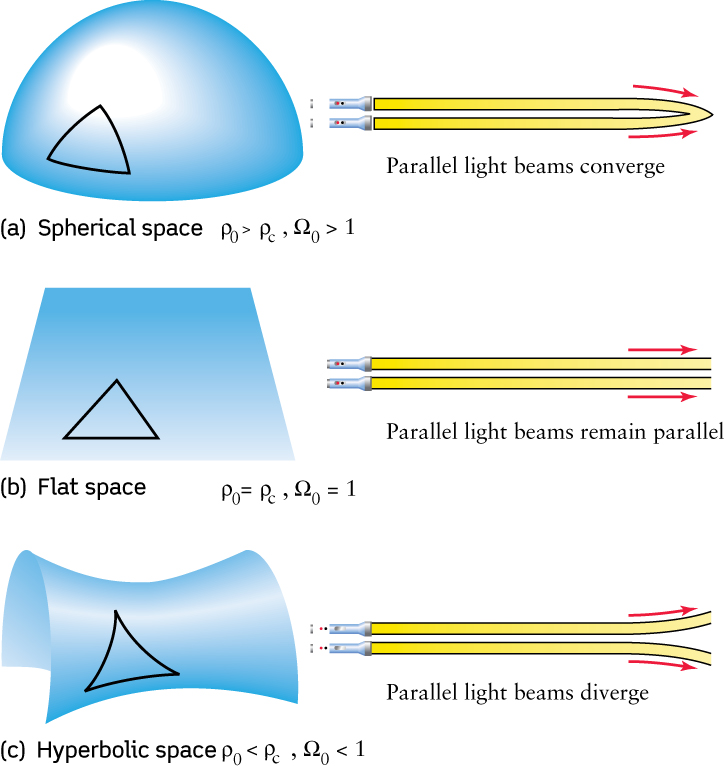
To see what astronomers mean by the curvature of the universe, imagine shining two powerful laser beams out into space so that they are perfectly parallel as they leave Earth. Furthermore, suppose that nothing gets in the way of these two beams, so we can follow them for billions of light-years as they travel across the universe and across the space whose curvature we wish to detect. Figure 25-14 illustrates the only three possibilities:
- We might find that our two beams of light remain perfectly parallel, even after traversing billions of light-years. In this case, space would not be curved: The universe would have zero curvature, and space would be flat.
- Alternatively, we might find that our two beams of light gradually converge. In such a case, space would not be flat. Recall that lines of longitude on Earth’s surface are parallel at the equator but intersect at the poles. Thus, in this case the three-dimensional geometry of the universe would be analogous to the two-dimensional geometry of a spherical surface. We would then say that space is spherical and that the universe has positive curvature. Such a universe is also called closed, because if you travel in a straight line in any direction in such a universe, you will eventually return to your starting point.
- Finally, we might find that the two initially parallel beams of light would gradually diverge, becoming farther and farther apart as they moved across the universe. In this case, the universe would still have to be curved, but in the opposite sense from the spherical model. We would then say that the universe has negative curvature. In the same way that a sphere is a positively curved two-dimensional surface, a saddle is a good example of a negatively curved two-dimensional surface. Parallel lines drawn on a sphere always converge, but parallel lines drawn on a saddle always diverge. Mathematicians say that saddle-shaped surfaces are hyperbolic. Thus, in a negatively curved universe, we would describe space as hyperbolic. Such a universe is also called open because if you were to travel in a straight line in any direction, you would never return to your starting point.
Figure 25-14 summarizes the three cases of positive curvature, zero curvature, and negative curvature. Real space is three-dimensional, but we have drawn the three cases as analogous, more easily visualized two-dimensional surfaces. Therefore, as you examine the drawings in Figure 25-14, remember that the real universe has one more dimension. For example, if the universe is in fact hyperbolic, then the geometry of space must be the (difficult to visualize) three-dimensional analog of the two-dimensional surface of a saddle.
Note that in accordance with the cosmological principle, none of these models of the universe has an “edge” or a “center.” This is clearly the case for both the flat and hyperbolic universes, because they are infinite and extend forever in all directions. A spherical universe is finite, but it also lacks a center and an edge. You could walk forever around the surface of a sphere (like the surface of Earth) without finding a center or an edge.
CONCEPT CHECK 25-11
If two lasers are aligned to be perfectly parallel out in a region of space far from any galaxies, could the geometry of space ever cause their light beams to cross?
Yes, as in Figure 25-14a. In a universe with the geometry of spherical space, parallel light beams will eventually cross. In this case, the universe is considered a closed space and has positive curvature.
Density Determines Curvature
The curvature of the universe is determined by the actual value of the combined mass density ρ0 and a reference density called the critical density ρc (say “rho sub cee”). If ρ0 is greater than the critical density ρc, the universe has positive curvature and is closed. If ρ0 is less than ρc, the universe has negative curvature and is open. In the special case that ρ0 is exactly equal to ρc, the universe is flat. Clearly, the critical density plays a crucial role in determining the geometry of the universe. It is given by the expression
Critical density of the universe
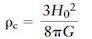
- ρc = critical density of the universe
- H0 = Hubble constant
- G = universal constant of gravitation
Using a Hubble constant H0 = 73 km/s/Mpc, we get
ρc = 1.0 × 10−26 kg/m3
This critical density amounts to only about 5 hydrogen atoms per cubic meter! Even with the vast empty spaces between the stars, this density is about a million times less than the density of matter from stars and gas in the disk in our Milky Way Galaxy.
Many astronomers prefer to characterize the combined average mass density of the universe in terms of the density parameter Ω0 (say “omega sub zero”). This parameter is just the ratio of the combined average mass density to the critical density:
Density parameter
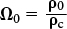
- Ω0 = density parameter
- ρ0 = combined average mass density
- ρc = critical density
An open universe (negative curvature) has a density parameter Ω0 between 0 and 1, and a closed universe (positive curvature) has Ω0 greater than 1. In a flat universe, Ω0 is equal to 1. Thus, we can use the value of Ω0 as a measure of the curvature of the universe (Table 25-1).
| Geometry of space | Curvature of space | Type of universe | Combined average mass density (ρ0) | Density parameter (Ω0) |
|---|---|---|---|---|
| Spherical | positive | closed | ρ0 > ρc | Ω0 > 1 |
| Flat | zero | flat | ρ0 = ρc | Ω0 = 1 |
| Hyperbolic | negative | open | ρ0 < ρc | Ω0 < 1 |
CALCULATION CHECK 25-3
What is the combined average mass density (in kg/m3) in a flat universe?
In a flat universe, Ω0 is equal to 1. That means ρ0 = (the combined average mass density) equals ρc = (the critical density). Therefore, ρ0 = 1.0 × 10−26 kg/m3.
Measuring the Cosmic Curvature
How can we determine the curvature of space across the universe? In theory, if you drew an enormous triangle whose sides were each a billion light-years long (see Figure 25-14), you could determine the curvature of space by measuring the three angles of the triangle. If their sum equaled 180°, space would be flat. If the sum was greater than 180°, space would be spherical. And if the sum of the three angles was less than 180°, space would be hyperbolic. Unfortunately, this direct method for measuring the curvature of space is not practical.
A way to determine the curvature of the universe that is both practical and precise is to see if light rays bend toward or away from each other, as shown in Figure 25-14. The greater the distance a pair of light rays has traveled, and hence, the longer the time the light has been in flight, the more pronounced any such bending should be. Therefore, astronomers test for the presence of such bending by examining the oldest radiation in the universe—the cosmic microwave background.
If the cosmic microwave background were truly isotropic, so that equal amounts of radiation reached us from all directions in the sky, it would be impossible to tell whether individual light rays have been bent. However, as we saw in Section 25-5, there are localized “hot spots” in the cosmic microwave background due to density variations in the early universe. The apparent size of these hot spots depends on the curvature of the universe (Figure 25-15). If the universe is closed, the bending of light rays from a hot spot will make the spot appear larger (Figure 25-15a); if the universe is open, the light rays will bend the other way and the hot spots will appear smaller (Figure 25-15c). Only in a flat universe will the light rays travel along straight lines, so that the hot spots appear with their true size (Figure 25-15b).

By calculating what conditions were like in the primordial fireball, astrophysicists find that in a flat universe, the dominant “hot spots” in the cosmic background radiation should have an angular size of about 1°. (In Section 25-9 we will learn how this is deduced.) This is just what observations of the CMB have confirmed (see Figure 25-13). Hence, the curvature of the universe must be very close to zero, and the universe must be either flat or very nearly so.
As Table 25-1 shows, once we know the curvature of the universe, we can determine the density parameter Ω0 and hence the combined average mass density ρ0. By analyzing the data shown in Figure 25-13, astrophysicists find that Ω0 = 1.0 with an uncertainty of about 2%. In other words, ρ0 is within 2% of the critical density ρc.
The flatness of the universe poses a major dilemma: Even if you include dark matter, there is not enough matter to make the universe flat. We saw in Section 25-5 that the average mass density of matter in the universe, ρm, is 2.4 × 10−27 kg/m3. This density is only 0.24 of the critical density ρc. We can express this ratio in terms of the matter density parameter Ωm (say “omega sub em”), equal to the ratio of ρm to the critical density:
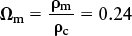
If matter and radiation were all there is in the universe, the combined average mass density ρ0 would be equal to ρm (plus a tiny contribution from radiation, which we can neglect because the average mass density of radiation is only about 0.02% that of matter). Then the density parameter Ω0 would be equal to Ωm—that is, equal to 0.24—and the universe would be open. But the temperature variations in the cosmic microwave background clearly show that the universe is either flat or very nearly so. These variations also show that the density parameter Ω0, which includes the effects of all kinds of matter and energy, is equal to 1.0. In other words, radiation and matter, including dark matter, together account for only 24% of the total density of the universe! The dilemma is to account for the rest of the density.
CONCEPT CHECK 25-12
In a closed universe, a 1-meter stick is moved from Earth out to a specific location in the distant cosmos. Assuming it could be observed from Earth, would the stick appear larger, smaller, or the same in size than in a flat universe at that same distance?
It would appear larger in size. As illustrated in Figure 25-15a, since the light rays are bent inward as they travel from the object toward an observer on Earth, the light rays appear to be coming from ends of the stick that are farther apart than as would be observed in a flat universe (Figure 25-15b). This makes the stick appear larger in the closed universe.
Dark Energy
The geometry of space reveals that the universe is filled with dark energy
The source of the missing energy density must be some form of energy that we cannot detect through the various gravitational effects that astronomers use to detect dark matter. The missing energy density also does not appear to emit detectable radiation of any kind, so we cannot directly detect it with light. With these properties in mind, we refer to this mysterious energy as dark energy.
Just as we express the average density of matter and radiation by the matter density parameter Ωm, we can express the average density of dark energy in terms of the dark energy density parameter ΩΛ (say “omega sub lambda”). This parameter is equal to the average mass density of dark energy, ρΛ, divided by the critical density ρc:
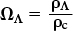
We can determine the value of ΩΛ by noting that the combined average mass density ρ0 must be the sum of the average mass densities of matter, radiation, and dark energy. As we have seen, the contribution of radiation is so small that we can ignore it, so we have
ρ0 = ρm + ρΛ
If we divide this through by the critical density ρc, we obtain
Ω0 = Ωm + ΩΛ
That is, the density parameter Ω0 is the sum of the matter density parameter Ωm and the dark energy density parameter ΩΛ. Solving for ΩΛ, we find
ΩΛ = Ω0 − Ωm
Since Ω0 is close to 1.0 and Ωm is 0.24, we conclude that ΩΛ must be 1.0 − 0.24 = 0.76. Thus, whatever dark energy is, it accounts for 76% (about three-quarters) of the energy content of the universe!
To put the dark energy density into context, consider the kinetic energy of a jumping flea. The flea’s kinetic energy is very small (about the same amount of electrical energy used in turning on a single LED light for one ten-millionth of a second). Since an energy density is the amount of energy contained within a certain volume, to put the dark energy density into context, we also need to indicate a corresponding volume. Thus, the dark energy density is equivalent to a single jumping flea within the volume of a big football stadium (dome and all). Since most of the universe is devoid of matter, this energy density, filling all of space, ends up being the dominant form of energy in our universe. (The CMB contains many photons, but the expansion of space has significantly lowered their energy and their density.)
The concept of dark energy is actually due to Einstein. When he proposed the existence of a cosmological constant, he was suggesting that the universe is filled with a form of energy that by itself tends to make the universe expand (see Section 25-1). Unlike gravity, which tends to make objects attract, the energy associated with a cosmological constant would provide a form of “antigravity.” Hence, it would not be detected in the same way as matter. (The subscript Λ in the symbol for the dark energy density parameter pays homage to the symbol that Einstein chose for the cosmological constant.)
If dark energy is in fact due to a cosmological constant, the value of this constant must be far larger than Einstein suggested. This change in the constant is needed if we are to explain why ΩΛ has a large value of 0.76. If Einstein felt he erred by introducing the idea of a cosmological constant, his error was giving it too small a value!
These ideas concerning dark energy are extraordinary, and extraordinary claims require extraordinary evidence to confirm them. As we will see in the next section, another way to measure dark energy is to examine how the rate of expansion of the universe has evolved over the eons.
CONCEPT CHECK 25-13
If we do not know what makes up dark energy, how can we estimate its energy density?
The total energy density of the universe determines whether the universe is open, closed, or flat. The cosmic microwave background reveals that the universe is nearly flat with Ω0 close to 1.0. Since matter can only account for about 0.24 of this energy density (and radiation is negligible), the remaining dark energy density is around 0.76.