25-5 The universe was a hot, opaque plasma during its first 380,000 years
Energy in the universe falls into one of two categories—radiation or matter. (We will encounter another type of energy in Section 25-7.) Photons are massless particles of light and are a form of radiation. There are many photons of starlight traveling across space, but the vast majority of photons in the universe are not visible and belong to the cosmic microwave background. The matter in the universe is contained in such luminous objects as stars, planets, and galaxies, as well as in nonluminous dark matter. A natural question to ask is which plays a more important role in the universe: radiation or matter? As we will see, the answer to this question is different for the early universe from the answer for our universe today.
Radiation and Matter in the Universe
To make a comparison between radiation and matter, recall Einstein’s famous equation E = mc2 (see Section 16-1). We can think of the photon energy in the universe (E) as being equal to a quantity of mass (m) multiplied by the square of the speed of light (c). The amount of this equivalent mass in a volume V, divided by that volume, is the mass density of radiation (ρrad; say “rho sub rad”).
We can combine E = mc2 with the Stefan-Boltzmann law (see Section 5-4) to give the following formula:
Mass density of radiation

- ρrad = mass density of radiation
- T = temperature of radiation
- σ = Stefan-Boltzmann constant = 5.67 × 10−8 W m−2 K−4
- c = speed of light = 3.00 × 108 m/s
For the present-day temperature of the cosmic background radiation, T = 2.725 K, this equation yields
ρrad = 4.6 × 10−31 kg/m3
The average density of matter (ρm; say “rho sub em”) in the universe is harder to determine. To find this density, we look at a large volume (V) of space, determine the total mass (M) of all the stars, galaxies, and dark matter in that volume, and divide the volume into the mass: ρm = M/V. (We emphasize that this quantity is the average density of matter. It would be the actual density if all the matter in the universe were spread out uniformly rather than being clumped into galaxies and clusters of galaxies.) Determining how much mass is in a large volume of space is a challenging task. A major part of the challenge involves dark matter, which emits no electromagnetic radiation and can be detected only by its gravitational influence (see Section 22-4 and Section 23-8).
One method that appears to deal successfully with this challenge is to observe clusters of galaxies, within which most of the luminous mass in the universe is concentrated and the contribution from dark matter can also be estimated. Rich clusters are surrounded by halos of hot, X-ray–emitting gas, typically at temperatures of 107 to 108 K (see Figure 23-26). Such a halo should be in hydrostatic equilibrium, so that it neither expands nor contracts but remains the same size (see Section 16-2, especially Figure 16-2). The outward gas pressure associated with the halo’s high temperature would then be balanced by the inward gravitational pull due to the total mass of the cluster. Thus, by measuring the temperature of the halo—which can be determined from the properties of the halo’s X-ray emission—astronomers can infer the cluster’s mass, including the contribution from dark matter!
From galaxy clusters and other measurements, the present-day average density of matter in the universe is estimated to be
ρm = 2.4 × 10−27 kg/m3
with an uncertainty of about 15%. The mass of a single hydrogen atom is 1.67 × 10−27 kg. Hence, if the mass of the universe were spread uniformly over space, there would be the equivalent of 1½ hydrogen atoms per cubic meter of space. By contrast, there are 5 × 1025 atoms in a cubic meter of the air you breathe! The very small value of ρm shows that our universe has a very low average density.
Furthermore, by counting galaxies and other measurements, astronomers determine that the average density of luminous matter (that is, the stars and gas within clusters of galaxies) is about 4.2 × 10−28 kg/m3. This density is only about 17% of the average density of matter of all forms. Thus, nonluminous dark matter is actually the predominant form of matter in our universe. The “ordinary” matter (protons and neutrons) of which the stars, the planets, and ourselves are made is only about one-fifth of the total matter!
The fact that there is more dark matter than regular matter does not make it any easier to detect. By interacting with light, regular matter can cool and condense into stars and planets. However, dark matter is more evenly and sparsely distributed. The actual amount of dark matter within Earth’s volume at any given time is only about 1 kg. It is thought that dark matter particles stream right through the Earth with only rare interactions. Due to its elusive nature, yet dominance over regular matter, the detection of dark matter particles is considered one of the “Holy Grails” of physics and astronomy and would surely result in a Nobel Prize.
When Radiation Held Sway Over Matter
Although the average density of matter in the universe is tiny by Earth standards, it is thousands of times larger than ρrad, the mass density of radiation. However, this ratio was not always the case. Matter prevails over radiation today only because the energy now carried by microwave photons is so small. Nevertheless, the number of photons in the microwave background is astounding. From the physics of blackbody radiation it can be calculated that there are today 410 million (4.1 × 108) photons in every cubic meter of space. In other words, the photons in space outnumber atoms by roughly a billion (109) to one. In terms of total number of particles, the universe thus consists almost entirely of microwave photons. This radiation field no longer has much effect on the universe however, because its photons have been redshifted to long wavelengths and low energies after 13.7 billion years of being stretched by the expansion of the universe.
In contrast, think back toward the Big Bang. The universe becomes increasingly compressed, and thus the density of matter increases as we go back in time. The photons in the background radiation also become more crowded together as we go back in time. But, in addition, the photons become less redshifted and thus have shorter wavelengths and higher energy than they do today. Because of this added energy, the mass density of radiation (ρrad) increases more quickly as we go back in time than does the average density of matter (ρm). In fact, as Figure 25-10 shows, there was a time in the ancient past when ρrad equaled ρm. Before this time, ρrad was greater than ρm, and radiation thus held sway over matter. Astronomers call this state a radiation-dominated universe. After ρm became greater than ρrad, so that matter prevailed over radiation, our universe became a matter-dominated universe.

The temperature of the background radiation has declined over the eons thanks to the expansion of the universe
This transition from a radiation-dominated universe to a matter-dominated universe occurred about 24,000 years after the Big Bang, at a time that corresponds to a redshift of about z = 5200. Since that time the wavelengths of photons have been stretched by a factor of 1 + z, or about 5200. Today these microwave photons typically have wavelengths of about 1 mm. But when the universe was about 24,000 years old, they had wavelengths of about 190 nm in the ultraviolet part of the spectrum.
To calculate the temperature of the cosmic background radiation at the time of this transition from a radiation-dominated universe to a matter-dominated one, we use Wien’s law (see Section 5-4). This law says that the wavelength of maximum emission (ρmax) of a blackbody is inversely proportional to its temperature (T): A decrease of ρmax by a factor of 2 corresponds to an increase of T by a factor of 2.
The present-day peak wavelength of the cosmic background radiation corresponds to a blackbody temperature of 2.725 K. Hence, a peak wavelength 5200 times smaller corresponds to a temperature 5200 times greater: T = 5200 × 2.725 K = 14,000 K. In other words, the radiation temperature at redshift z was greater than the present-day radiation temperature by a factor of 1 + z. Therefore, the temperature of the radiation background was once much greater and has been declining over the ages, as Figure 25-11 shows.

CONCEPT CHECK 25-8
At the time Earth formed, was the universe dominated by energy or by matter?
Earth formed about 4.5 billion years ago, when the universe was about 9 billion years old, and the universe has been dominated by matter for most of its history.
When the First Atoms Formed
The nature of the universe changed again in a fundamental way about 380,000 years after the Big Bang, when z was roughly 1100 and the temperature of the radiation background was about 1100 × 2.725 K = 3000 K. (At a temperature of 3000 K, the entire universe was filled with visible orange light.) To see the significance of this moment in cosmic history, recall that hydrogen is by far the most abundant element in the universe—hydrogen atoms outnumber helium atoms by about 12 to 1. A hydrogen atom consists of a single proton orbited by a single electron, and it takes relatively little energy to knock the electron completely out of its orbit around the proton. In fact, ultraviolet radiation warmer than about 3000 K easily ionizes hydrogen. Thus, neutral hydrogen atoms could not survive in the universe that existed before z = 1100. That is, in the first 380,000 years after the Big Bang, the background photons had energies great enough to prevent electrons and protons from binding to form hydrogen atoms (Figure 25-12a). Only since z = 1100 (that is, since t = 380,000 years) have the energies of these photons been low enough to permit hydrogen atoms to exist (Figure 25-12b).
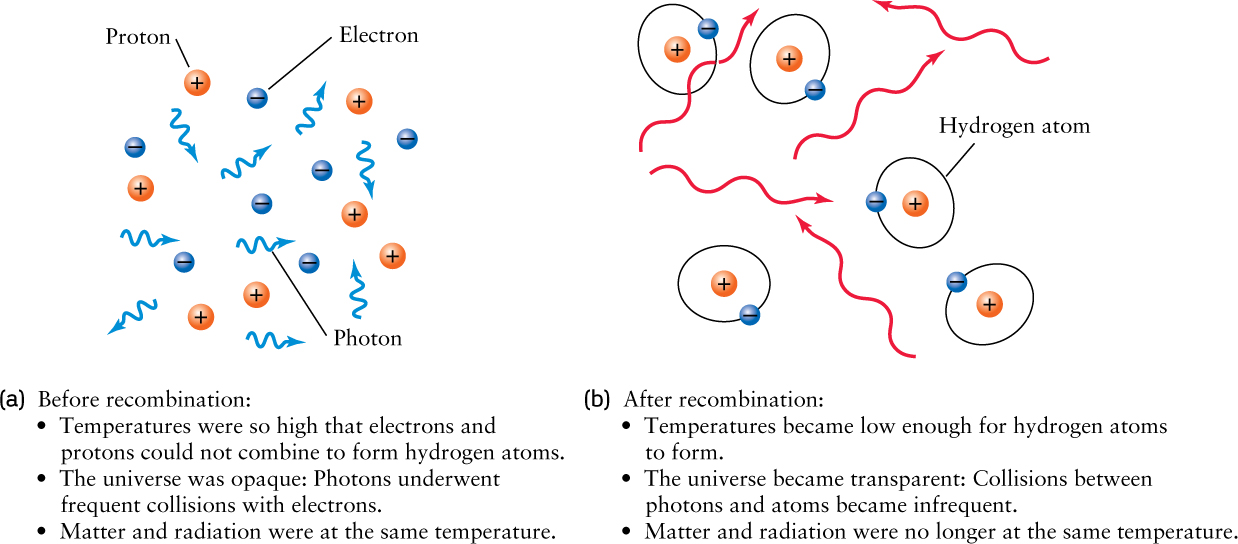
The epoch when atoms first formed at t = 380,000 years is called the era of recombination. This name refers to electrons “recombining” to form atoms. (The name is a bit misleading, because the electrons and protons had never before combined into atoms.)
Prior to t = 380,000 years, the universe was completely filled with a shimmering expanse of high-energy photons colliding vigorously with protons and electrons. This state of matter, called a plasma, is opaque, which means that light cannot pass through it without being strongly scattered and absorbed. The surface and interior of the Sun are also a hot, glowing, opaque plasma (see Section 16-9). P. J. E. Peebles coined the term primordial fireball to describe the universe during its first 380,000 years of existence.
After t = 380,000 years, the photons no longer had enough energy to keep the protons and electrons apart. As soon as the temperature of the radiation field fell below about 3000 K, protons and electrons began combining to form hydrogen atoms. These atoms do not absorb low-energy photons, so space became transparent! All the photons that heretofore had been vigorously colliding with charged particles could now stream unimpeded across space. Today, these same photons constitute the microwave background.
The significance of the era of recombination becomes clear by considering how it affects an astronomer’s ability to form images of the early universe. After recombination, the photons from a large clump of matter can stream to us while having very little interaction with the matter they pass through along their journey. These undisturbed photons can carry images of different clumps of matter in the early universe. On the other hand, photons emitted prior to recombination are scattered so strongly that any image from that early time is completely blurred out before its photons reach us. Therefore, the era of recombination marks the earliest time and farthest distance that astronomers can collect images of the universe.
Before recombination, matter and the radiation field had the same temperature, because photons, electrons, and protons were all in continuous interaction with one another. After recombination, photons and atoms hardly interacted at all, and thus the temperature of matter in the universe was no longer the same as the temperature of the background radiation. Thus, T = 2.725 K is the temperature of the present-day background radiation field, not the temperature of the matter in the universe. Note that while the temperature of the background radiation is very uniform, the temperature of matter in the universe is anything but: It ranges from hundreds of millions of kelvins in the interiors of giant stars to a few tens of kelvins in the interstellar medium.
ANALOGY
A good analogy is the behavior of a glass of cold water. If you hold the glass in your hand, the water will get warmer and your hand will get colder until both the water and your hand are at the same temperature. But if you set the glass down and do not touch it, so that the glass and your hand do not interact, their temperatures are decoupled: The water will stay cold and your hand will stay warm for much longer.
Because the universe was opaque prior to t = 380,000 years, we cannot see any further into the past than the era of recombination. In particular, we cannot see back to the era when the universe was radiation-dominated. The microwave background, whose photons have suffered a redshift of z = 1100, contains the most ancient photons we will ever be able to observe.
CONCEPT CHECK 25-9
If the universe had cooled more slowly, would the first atoms have appeared more quickly or more slowly?
The universe had to be sufficiently cool for atoms to form, so if the early universe was hotter for longer, the first atoms would have appeared more slowly.
Nonuniformities in the Early Universe and the Origin of Galaxies
The COBE data show that the universe is full of blackbody radiation with a temperature of 2.725 K. (This is the cosmic microwave background radiation, or CMB, discussed in Section 25-4.) However, more sensitive observations show that there are slight temperature variations spread across the sky (Figure 25-13). What do these temperature variations tell us?
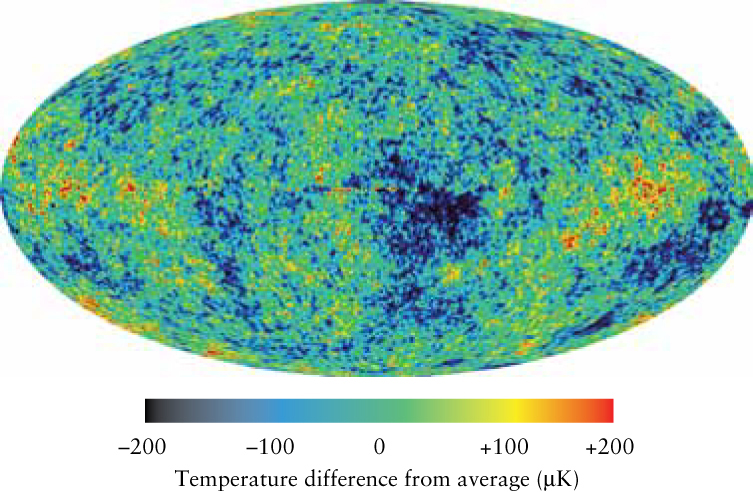

 Temperature Variations in the Cosmic Microwave Background This map from WMAP data shows small variations in the temperature of the cosmic background radiation across the entire sky. (The variations due to Earth’s motions through space, shown in Figure 25-8, have been factored out.) Lower-temperature regions (shown in blue) show where the early universe was slightly denser than average; warmer regions (shown in red) correspond to regions where the density of matter was less dense than average. Note that the temperature variations in this figure are no more than 200 μK, or 2 × 10−4 K; these are tiny fluctuations around the blackbody radiation measured by COBE in Figure 25-7.
Temperature Variations in the Cosmic Microwave Background This map from WMAP data shows small variations in the temperature of the cosmic background radiation across the entire sky. (The variations due to Earth’s motions through space, shown in Figure 25-8, have been factored out.) Lower-temperature regions (shown in blue) show where the early universe was slightly denser than average; warmer regions (shown in red) correspond to regions where the density of matter was less dense than average. Note that the temperature variations in this figure are no more than 200 μK, or 2 × 10−4 K; these are tiny fluctuations around the blackbody radiation measured by COBE in Figure 25-7.
The distribution of matter in the early universe was not perfectly uniform, and these temperature variations reveal the nonuniformities—the clumps and voids—in the mass distribution. It is important to understand that the temperature fluctuations do not arise from the temperature of the matter. Instead, clumps in the distribution of matter produce a gravitational redshift (see Figure 21-7b) on the CMB photons as they leave a denser region. Redshifted CMB photons not only have longer wavelengths and lower energy, but also correspond to lower CMB temperatures. Thus, in Figure 25-13, the cooler bluer spots correspond to denser regions.
Astronomers place great importance on studying temperature and density variations in the cosmic background radiation. The reason is that clumps of matter seen at early times are the “seeds” of structures that continued to “grow” into today’s superclusters of galaxies through gravitational contraction. Within these immense concentrations formed the galaxies, stars, and planets. Thus, by studying these nonuniformities, we are really studying the origins of our present-day structure.
Temperature variations in the cosmic background radiation do more than show us the origins of large-scale structure in the universe. As we will see in the next two sections, these temperature variations actually reveal the shape of the universe as a whole, and many of its most fundamental properties.
CONCEPT CHECK 25-10
Consider a blue patch in Figure 25-13. If astronomers looked at the same region with a visible-light telescope, what are they likely to see?
Cooler blue regions correspond to denser concentrations of mass in the early universe. These are often the seeds of structures that form later in that same region. A visible-light telescope would probably find a supercluster of galaxies in that same region.