22-4 The rotation of our Galaxy reveals the presence of dark matter
The Doppler shifts observed in the disk of our Galaxy tell us that the disk rotates. This rotation shows that the stars, gas, and dust in our Galaxy are all orbiting the galactic center. Indeed, if this were not the case, mutual gravitational attraction would cause the entire Galaxy to collapse into the galactic center. In the same way, the Moon is kept from crashing into Earth and the planets from crashing into the Moon because of their orbital motion (see Section 4-7).
Measuring the rotation of our Galaxy accurately is a difficult business. But such challenging measurements have been made, as we shall see, and the results led to a remarkable conclusion: Most of the mass of the Galaxy is in the form of dark matter, a mysterious sort of material that emits no light at all.
Measuring How the Milky Way Rotates
Radio observations of 21-cm radiation from hydrogen gas provide important clues about our Galaxy’s rotation. Doppler shift measurements of this radiation indicate that stars and gas all orbit in the same direction around the galactic center, just as the planets all orbit in the same direction around the Sun.
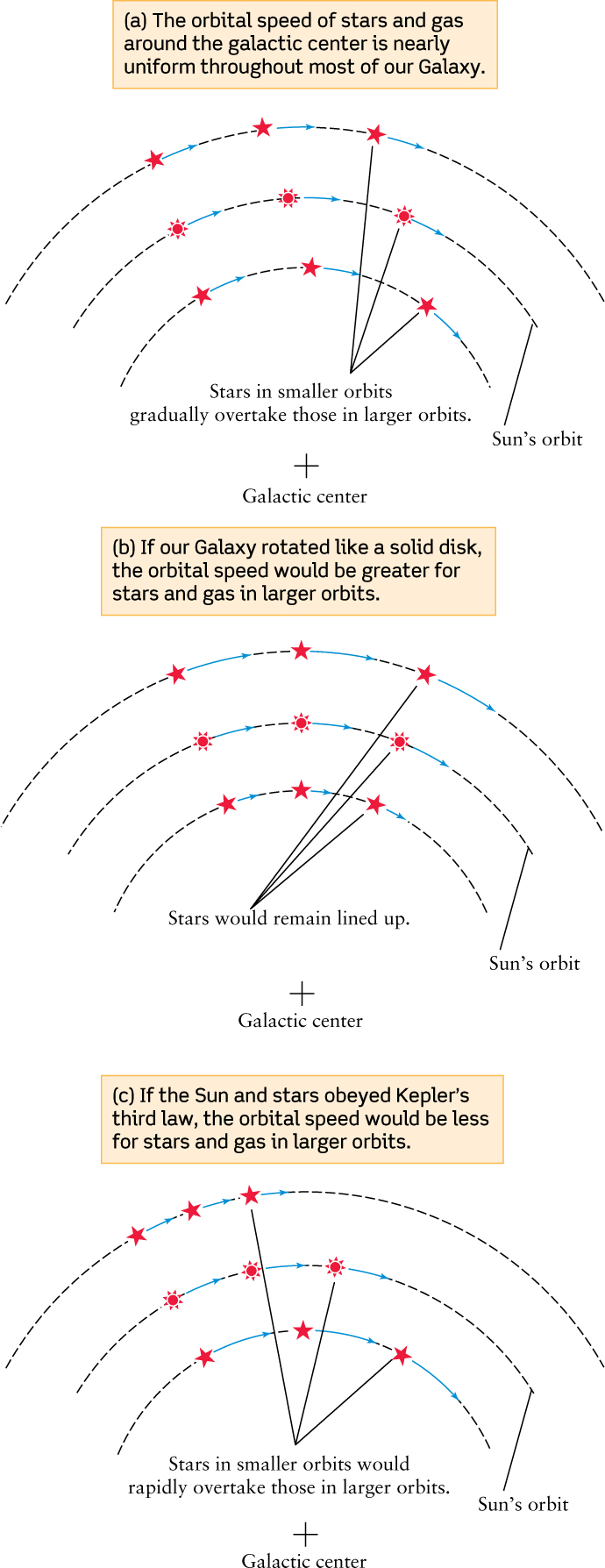
Measurements also show that the orbital speed of stars and gas around the galactic center is fairly uniform throughout much of the Galaxy’s disk (Figure 22-17). As a result, stars orbiting between the Sun and the galactic center complete a trip around the galactic center more quickly than the Sun, because the stars have a shorter distance to travel. Conversely, stars outside the Sun’s orbit take longer to go once around the galactic center because they have farther to travel. As seen by Earth-based astronomers moving along with the Sun, stars inside the Sun’s orbit overtake and pass us, while we overtake and pass stars outside the Sun’s orbit (Figure 22-17a).
CAUTION!
Note that when we say that objects in different parts of the Galaxy orbit at the same speed, we do not mean that the Galaxy rotates like a solid disk. All parts of a rotating solid disk—a CD or DVD, for example—take the same time to complete one rotation. Because the outer part of the disk has to travel around a larger circle than the inner part, the speed (distance per time) is greater in the outer part (Figure 22-17b). By contrast, the orbital speed of material in our Galaxy is roughly the same at all distances from the galactic center.
The most familiar examples of orbital motion are the motions of the planets around the Sun. As we saw in Section 4-7, the farther a planet is from the Sun, the less gravitational force it experiences and the slower the speed it needs to have to remain in orbit. The same would be true for the orbits of stars and gas in the Galaxy if they were held in orbit by a single, massive object at the galactic center (see Figure 22-17c). Hence, the 21-cm H I wavelength observations of our Galaxy, which show that the speed of orbiting objects does not decrease with increasing distance from the galactic center, demonstrate that there is no such single, massive object holding objects in their galactic orbits.
Instead, what keeps a star in its orbit around the center of the Galaxy is the combined gravitational force exerted on it by all of the mass (including stars, gas, and dust) that lies within the star’s orbit. (It turns out that the gravitational force from matter outside a star’s orbit balances out and has little or no net effect on the star’s motion around the galactic center.) This gives us a tool for determining the Galaxy’s mass and how that mass is distributed.
CONCEPT CHECK 22-8
Which would have a greater impact on changing the length of time it takes the Sun to orbit the galactic center—adding more stars to the galactic center or adding more stars to the galactic halo?
The most important factor for how fast a star moves around the galaxy is how much mass is closer to the galactic center than the star.
The Sun’s Orbital Motion and the Mass of the Galaxy
An important example is the orbital motion of the Sun (and the solar system) around the center of the Galaxy. If we know the semimajor axis and period of the Sun’s orbit, we can use Newton’s form of Kepler’s third law (described in Section 4-7) to determine the mass of that portion of the Galaxy that lies within the orbit. We saw in Section 22-2 that the Sun is about 8000 pc (26,000 ly) from the galactic center. The orbit is in fact nearly circular, so we can regard 8000 pc as the radius r of the orbit. (This radius is also the semimajor axis of the Sun’s orbit.) In one complete trip around the Galaxy, the Sun travels a distance equal to the circumference of its orbit, which is 2πr. The time required for one orbit, or orbital period P, is equal to the distance traveled divided by the Sun’s orbital speed v:
Period of the Sun’s orbit around the galactic center
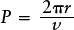
- P = orbital period of the Sun
- r = distance from the Sun to the galactic center
- v = orbital speed of the Sun
Unfortunately, we cannot tell the Sun’s orbital speed from 21-cm observations, because these reveal only how fast things are moving relative to the Sun. Instead, we need to measure how the Sun is moving relative to a background that is not rotating along with the rest of the Galaxy. Such a background is provided by distant galaxies beyond the Milky Way and by the globular clusters. (Since globular clusters lie outside the plane of the Milky Way, they do not take part in the rotation of our Galaxy’s disk.) By measuring the Doppler shifts of these objects and averaging their velocities, astronomers deduce that the Sun is moving along its orbit around the galactic center at about 220 km/s—about 790,000 kilometers per hour or 490,000 miles per hour!
Using this information, we find that the Sun’s orbital period is
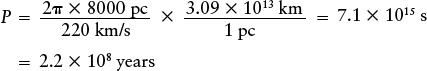
Traveling at 790,000 kilometers per hour, it takes the Sun about 220 million years to complete one trip around the Galaxy. (In the 65 million years since the demise of the dinosaurs, our solar system has traveled less than a third of the way around its orbit.) The Galaxy is a very large place!
Box 22-2 shows how to combine the radius and period of the Sun’s orbit to calculate the total mass of all the matter that lies inside the Sun’s orbit. Such calculations give an answer of 9.0 × 1010 M⊙ (90 billion solar masses). As Figure 22-7 shows, the Galaxy extends well beyond the Sun’s orbit, so the mass of the entire Galaxy must be larger than this mass.
BOX 22-2 TOOLS OF THE ASTRONOMER’S TRADE
Estimating the Mass Inside the Sun’s Orbit
The force that keeps the Sun in orbit around the center of the Galaxy is the gravitational pull of all the matter interior to the Sun’s orbit—this force is described by Newton’s law of gravity. We can estimate the total mass of all of this matter using Newton’s form of Kepler’s third law (see Section 4-7 and Box 4-4):
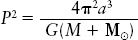
In this equation P is the orbital period of the Sun, a is the semimajor axis of the Sun’s orbit around the galactic center, G is the universal constant of gravitation, M is the amount of mass inside the Sun’s orbit, and M⊙ is the mass of the Sun.
Because the Sun is only one of more than 1011 stars in the Galaxy, the Sun’s mass is minuscule compared to M. Hence, we can safely replace the sum M + M⊙ in the above equation with just M. If we now assume that the Sun’s orbit is a circle, the semimajor axis a of the orbit is just the radius of this circle, which we call r. The period P of the orbit is equal to 2πr/v, where v is the Sun’s orbital speed. You can then show that
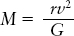
(We leave the derivation of this equation as an exercise at the end of this chapter.)
Now we can insert known values to obtain the mass inside the Sun’s orbit. Being careful to express distance in meters and speed in meters per second, we have v = 220 km/s = 2.2 × 105 m/s, G = 6.67 × 10−11 newton ∙ m2/kg2, and

Hence, we find that

or, in terms of the mass of the Sun,
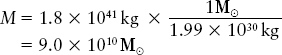
This estimate involves only mass that is interior to the Sun’s orbit. Matter outside the Sun’s orbit has no net gravitational effect on the Sun’s motion and thus does not enter into Kepler’s third law. (This is strictly true only if the matter outside our orbit is distributed over a sphere rather than a disk. In fact, the dark matter that dominates our Galaxy seems to have a spherical distribution.)
CALCULATION CHECK 22-2
Since it formed 4.5 billion years ago, how many orbits around the Galaxy has the Sun made?
Remembering that it takes 2.2 × 108 years for the Sun to make one orbit around the Galaxy, 4.5 × 109 years × (1 orbit/2.2 × 108 years) = 20 orbits.
Rotation Curves and the Mystery of Dark Matter
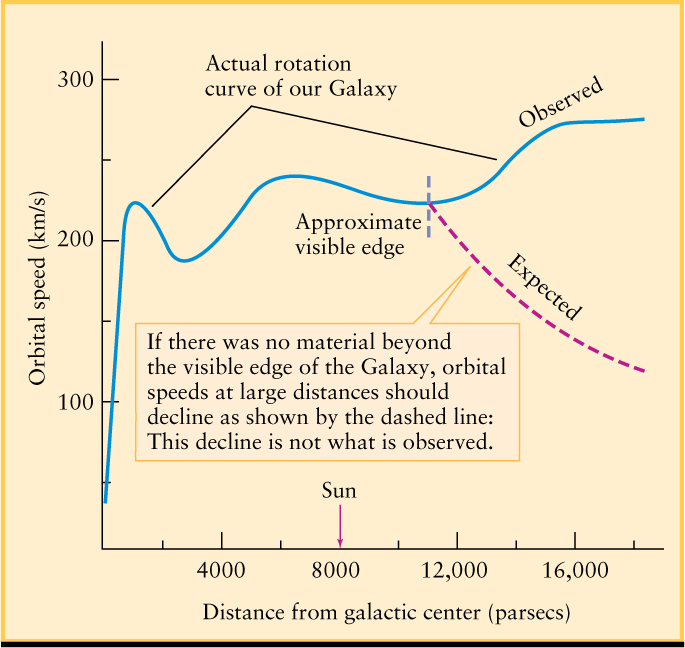
In recent years, astronomers have been astonished to discover how much matter may lie outside the Sun’s orbit. The clues come from 21-cm radiation emitted by hydrogen in spiral arms that extend to the outer reaches of the Galaxy. Because we know the true speed of the Sun, we can convert the Doppler shifts of this radiation into actual speeds for the spiral arms. This calculation gives us a rotation curve, a graph of the speeds of galactic rotation measured outward from the galactic center (Figure 22-18). We would expect that for gas clouds beyond the confines of most of the Galaxy’s mass, the orbital speed should decrease with increasing distance from the Galaxy’s center, just as the orbital speeds of the planets decrease with increasing distance from the Sun (see Figure 22-17c). But as Figure 22-18 shows, the Galaxy’s rotation curve is quite flat, indicating roughly uniform orbital speeds well beyond the visible edge of the galactic disk.
Unlike the Galaxy’s stars and dust, its dark matter forms a roughly spherical halo
To explain these nearly uniform orbital speeds in the outer parts of the Galaxy, astronomers conclude that a large amount of matter must lie outside the Sun’s orbit. When this matter is included, the total mass of our Galaxy could exceed 1012 M⊙ or more, of which about 10% is in the form of stars. This percentage implies that our Galaxy contains roughly 200 billion stars.
These observations lead to a profound mystery. Stars, gas, and dust account for only about 10% of the Galaxy’s total mass. What, then, makes up the remaining 90% of the matter in our Galaxy? Whatever it’s made of, it’s dark. It does not show up on photographs nor indeed in images made in any part of the electromagnetic spectrum. This unseen material, which is by far the predominant constituent of our Galaxy, is called dark matter. We sense its presence only through its gravitational influence on the orbits of stars and gas clouds.
CAUTION!
Be careful not to confuse dark matter with dark nebulae. A dark nebula like the one in Figure 18-4 emits no visible light, but does radiate at longer wavelengths. By contrast, no electromagnetic radiation of any kind has yet been discovered coming from dark matter.
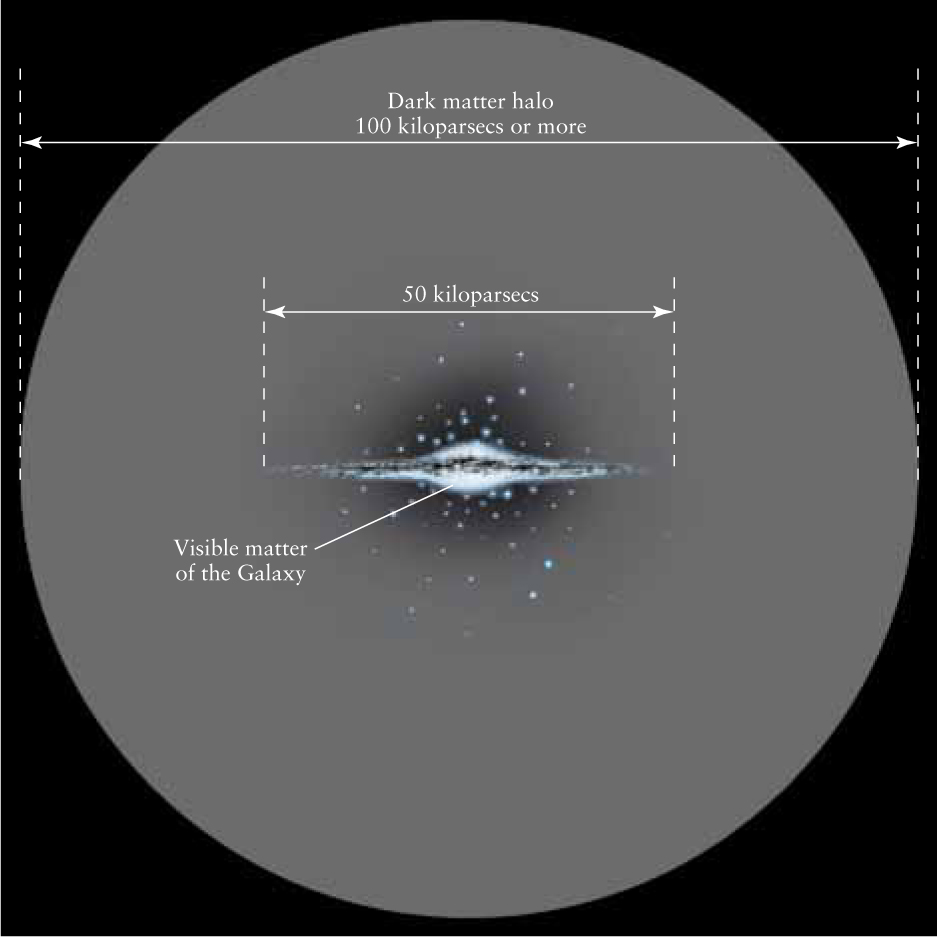
Observations of star groupings outside the Milky Way suggest that our Galaxy’s dark matter forms a spherical halo, with the galactic nucleus at its center, like the halo stars and globular clusters shown in Figure 22-7. However, the dark matter halo is much larger; it may extend to a distance of 100–200 kpc from the center of our Galaxy, some 2 to 4 times the extent of the visible halo (Figure 22-19). Analysis of the rotation curve in Figure 22-18 shows that the density of the dark matter halo decreases with increasing distance from the center of the Galaxy.
CONCEPT CHECK 22-9
How would the motion of stars at the edge of our Galaxy be different if there were no dark matter present?
In the absence of dark matter, the stars most distant from the galactic center should be moving much slower than those stars orbiting closer to the center.
Dark Matter Speculations
What is the nature of this mysterious dark matter? One proposal is that the dark matter halo is composed, at least in part, of dim objects with masses less than 1 M⊙. These objects, which could include brown dwarfs, white dwarfs, or black holes, are called massive compact halo objects, or MACHOs. While some brown dwarfs and white dwarfs emit measurable light, it is possible that many more are simply too dim to detect, making them candidates for dark matter. Astronomers have searched for MACHOs by monitoring the light from distant stars. If a MACHO passes between us and the star, its gravity will bend the light coming from the star. (In Section 23-2 we describe how gravity can bend starlight.) As Figure 22-20 shows, the MACHO’s gravity acts like a lens that focuses the light from the star. This effect, called microlensing, makes the star appear to brighten substantially for a few days.

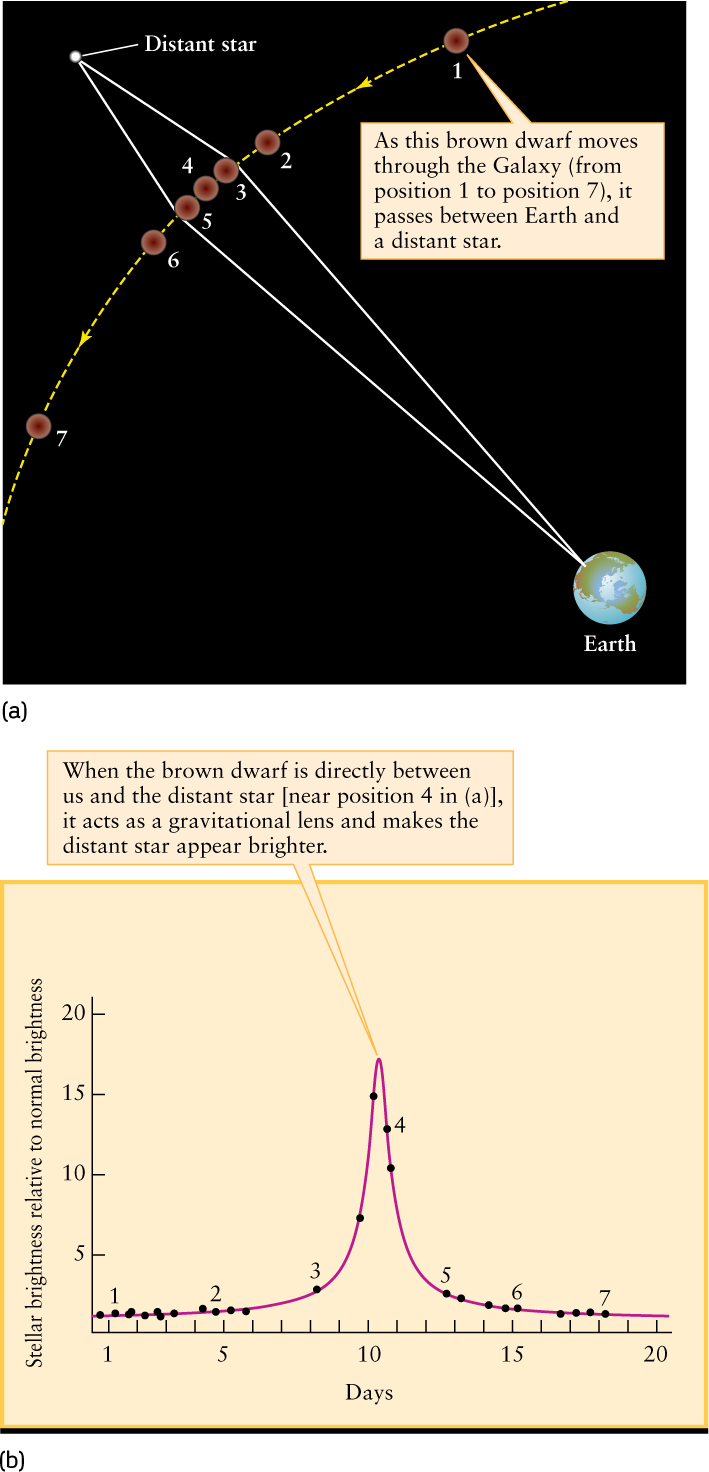
Astronomers have indeed detected MACHOs in this way, but not nearly enough to solve the dark matter mystery. MACHOs with very low mass (10−6 to 0.1 M⊙ each) do not appear to be a significant part of the dark matter halo. MACHOs of roughly 0.5 M⊙ are more prevalent, but account for less than 10% of the dark matter halo.
The remainder of the dark matter is thought to be more exotic than the regular atoms (consisting of electrons, protons, and neutrons) that make up known astrophysical objects. One idea proposed for dark matter is the neutrino. As we saw in Section 16-4, one type of neutrino can transform into another, and these transformations can only take place if neutrinos have mass. While we do not yet know what masses the neutrinos have, we have come to understand that they are unlikely to account for halo dark matter. As we will see in Chapter 26 (Section 26-6), fast-moving neutrinos cannot “clump” enough to form a halo around our Galaxy. The remainder of the dark matter is thought to be much more exotic.
Another possibility that has been proposed is a new class of subatomic particles called weakly interacting massive particles, or WIMPs. These particles are suggested by certain theories that have not yet been confirmed experimentally. In these theories, WIMPS do not emit or absorb light (neither visible light nor any other electromagnetic radiation), but interact with regular matter through the same “weak” force that neutrinos do.
A billion or so WIMPs might be passing through you each second (compared to a trillion or so neutrinos). While dark matter makes up 90% of the matter in our Galaxy, dark matter particles, such as WIMPs, would be spread out much more than regular matter. In fact, the amount of dark matter passing through Earth at any given time would only be about 1 kg!
Physicists are attempting to detect these curious particles, which would have masses 10 to 10,000 times greater than a proton or neutron, by using a large crystal cooled almost to absolute zero. If a WIMP should enter this crystal and collide with one of its atoms, the collision will deposit a tiny but measurable amount of heat in the crystal.
Another approach for detecting WIMPs searches for the light (and electrons) that are produced after the WIMPs collide with xenon atoms. One such experiment that began collecting data in 2013 is called LUX and is at the bottom of the Homestake Mine in South Dakota (Figure 22-21). The earth above the experiment shields out unwanted particles coming in from space, while the WIMPs should easily pass through toward the xenon-filled detector. With WIMPs as the main hypothesis for dark matter, even larger experiments are being built for their discovery.
As yet, the true nature of dark matter remains a mystery. Furthermore, this mystery is not confined to our own Galaxy. In Chapter 23 we will find that other galaxies have the same sort of rotation curve as in Figure 22-18, indicating that they also contain vast amounts of dark matter. Indeed, dark matter appears to make up most of the mass in our universe. Hence, dark matter is one of the most important unsolved problems in physics and astronomy.
CONCEPT CHECK 22-10
If MACHOs have been observed but WIMPs have not, why do you suppose scientists think that most of dark matter might come from WIMPs?
Astronomers detected only a small amount of matter in the form of MACHOs, yet they would have detected more if it were there. Therefore, the source of dark matter still remains to be discovered. Until WIMPs are detected, or ruled out, they remain a good candidate.