26-1 The newborn universe underwent a brief period of vigorous expansion
With the discovery of the cosmic microwave background, astronomers had direct evidence that the universe began with a hot Big Bang (see Section 25-4). Remarkably, the microwave background is incredibly uniform, or isotropic, across the sky. If we subtract the effects of our own motion through the microwave background (see Figure 25-8), we find that the temperature of the microwave background is the same in all parts of the sky with deviations typically less than 0.01%. These small deviations, or nonuniformities, in the microwave background are also remarkable, in part because their angular sizes help indicate that our universe has a flat geometry (see Section 25-6, especially Figure 25-16). As striking as these observations are, they pose substantial challenges to the standard theory of the expansion of the universe.
The Isotropy Problem: Why Is the Microwave Background So Uniform?
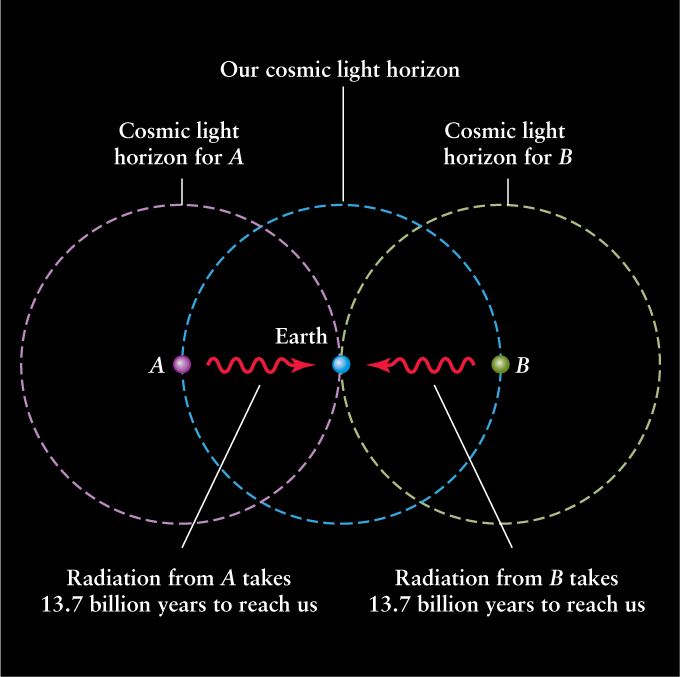
To appreciate why the uniformity of the microwave background poses a problem, think about two opposite parts of the sky, labeled A and B in Figure 26-1. Both of these points lie on a sphere centered on Earth; our observable universe lies within the sphere, and the surface is called our cosmic light horizon (see Section 25-3, especially Figure 25-5). We can see light coming from any object on or inside our cosmic light horizon, but we cannot yet see objects beyond this horizon. Even traveling at the speed of light—the ultimate speed limit—no information of any kind from objects beyond our cosmic light horizon has had time to reach us over the entire 13.7-billion-year history of the universe. Thus, the cosmic light horizon defines the limits of our observable universe. (As time passes, our cosmic light horizon expands, so eventually we will receive light from objects that are beyond the present-day horizon.)
Points A and B in Figure 26-1 lie near the distant edge of the observable universe, just inside our cosmic light horizon, so when we look at these points we are seeing about as far back into the past as possible—that is, the light we see from these points is the cosmic background radiation. In order for the radiation that reaches us from A and B to be nearly the same, the material of the early universe at A must have had the same temperature as at B. But for two objects to be at the same temperature, they should have been in contact and able to exchange heat with each other. (A hot cup of coffee and a cold spoonful of cream reach the same temperature only after you pour the cream into the coffee.)
The problem is that the widely separated regions at A and B have absolutely no connection with each other. As Figure 26-1 shows, point A lies outside the cosmic light horizon for point B, and point B lies outside the cosmic light horizon for point A. (Put another way, point A lies outside the observable universe of point B and vice versa.) Hence, no information has had time to travel between points A and B over the entire history of the universe. How is it possible, then, that these unrelated parts of the universe have almost exactly the same temperature? This dilemma is called the isotropy problem or the horizon problem. (Isotropy means uniformity in all directions.)
Even when we consider that the contents of the universe were closer together at earlier times in the universe, the isotropy problem does not go away. While it takes less time for closer regions to come into contact with each other, there is also less time for this to occur because the universe is not as old. When both of these effects are taken into account, there does not seem to be a way for the most distant regions to have reached the same temperature.
The Flatness Problem: Why Is Ω0 = 1?
The flatness of our universe presents us with a second enigma. Recall that the geometry of our universe depends on the density parameter Ω0, which is the ratio of the combined average mass density in the universe (ρ0) to the critical density (ρc) (this includes dark energy; see Section 25-6). Observations of temperature variations in the cosmic microwave background indicate that Ω0 is very close to 1, which corresponds to a flat universe.
For the density parameter Ω0 to be close to 1 today, it must have been extremely close to 1 during the Big Bang. In other words, the density of the early universe was almost exactly equal to the critical density. (The density was much higher than it is today, but the value of the critical density was also much higher. In a flat universe, the average mass density and the critical density decrease together as the universe expands, so that they remain equal at all times.)
The equations for an expanding universe show that any deviation from exact equality would have mushroomed within a fraction of a second. Had the average mass density been slightly less than ρc, the universe would have expanded so rapidly that matter could never have clumped together to form galaxies. Without galaxies, there would be no stars or planets, and humans would never have evolved. If, on the other hand, the density had been slightly greater than ρc, the universe would soon have become tightly packed with matter. Had this been the case, the gravitational attraction of this matter would long ago have collapsed the entire cosmos in a reversed Big Bang or “Big Crunch,” and again humans would never have evolved.
In other words, immediately after the Big Bang the fate of the universe hung in the balance. The tiniest deviation from the precise equality ρ0 = ρc would have rapidly propelled the universe away from the special case of Ω0 = 1. Had there been such a deviation, we would not be here to contemplate the nature of the universe.
Happily, our universe is one in which galaxies, stars, planets, and humans do exist, a Big Crunch has not taken place, and Ω0 is very close to 1. These conditions in the universe today tell us that the density of the universe immediately after the Big Bang must have been equal to the critical density to an incredibly high order of precision. In order for space to be as flat as it is today, the value of ρ0 right after the Big Bang must have been equal to ρc to more than 50 decimal places! Unless there was a physical mechanism to bring these two parameters into such close agreement, this extraordinary match is an unappealing characteristic for a scientific theory because it seems to depend on a lucky coincidence.
What could have happened during the first few moments of the universe to ensure that ρ0 = ρc to such an astounding degree of accuracy? Because ρ0 = ρc means that space is flat, this enigma is called the flatness problem.
Solving the Problems: The Inflationary Model
In the early 1980s, a remarkable solution was proposed to both the isotropy problem and the flatness problem. Several physicists suggested that the universe might have experienced a brief period of inflation, or extremely rapid expansion, shortly after the Planck time. (As we saw in Section 25-3, before the Planck time the normal laws of physics do not properly describe the behavior of space, time, and matter.) During this inflationary epoch, the universe expanded outward in all directions by a factor of about 1050. This epoch of dramatic expansion may have lasted only about 10−32 of a second (Figure 26-2).
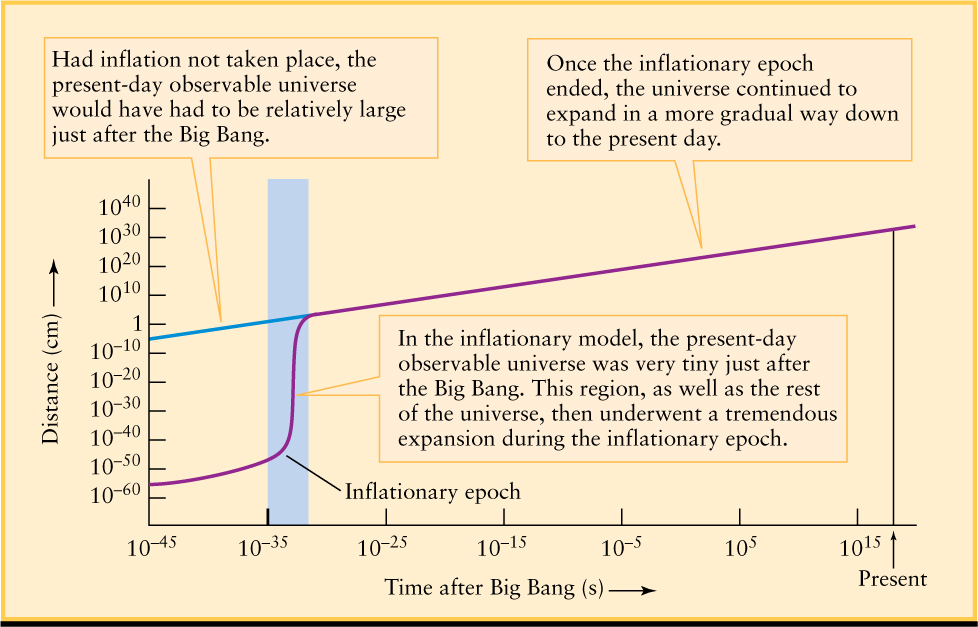
The inflationary model explains not only why the cosmic microwave background is so uniform, but also how stars, galaxies, and humans can exist
Inflation accounts for the isotropy of the microwave background. During the inflationary epoch, much of the material that was originally near our location was moved out to tremendous distances. Over the past 13.7 billion years, our cosmic light horizon has expanded so that we can see radiation from these distant regions. Hence, when we examine microwaves from opposite parts of the sky, we are seeing radiation from parts of the universe that were originally in intimate contact with one another. This contact allowed for the exchange of heat and is why all parts of the sky have almost exactly the same temperature.
ANALOGY
An inflationary epoch can also account for the flatness of the universe. To see why, think about a small portion of Earth’s spherical surface, such as a small lake. For all practical purposes, it is impossible to detect Earth’s curvature over such a small area, and a small lake looks flat. Similarly, the observable universe is such a tiny fraction of the entire inflated universe that any overall curvature in it is virtually undetectable (Figure 26-3). Like a small lake, the segment of space we can observe looks flat.
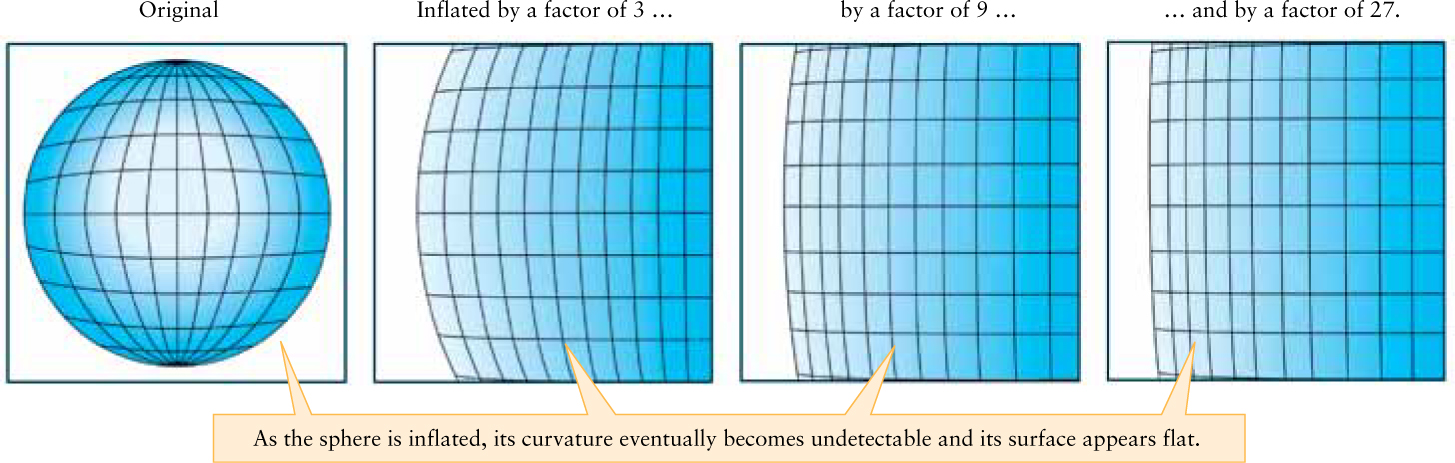
Not only does tremendous inflation produce a nearly flat universe, but it does so for just about any original degree of curvature prior to inflation. Let us consider why this is very appealing for a scientific theory. Recall that the flatness of our present universe could be explained (in an unsatisfactory way) if, by extraordinary coincidence alone, the value of ρ0 right after the Big Bang was equal to ρc for the first 50 decimal places. Also recall that curvature is determined by ρ0 (Section 25-6 and Table 25-1), where ρ0 = ρc is flat. Since Figure 26-3 shows that inflation flattens out just about any original degree of curvature, inflation also drives any initial value of ρ0 toward ρc, and removes the need for an unlikely coincidence alone to account for a flat universe.
CAUTION!
It is important to note that the concept of inflation does not violate Einstein’s law that nothing can travel faster than the speed of light. Remember that the expansion of the universe is the expansion of space itself, not the motion of objects through space. During the inflationary epoch, the distances between particles increased faster than the speed of light, but this was entirely the result of a sudden vigorous expansion of space. Particles did not move through space faster than the speed of light; space itself inflated to increase the distance between the particles. Even today, galaxies at redshifts greater than about z = 1.5 are receding faster than the speed of light.
Inflation and Polarization of the Cosmic Microwave Background
As we saw in Section 25-8, the detailed properties of temperature fluctuations in the cosmic microwave background, or CMB, can reveal a number of the fundamental parameters that describe our universe. This impressive list includes the Hubble constant, the density parameters for the total energy and for ordinary matter, and also for dark energy. In the near future, even the inflation model can be tested by measuring the polarization of light in the CMB.
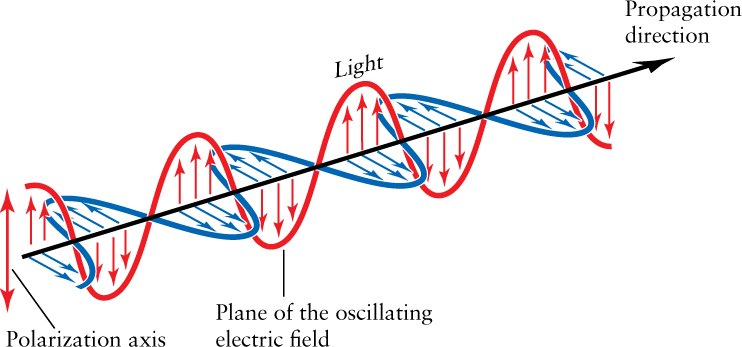
As illustrated in Figure 26-4, light can be polarized. Ordinary light from a lightbulb or from the Sun is unpolarized, which means that the electric fields of many light waves are oriented in random directions. But when light collides with and bounces off an object, it tends to become polarized, with its electric fields oriented in a specific direction. In a similar way, the cosmic background radiation acquires a polarization when it scatters from material in a dense cold spot (Figure 26-5).
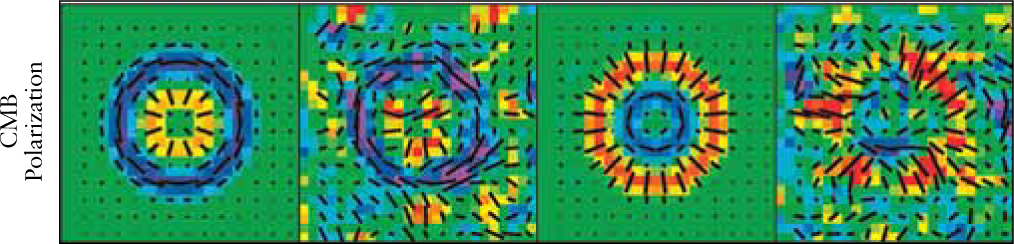
Polarization of the Cosmic Microwave Background The polarization axes of CMB light are indicated by the orientation of the small black lines. In the two spots on the left, as CMB radiation scatters off of denser regions in the early universe, a unique ring-structured polarization pattern is created. These are the regions that show up as cooler blue spots in images of the CMB temperature fluctuations (such as Figure 25-13). In the two spots on the right, a unique pattern is also created when the CMB scatters off of warmer regions of matter. While these polarization measurements agree with predictions, they are not sensitive enough to test the inflation model, and more sensitive experiments have already begun.
The effects of inflation are also expected to produce an additional and uniquely polarized CMB signature, although measurements from WMAP (Figure 26-5) were unable to detect these weak signals. However, there are several experiments that hope to detect CMB polarization produced by inflation (these include the Planck satellite, BICEP, and POLARBEAR). These are crucial experiments, as inflation is one of the most profound predictions about our early universe, and CMB polarization appears to be our best hope of testing the inflation model.
CONCEPT CHECK 26-1
In Figure 26-1, points A and B appear too far apart to reach the same temperature by exchanging energy with each other. Nonetheless, distant locations like this in the universe do show nearly the same 2.7 K temperatures. How does the inflation model solve this problem?
Early expansion is different in the inflation model compared to the gradual Hubble expansion. As shown in Figure 26-2, the inflationary model predicts an even smaller universe at early times than that described by gradual expansion. In this more compact condition, much more material would be in contact and reach the same temperature. Then, during inflation, this matter would get spread out so much that today this matter is at opposite ends of our observable universe (such as points A and B).
CONCEPT CHECK 26-2
Suppose the curvature of the universe before inflation was represented by the surface of a sphere that was 1 billion times smaller than the sphere on the left of Figure 26-3. With this high degree of initial curvature, could inflation have produced a universe that appears nearly flat today?
Yes. Inflation expands the universe by about a factor of 1050. With the curved space of the universe represented on the surface of a sphere, after the radius of the sphere increases during inflation by a factor of 1050, the surface (and universe) would appear flat. Due to tremendous inflation, just about any initial curvature ends up nearly flat after inflation.