4-2 Nicolaus Copernicus devised the first comprehensive heliocentric model

During the first half of the sixteenth century, a Polish lawyer, physician, canon of the church, and gifted mathematician named Nicolaus Copernicus (Figure 4-4) began to construct a new model of the universe. His model, which placed the Sun at the center, explained the motions of the planets in a more natural way than the Ptolemaic system. As we will see, it also helped lay the foundations of modern physical science. But Copernicus was not the first to conceive a Sun-centered model of planetary motion. In the third century b.c.e., the Greek astronomer Aristarchus suggested such a model as a way to explain retrograde motion.
A Heliocentric Model Explains Retrograde Motion
Imagine riding on a fast racehorse. As you pass a slowly walking pedestrian, he appears to move backward, even though he is traveling in the same direction as you and your horse. This sort of simple observation inspired Aristarchus to formulate a heliocentric (Sun-centered) model in which all the planets, including Earth, revolve about the Sun. Different planets take different lengths of time to complete an orbit, so from time to time one planet will overtake another, just as a fast-moving horse overtakes a person on foot. When Earth overtakes Mars, for example, Mars appears to move backward in retrograde motion, as Figure 4-5 shows. Thus, in the heliocentric picture, the occasional retrograde motion of a planet is merely the result of Earth’s fast motion.
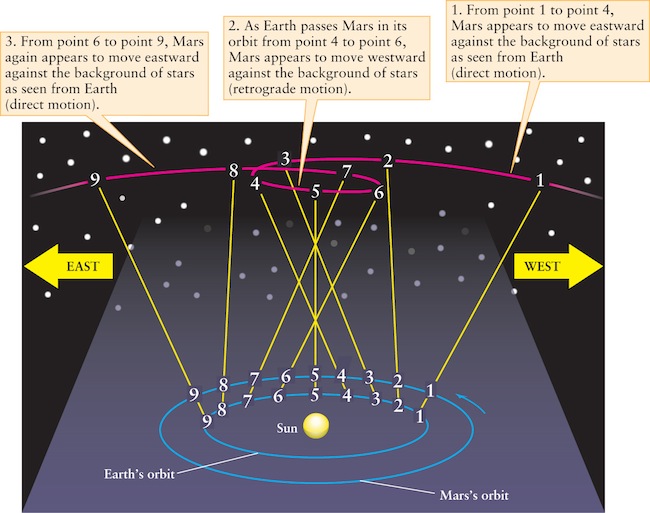
 A Heliocentric Explanation of Retrograde Motion In the heliocentric model of Aristarchus, Earth and the other planets orbit the Sun. Earth travels around the Sun more rapidly than Mars. Consequently, as Earth overtakes and passes this slower-moving planet, Mars appears for a few months (from points 4 through 6) to fall behind and move backward with respect to the background of stars.
A Heliocentric Explanation of Retrograde Motion In the heliocentric model of Aristarchus, Earth and the other planets orbit the Sun. Earth travels around the Sun more rapidly than Mars. Consequently, as Earth overtakes and passes this slower-moving planet, Mars appears for a few months (from points 4 through 6) to fall behind and move backward with respect to the background of stars.
The retrograde motion of the planets is a result of our viewing the universe from a moving Earth
As we saw in Section 3-6, Aristarchus demonstrated that the Sun is bigger than Earth (see Table 3-3). This made it sensible to imagine Earth orbiting the larger Sun. He also imagined that Earth rotated on its axis once a day, which explained the daily rising and setting of the Sun, Moon, and planets and the diurnal motions of the stars. To explain why the apparent motions of the planets never take them far from the ecliptic, Aristarchus proposed that the orbits of Earth and all the planets must lie in nearly the same plane. (Recall from Section 2-5 that the ecliptic is the projection onto the celestial sphere of the plane of Earth’s orbit.)
This heliocentric model is conceptually much simpler than an Earth-centered system, such as that of Ptolemy, with all its “circles upon circles.” In Aristarchus’s day, however, the idea of an orbiting, rotating Earth seemed inconceivable, given Earth’s apparent stillness and immobility. Nearly 2000 years would pass before a heliocentric model found broad acceptance.
CONCEPT CHECK 4-4
In the heliocentric model, could an imaginary observer on the Sun look out and see planets moving in retrograde motion?
No. A planet only appears to move in retrograde motion if seen from another planet if the two planets move at different speeds and pass one another (Figure 4-5). An imaginary observer on the stationary Sun would only see planets moving in the same direction as they orbit the Sun.
Copernicus and the Arrangement of the Planets
In the years after 1500, Copernicus came to realize that a heliocentric model has several advantages beyond providing a natural explanation of retrograde motion. In the Ptolemaic system, the arrangement of the planets—that is, which are close to Earth and which are far away—was chosen in large part by guesswork. By using a heliocentric model, Copernicus could determine the arrangement of the planets without ambiguity.
Copernicus realized that because Mercury and Venus are always observed fairly near the Sun in the sky, their orbits must be smaller than Earth’s. Planets in such orbits are called inferior planets (Figure 4-6). The other visible planets—Mars, Jupiter, and Saturn—are sometimes seen on the side of the celestial sphere opposite the Sun, so these planets appear high above the horizon at midnight (when the Sun is far below the horizon). When this happens, Earth must lie between the Sun and these planets. Copernicus therefore concluded that the orbits of Mars, Jupiter, and Saturn must be larger than Earth’s orbit. Hence, these planets are called superior planets.
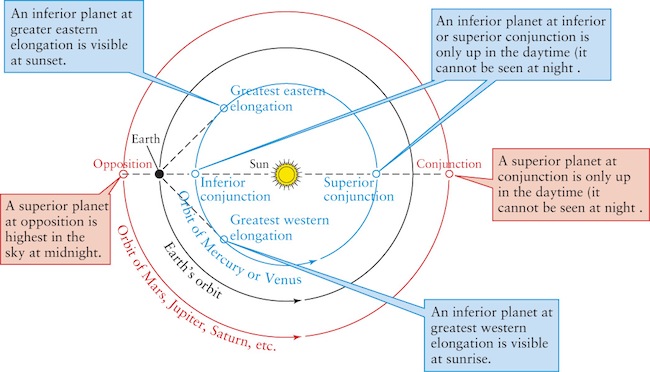
Uranus and Neptune, as well as Pluto and a number of other small bodies called asteroids that also orbit the Sun, were discovered after the telescope was invented (and after the death of Copernicus). All of these can be seen at times in the midnight sky, so these also have orbits larger than that of Earth.
The heliocentric model also explains why planets appear in different parts of the sky on different dates. Both inferior planets (Mercury and Venus) go through cycles: The planet is seen in the west after sunset for several weeks or months, then for several weeks or months in the east before sunrise, and then in the west after sunset again.
Figure 4-6 shows the reason for this cycle. When Mercury or Venus is visible after sunset, it is near greatest eastern elongation. (The angle between the Sun and a planet as viewed from Earth is called the planet’s elongation.) The planet’s position in the sky is as far east of the Sun as possible, so it appears above the western horizon after sunset (that is, to the east of the Sun) and is often called an “evening star.” At greatest western elongation, Mercury or Venus is as far west of the Sun as it can possibly be. It then rises before the Sun, gracing the predawn sky as a “morning star” in the east. When Mercury or Venus is at inferior conjunction, it is between us and the Sun, and it moves from the evening sky into the morning sky over weeks or months. At superior conjunction, when the planet is on the opposite side of the Sun, it moves back into the evening sky.
A superior planet such as Mars, whose orbit is larger than Earth’s, is best seen in the night sky when it is at opposition. At this point in its orbit the planet is in the part of the sky opposite the Sun and is highest in the sky at midnight. This is also when the planet appears brightest, because it is closest to us. But when a superior planet like Mars is located behind the Sun at conjunction, it is above the horizon during the daytime and thus is not well placed for nighttime viewing.
CONCEPT CHECK 4-5
How many times is Mars at inferior conjunction during one orbit around the Sun?
Mars has an orbit around the Sun that is larger than Earth’s orbit. As a result, Mars never moves to a position between Earth and the Sun, so Mars never is at inferior conjunction (Figure 4-6).
Planetary Periods and Orbit Sizes
The Ptolemaic system has no simple rules relating the motion of one planet to another. But Copernicus showed that there are such rules in a heliocentric model. In particular, he found a correspondence between the time a planet takes to complete one orbit—that is, its period—and the size of the orbit.
Determining the period of a planet takes some care, because Earth, from which we must make the observations, is also moving. Realizing this, Copernicus was careful to distinguish between two different periods of each planet. The synodic period is the time that elapses between two successive identical configurations as seen from Earth—from one opposition to the next, for example, or from one conjunction to the next. The sidereal period is the true orbital period of a planet, the time it takes the planet to complete one full orbit of the Sun relative to the stars.
The synodic period of a planet can be determined by observing the sky from Earth, but the sidereal period has to be found by calculation. Copernicus figured out how to do this (Box 4-1). Table 4-1 shows the results for all of the planets.
| Planet | Synodic period | Sidereal period |
|---|---|---|
| Mercury | 116 days | 88 days |
| Venus | 584 days | 225 days |
| Earth | — | 1.0 year |
| Mars | 780 days | 1.9 years |
| Jupiter | 399 days | 11.9 years |
| Saturn | 378 days | 29.5 years |
| Uranus | 370 days | 84.1 years |
| Neptune | 368 days | 164.9 years |
To find a relationship between the sidereal period of a planet and the size of its orbit, Copernicus still had to determine the relative distances of the planets from the Sun. He devised a straightforward geometric method of determining the relative distances of the planets from the Sun using trigonometry. His answers turned out to be remarkably close to the modern values, as shown in Table 4-2.
| Planet | Copernican value (AU*) | Modern value (AU) |
|---|---|---|
| Mercury | 0.38 | 0.39 |
| Venus | 0.72 | 0.72 |
| Earth | 1.00 | 1.00 |
| Mars | 1.52 | 1.52 |
| Jupiter | 5.22 | 5.20 |
| Saturn | 9.07 | 9.55 |
| Uranus | — | 19.19 |
| Neptune | — | 30.07 |
| *1 AU = 1 astronomical unit = average distance from Earth to the Sun. | ||
The distances in Table 4-2 are given in terms of the astronomical unit (AU), which is the average distance from Earth to the Sun (Section 1-7). The astronomical unit is 1 AU = 1.496 × 108 km (92.96 million miles). However, Copernicus did not know the precise value of this distance, so he could only determine the relative sizes of the orbits of the planets. (Using the astronomical unit, the average distance from the Sun to each of the planets in kilometers can be determined from Table 4-2. A table of these distances is given in Appendix 2.)
By comparing Table 4-1 and Table 4-2, you can see the unifying relationship between planetary orbits in the Copernican model: The farther a planet is from the Sun, the longer it takes to travel around its orbit (that is, the longer its sidereal period). That is so for two reasons: (1) the larger the orbit, the farther a planet must travel to complete an orbit; and (2) the larger the orbit, the slower a planet moves. For example, Mercury, with its small orbit, moves at an average speed of 47.9 km/s (107,000 mi/h). Saturn travels around its large orbit much more slowly, at an average speed of 9.64 km/s (21,600 mi/h). The older Ptolemaic model offers no such simple relations between the motions of different planets.
BOX 4-1 TOOLS OF THE ASTRONOMER’S TRADE
Relating Synodic and Sidereal Periods
We can derive a mathematical formula that relates a planet’s sidereal period (the time required for the planet to complete one orbit) to its synodic period (the time between two successive identical configurations). To start with, let us consider an inferior planet (Mercury or Venus) orbiting the Sun as shown in the accompanying figure. Let P be the planet’s sidereal period, S the planet’s synodic period, and E Earth’s sidereal period or sidereal year (see Section 2-8), which Copernicus knew to be nearly 365¼ days.
The rate at which Earth moves around its orbit is the number of degrees around the orbit divided by the time to complete the orbit, or 360°/E (equal to a little less than 1° per day). Similarly, the rate at which the inferior planet moves along its orbit is 360°/P.
During a given time interval, the angular distance that Earth moves around its orbit is its rate, (360°/E), multiplied by the length of the time interval. Thus, during a time S, or one synodic period of the inferior planet, Earth covers an angular distance of (360°/E)S around its orbit. In that same time, the inferior planet covers an angular distance of (360°/P)S. Note, however, that the inferior planet has gained one full lap on Earth, and hence has covered 360° more than Earth has (see the figure). Thus, (360°/P)S = (360°/E)S + 360°. Dividing each term of this equation by 360°S gives
For an inferior planet:

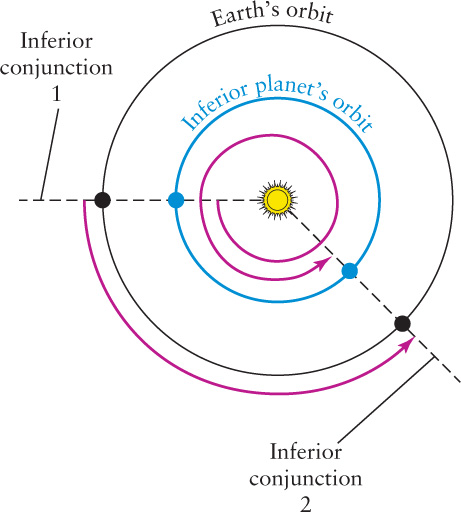
 A similar analysis for a superior planet (for example, Mars, Jupiter, or Saturn) yields
A similar analysis for a superior planet (for example, Mars, Jupiter, or Saturn) yields
For a superior planet:

Using these formulas, we can calculate a planet’s sidereal period P from its synodic period S. Often astronomers express P, E, and S in terms of years, by which they mean Earth years of approximately 365.26 days.
EXAMPLE: Jupiter has an observed synodic period of 398.9 days, or 1.092 years. What is its sidereal period?
Situation: Our goal is to find the sidereal period of Jupiter, a superior planet.
Tools: Since Jupiter is a superior planet, we use the second of the two equations given above to determine the sidereal period P.
Answer: We are given Earth’s sidereal period E = 1 year and Jupiter’s synodic period S = 1.092 years. Using the equation 1/P = 1/E − 1/S,
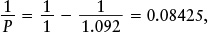
so
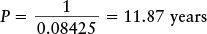
Review: Our answer means that it takes 11.87 years for Jupiter to complete one full orbit of the Sun. This sidereal period is greater than Earth’s 1-year sidereal period because Jupiter’s orbit is larger than Earth’s orbit. Jupiter’s synodic period of 1.092 years is the time from one opposition to the next, or the time that elapses from when Earth overtakes Jupiter to when it next overtakes Jupiter. This synodic period is so much shorter than the sidereal period because Jupiter moves quite slowly around its orbit. Earth overtakes it a little less often than once per Earth orbit, that is, at intervals of a little bit more than a year.
CONCEPT CHECK 4-6
What causes the planets to stop and change their direction of motion through the sky in the heliocentric model?
In Copernicus’s heliocentric model, the more distant planets are moving slower than the planets closer to the Sun. As a faster-moving Earth moves past a slower-moving Mars, there is a brief time in which Mars appears to move backward through the sky. However, the planets never actually reverse their directions.
CONCEPT CHECK 4-7
Why is Jupiter’s sidereal period longer than its synodic period?
Slowly moving Jupiter does not move very far along its orbit in the length of time it takes for Earth to pass by Jupiter, move around the Sun, and pass by Jupiter again, giving Jupiter a synodic period similar to Earth’s orbital period around the Sun. However, slow-moving Jupiter takes more than a decade to move around the Sun back to its original starting place as measured by the background stars, giving it a large sidereal period.
The Shapes of Orbits in the Copernican Model
At first, Copernicus assumed that Earth travels around the Sun along a circular path. He found, however, that perfectly circular orbits could not accurately describe the paths of the other planets, so he had to add an epicycle to each planet. These epicycles were not added to explain retrograde motion, which Copernicus realized was because of the differences in orbital speeds of different planets, as shown in Figure 4-5. Rather, the small epicycles helped Copernicus account for slight variations in each planet’s speed along its orbit.
Even though he clung to the old notion that orbits must be made up of circles, Copernicus had shown that a heliocentric model could explain the motions of the planets. He compiled his ideas and calculations into a book entitled De revolutionibus orbium coelestium (On the Revolutions of the Celestial Spheres), which was published in 1543, the year of his death.
For several decades after Copernicus, most astronomers saw little reason to change their allegiance from the older geocentric model of Ptolemy. The predictions that the Copernican model makes for the apparent positions of the planets are, on average, no better or worse than those of the Ptolemaic model. The test of Occam’s razor does not really favor either model, because both use a combination of circles to describe each planet’s motion.
More concrete evidence was needed to convince scholars to abandon the old, comfortable idea of a stationary Earth at the center of the universe. The story of how this evidence was accumulated begins nearly 30 years after the death of Copernicus, when a young Danish astronomer pondered the nature of a new star in the heavens.
CONCEPT CHECK 4-8
Why was Copernicus’s model more accurate than Ptolemy’s model?
Initially, Copernicus’s model was no more accurate at predicting the positions and motions of the planets than Ptolemy’s model. However, Copernicus’s model turned out to be more closely related to the actual motions of the planets around the Sun than was Ptolemy’s model of planets orbiting Earth. With subsequent measurements, Ptolemy’s model was proven wrong.