Using Properties of Double Integrals

Find \(\displaystyle\iint\limits_{\kern-3ptR} x^{2}y\,dA,\) where \(R\) is the region enclosed by the lines \(y=x,\) \(y=x+2\), \(y=-x+2,\) and \(y=-x+4.\)

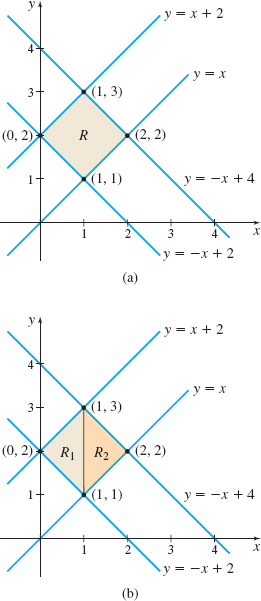
Solution We begin by graphing the region \(R\) as shown in Figure 19(a). We observe that \(R\) is a closed, bounded region, but it is neither \(x\) -simple nor \(y\)-simple. It is not \(x\)-simple due to the corners at \(( 1,3) \) and \((1,1) .\) It is not \(y\)-simple due to the corners at \(( 0,2) \) and \((2,2) .\) But we can partition \(R\) into subregions \(R_{1}\) and \(R_{2}\), both of which are \(x\)-simple, by drawing a vertical line from \(( 1,3) \) to \(( 1,1) \). See Figure 19(b). The subregion \(R_{1}\) is \(x\)-simple with \( g_{1}(x) =-x+2\); \(g_{2}(x)=x+2\), \(0\leq x\leq 1.\) The subregion \(R_{2}\) is \(x\)-simple with \(h_{1}(x) =x\); \( h_{2}(x)=-x+4\), \(1\leq x\leq 2.\) Then \begin{eqnarray*} \displaystyle\iint\limits_{\kern-3ptR}x^{2}y\,{\it dA} &=&\displaystyle\iint\limits_{\kern-3ptR_{1}}x^{2}y\,{\it dA}+\displaystyle\iint\limits_{\kern-3ptR_{2}}x^{2}y\,{\it dA}\\[4pt] &=&\int_{0}^{1} \left[ \int_{-x+2}^{x+2}x^{2}y\,{\it dy}\right] \! {\it dx}+\int_{1}^{2} \left[ \int_{x}^{-x+4}x^{2}y\,{\it dy}\right] \! {\it dx} \notag \\[4pt] &=&\int_{0}^{1} x^{2}\left[\dfrac{y^{2}}{2}\right] _{-x+2}^{x+2}\,{\it dx}+ \int_{1}^{2} x^{2}\left[\dfrac{y^{2}}{2}\right] _{x}^{-x+4}\,{\it dx} \notag \\[4pt] &=&\dfrac{1}{2}\int_{0}^{1}x^{2}\left[ (x+2) ^{2}-\left( -x+2\right) ^{2}\right] \! {\it dx}+\dfrac{1}{2}\int_{1}^{2}x^{2}\left[ \left( -x+4\right) ^{2}-x^{2}\right] \! {\it dx} \notag \\[4pt] &=&\dfrac{1}{2}\int_{0}^{1}8x^{3}\,{\it dx}+\dfrac{1}{2}\int_{1}^{2}(-8x^{3}+16x^{2}) \,{\it dx} \notag \\[4pt] &=&4\left[\dfrac{x^4}{4}\right]^1_0 - 4\left[\dfrac{x^4}{4}\right]^2_1 + 8 \left[\dfrac{x^3}{3}\right]^2_1 = 1-15+\dfrac{56}{3}=\dfrac{14}{3} \end{eqnarray*}