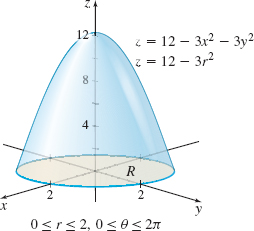
Finding the Volume of a Solid

Find the volume \(V\) of the solid under the circular paraboloid \( z=12-3x^{2}-3y^{2}\) and above the \(xy\)-plane.

Solution We begin by graphing the paraboloid for \(z\geq 0,\) as shown in Figure 29.

The region \(R\) is determined by the intersection of the surface \(z\) and the \( xy\)-plane. So, we let \(z=0\) and simplify the equation. \begin{eqnarray*} 12-3x^{2}-3y^{2} &=&0 \\[3pt] 3x^{2}+3y^{2} &=&12 \\[3pt] x^{2}+y^{2} &=&4 \end{eqnarray*}

So \(R\) is the region enclosed by the circle \(x^{2}+y^{2}=4\).

To convert the problem to polar coordinates, we let \(x=r\cos \theta\) and \( y=r\sin \theta.\) Then the paraboloid is \(z=12-3x^{2}-3y^{2}=12-3(x^{2}+y^{2}) =12-3r^{2},\) and the region \(R\) is enclosed by the circle \(r^{2}=4.\) So, \(R\) is given by \(0\leq r\leq 2\) and \(0\leq \theta \leq 2\pi.\)

Then \[ \begin{eqnarray*} V &=&\displaystyle\iint\limits_{\kern-3ptR}( 12-3x^{2}-3y^{2})\, {\it dA}\underset{\underset{\color{#0066A7}{\hbox{$\begin{array}{c}3x^{2}+3y^{2}=3r^{2}\\ {dA}=r\,{dr}\,d\theta\end{array}$}}} {\color{#0066A7}{\uparrow}}}{=} \int\nolimits_{0}^{2\pi }\!\!\!\int_{0}^{2}( 12-3r^{2})\, r\,{\it dr}\,d\theta = \int_{0}^{2\pi }\!\!\!\int_{0}^{2}( 12r-3r^{3})\, dr\, d\theta \\[-15.5pt] &=&\int_{0}^{2\pi }\left[ 6r^{2}-3\dfrac{r^{4}}{4}\right] _{0}^{2}~d\theta = \int_{0}^{2\pi }12~d\theta =\big[ 12\theta \big] _{0}^{2\pi }=24\pi \hbox{ cubic units} \end{eqnarray*} \]