Determining Whether a Piecewise-Defined Function Is Continuous

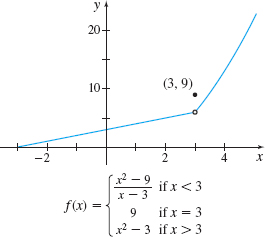
Determine if the function \begin{equation*} f(x)=\left\{ \begin{array}{c@{\qquad}l} \dfrac{x^{2}-9}{x-3} & \hbox{if }x\lt 3 \\ 9 & \hbox{if }x=3 \\[5pt] x^{2}-3 & \hbox{if }x>3 \end{array} \right. \end{equation*}

is continuous at \(3\).

95

Solution Since \(f(3)=9\), the function \(f\) is defined at \(3\). To check the second condition, we investigate the one-sided limits. \[ \begin{eqnarray*} \lim_{x\rightarrow 3^{-}}f(x) &=&\lim_{x\rightarrow 3^{-}}\frac{x^{2}-9}{x-3 }=\lim_{x\rightarrow 3^{-}}\frac{( x-3) ( x+3) }{x-3} \underset{\underset{\color{#0066A7}{\hbox{Divide out \(x-3\)}}}{\color{#0066A7}{\uparrow}}} {=}\lim_{x\rightarrow 3^{-}}(x+3)=6 \\ \lim_{x\rightarrow 3^{+}}f(x) &=&\lim_{x\rightarrow 3^{+}} (x^{2}-3) =9-3=6 \end{eqnarray*} \]

Since \(\lim\limits_{x\rightarrow 3^{-}}f(x)=\lim\limits_{x\rightarrow 3^{+}}f(x)\), then \(\lim\limits_{x\rightarrow 3}f(x)\) exists. But, \(\lim\limits_{x\rightarrow 3}f(x)=6\) and \(f(3)=9\), so the third condition of continuity is not satisfied. The function \(f\) is discontinuous at \(3\).

Figure 24 shows the graph of \(f\).