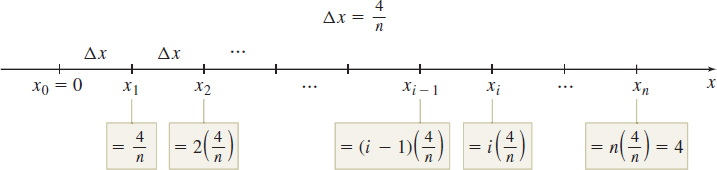Finding Area Using Lower Sums

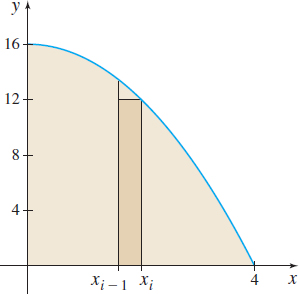
Find the area \(A\) under the graph of \(f(x) = 16 - x^{2}\) from \(0\) to \(4\) by using lower sums \(s_{n}\) (rectangles that lie below the graph of \(f\)). Then \(A=\lim\limits_{n\rightarrow \infty }{}s_{n}\).

Solution Figure 14 shows the area under the graph of \(f\) and a typical rectangle that lies below the graph. We partition the closed interval \([0,4]\) into \(n\) subintervals \[ {[{x_{0},x_{1}}]}, {[{x_{1},x_{2}}]}, \ldots , [x_{i-1},x_{i}], \ldots , {[{x_{n-1},x_{n}}]} \]

where \[ 0=x_{0}\lt x_{1}\lt\cdots \lt x_{i}\lt\cdots \lt x_{n-1}\lt x_{n}=4 \]

and each interval is of length \[ \Delta x = \dfrac{{4-0}}{n} = \dfrac{4}{n} \]

As Figure 15 on page 350 illustrates, the endpoints of each subinterval, written in terms of \(n\), are \[ \begin{eqnarray*} x_{0} &=& 0,\ x_{1}=1\left( \dfrac{4}{n}\right)\!,\ x_{2}=2\left( {{\dfrac{{4}}{{n}}}}\right), \ldots , x_{i-1}=(i-1) \left( {{\dfrac{{4}}{{n}}}}\right), \\ x_{i} &=& i\left( {{\dfrac{{4}}{{n}}}} \right)\!, \ldots , x_{n}=n\left( {{\dfrac{{4}}{{n}}}}\right) =4 \end{eqnarray*} \]

350

To find \(A\) using lower sums \(s_{n}\) (rectangles that lie below the graph of \(f\)), we must find the absolute minimum value of \(f\) on each subinterval. Since the function \(f\) is a decreasing function, the absolute minimum occurs at the right endpoint of each subinterval. So, \[ s_{n}={\sum\limits_{i=1}^{n}} f (c_{i})\Delta x \]

Since \(c_{i}=i \left( \dfrac{4}{n}\right) =\dfrac{4i}{n}\) and \(\Delta x=\dfrac{4}{n}\), we have

\[ \begin{eqnarray*} s_{n} &=&\sum\limits_{i=1}^{n}f(c_{i})\Delta x = \sum \limits_{i=1}^{n}\left[ {16-{{\left( {{\dfrac{{4i}}{{n}}}}\right) }}^{2}} \right] \left( {{\dfrac{{4}}{{n}}}}\right) {\color{#0066A7}{(c_i = \dfrac{4i}{n}); f(c_{i}) = 16 - c_{i}^{2}}}\\ &=& \sum\limits_{i=1}^{n}\left[ \dfrac{64}{n}-\dfrac{64i^{2}}{n^{3}}\right] \\ &=& \dfrac{64}{n}{{{\sum\limits_{i=1}^{n}1}}}-\dfrac{64}{n^{3}}\sum\limits_{i=1}^{n}i^{2} \\ &=& \dfrac{64}{n}(n) -\dfrac{64}{n^{3}}\left[ \dfrac{n(n+1) (2n+1) }{6}\right] = 64-\dfrac{32}{3n^{2}}\left[ 2n^{2}+3n+1\right] \\ &=& 64-\dfrac{64}{3}-\dfrac{32}{n}-\dfrac{32}{3n^{2}}=\dfrac{128}{3}-\dfrac{32}{n}-\dfrac{32}{3n^{2}} \end{eqnarray*} \]

Then \[ A=\lim\limits_{n\rightarrow \infty }s_{n}={\lim\limits_{n\rightarrow \infty }}\left( {{\dfrac{{128}}{{3}}}}-{{\dfrac{{32}}{{n}}}-{\dfrac{{32}}{{3n^{2}}}}}\right) ={\dfrac{{128}}{{3}}} \]

The area \(A\) under the graph of \(f (x) =16-x^{2}\) from \(0\) to \(4\) is \(\dfrac{128}{3}\) square units.