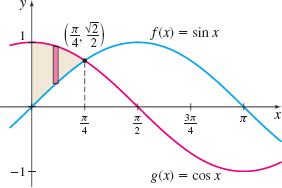
Finding the Area Between the Graphs of Two Functions

Find the area of the region enclosed by the graphs of \(f(x)=\sin x\) and \(g(x)=\cos x\) from the \(y\)-axis to their first point of intersection in the first quadrant.

Solution First we graph the two functions. See Figure 5.

The points of intersection of the two graphs satisfy the equation \(f(x)= g(x)\). \[ \begin{array}{rcl@{\qquad}l} \sin x &=&\cos x & \qquad {\color{#0066A7}{f (x) =g ( x )}} \\[4pt] \tan x &=&1 \end{array} \]

The first point of intersection in the first quadrant occurs at \(x=\tan ^{-1}1=\dfrac{\pi}{4}.\) The graphs intersect at the point \(\left( \dfrac{\pi}{4},\,\dfrac{\sqrt{2}}{2}\right)\), so the area \(A\) we seek lies between \(x=0\) and \(x=\dfrac{\pi}{4}.\) Since \(\cos x\geq \sin x\) on \(\left[ 0,\dfrac{\pi}{4}\right]\), the area \(A\) is given by \begin{eqnarray*} A&=&\int_{0}^{\pi /4}\left( \cos x-\sin x\right) ~{\it dx}=~\big[ \sin x+\cos x \hbox{ }\big] _{0}^{\pi /4}=\left( \frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} \right) -(0+1)\\[5pt] &=&\sqrt{2}-1 \hbox{ square units} \end{eqnarray*}