EXAMPLE 2Approximating \(y=\sqrt{1+x}\)
- (a) Write the Maclaurin expansion for \(y=\sqrt{1+x}\) using a binomial series.
- (b) Approximate \(\sqrt{1+x}\) using the first five terms of the Maclaurin series.
- (c) Graph \(y=\sqrt{1+x}\) together with the first five terms of the approximation found in (b).
- (d) Comment on the graphs in (c).
- (e) Use the first five terms of the approximation for \(\sqrt{1+x}\) to approximate \(\sqrt{1.2}\). What is the error in using this approximation.
Solution (a) For \(-1\leq x\leq 1\), we have \begin{eqnarray}\quad \sqrt{1+x} &=&(1+x) ^{1/2}=\sum\limits_{k\,=\,0}^{\infty }{{ \dfrac{1}{2}}\choose {\vphantom{\vrule height10pt depth.2pt}k}}\,x^{k} \nonumber\\[8pt] &=& {1}+\dfrac{1}{2}{\,}x+\dfrac{\dfrac{1}{2}\left( - \dfrac{1}{2}\right) }{2!}x^{2}+\dfrac{\dfrac{1}{2}\,\left( -\dfrac{1}{2} \right) \left( -\dfrac{3}{2}\right) }{3!}\,x^{3}+\cdots +{{\dfrac{1}{2 }}\choose {\vphantom{\vrule height10pt depth.2pt}n}}x^{n}+\cdots \nonumber \end{eqnarray}
625
(b) From part (a), we have \[ \begin{equation*} \sqrt{1+x} \approx 1+\dfrac{1}{2}x-\dfrac{1}{8}x^{2}+\dfrac{1}{16}x^{3}-\dfrac{5}{128}x^{4} \tag{2} \end{equation*} \]
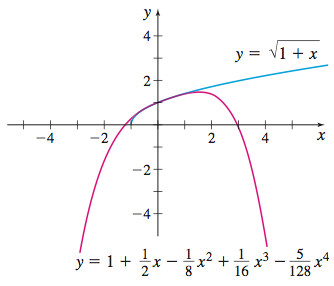
(c) The graphs of \(y=\sqrt{1+x}\) and the first five terms of the approximation in (2) are given in Figure 30.
(d) On the interval of convergence \([-1,1]\), the graphs are almost identical. Outside this interval, the graphs diverge.
(e) Using (2) and \(x=0.2,\) we have \[ \sqrt{1.2}\approx 1+\dfrac{1}{2}(0.2) -\dfrac{1}{8}(0.2) ^{2}+\dfrac{1}{16}(0.2) ^{3}-\dfrac{5}{128}(0.2) ^{4}=1.0954375 \]
Since the binomial series for \(y=\sqrt{1+x}\) at \(x=0.2\) is an alternating series that satisfies the conditions of the Alternating Series Test, the error \(E\) in using the first five terms of the series as an approximation of \(\sqrt{1.2}\) is less than or equal to the absolute value of the 6th term at \(x=0.2.\) That is, \[ \begin{eqnarray*} &&E\leq \left\vert \dfrac{\dfrac{1}{2}\,\left( -\dfrac{1}{2}\right) \left( -\dfrac{3}{2}\right) \left( -\dfrac{5}{2}\right) \left(- \dfrac{7}{2}\right)}{5!}\,x^{5}\right\vert \underset{\underset{\color{#0066A7}{\scriptsize\hbox{x=0.2}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{7}{256}(0.2) ^{5}= 8.\, 75\times 10^{-6}\\[-23pt] \end{eqnarray*} \]