Graphing a Polar Equation (Limaçon with an Inner Loop); Finding Parametric Equations

(a) Graph the polar equation \(r=1+2 \ \cos \theta,\;0\leq \theta\leq 2\pi.\)

(b) Find parametric equations for \(r=1+2 \ \cos \theta \).

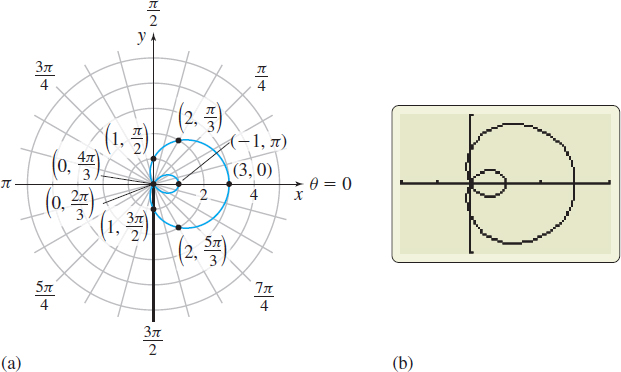
Solution (a) The polar equation \(r=1+2 \ \cos \theta\) contains \(\cos \theta\), which has the period \(2\pi .\) We construct Table 4 using common values of \(\theta \) that range from \(0\) to \(2\pi ,\) plot the points \(( r,\theta )\), and trace out the graph, beginning at the point \(\left(3,0\right)\) and ending at the point \(( 3, \ 2\pi )\), as shown in Figure 45(a). Figure 45(b) shows the graph using technology.

TABLE 4
\(\theta\) \(r=1+2 \ \cos \theta\) \(( r,\theta )\)
\(0\) \(1+2(1) =3\) \(( 3,0)\)
\(\dfrac{\pi }{3}\) \(1+2\left( \dfrac{1}{2}\right) =2\) \(\left( 2,\dfrac{\pi }{3}\right)\)
\(\dfrac{\pi }{2}\) \(1+2\left( 0\right) =1\) \(\left( 1,\dfrac{\pi }{2}\right)\)
\(\dfrac{2\pi }{3}\) \(1+2\left( -\dfrac{1}{2}\right) =0\) \(\left( 0,\dfrac{2\pi }{3}\right)\)
\(\pi\) \(1+2( -1) =-1\) \(\left( -1, \ \pi \right)\)
\(\dfrac{4\pi }{3}\) \(1+2\left( -\dfrac{1}{2}\right) =0\) \(\left( 0,\dfrac{4\pi }{3}\right)\)
\(\dfrac{3\pi }{2}\) \(1+2\left( 0\right) =1\) \(\left( 1,\dfrac{3\pi }{2}\right)\)
\(\dfrac{5\pi }{3}\) \(1+2\left( \dfrac{1}{2}\right) =2\) \(\left( 2,\dfrac{5\pi }{3}\right)\)
\(2\pi\) \(1+2( 1) =3\) \(( 3, \ 2\pi )\)
Figure 45 The limaçon \(r=1+2 \ \cos \theta\).

673

Graphs of polar equations of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{rcl@{\qquad}crcl} r&=&a+b \ \cos \theta & r=a+b \ \sin \theta\\ r&=&a-b \ \cos \theta & r=a-b \ \sin \theta \end{array} }} \]

where \(0\lt a\lt b,\) are called limaçons with an inner loop. A limaçon with an inner loop passes through the pole twice.

(b) We obtain parametric equations for \(r=1+2 \ \cos \theta\) by using the conversion formulas \(x=r \ \cos \theta\) and \(y=r \ \sin \theta\): \[ x=r \ \cos \theta =( 1+2 \ \cos \theta ) \ \cos \theta \qquad y=r \ \sin \theta =( 1+2 \ \cos \theta ) \ \sin \theta \]

Here, \(\theta\) is the parameter, and if \(0\leq \theta \leq 2\pi ,\) then the graph is traced out exactly once in the counterclockwise direction.