A.1 Algebra Used in CalculusPrinted Page A-1
1 Factor and Simplify Algebraic ExpressionsPrinted Page A-1
EXAMPLE 1Factoring Algebraic Expressions
Factor each expression completely:
(a) \(2( x+3) ( x-2) ^{3}+( x+3) ^{2}( 3) ( x-2) ^{2}\)
(b) \(\dfrac{4}{3}x^{1/3}( 2x+1) +2x^{4/3}\)
Solution (a) In expression (a), \(( x+3)\) and \(( x-2) ^{2}\) are common factors, factors found in each term. Factor them out. \[ \begin{array}{rcl@{\qquad\hspace*{-3pt}}l} &&2 ( x+3) ( x-2) ^{3}+ ( x+3) ^{2} ( 3) ( x-2) ^{2}\\[5pt] &&\quad = ( x+3) (x-2) ^{2} [ 2 ( x-2) +3 ( x+3) ] & {\color{#0066A7}{\hbox{Factor out \(\hbox{(}x+3\hbox{)}\,\hbox{(}x-2\hbox{)}^2\).}}} \\[5pt] &&\quad = ( x+3) ( x-2) ^{2} ( 5x+5) & {\color{#0066A7}{\hbox{Simplify.}}}\\[5pt] &&\quad = 5 ( x+3) ( x-2) ^{2} (x+1) & {\color{#0066A7}{\hbox{Factor out 5.}}} \end{array} \]
(b) We begin by writing the term \(2x^{4/3}\) as a fraction with a denominator of \(3\). \[ \begin{array}{rcl@{\qquad\hspace*{-5.5pt}}l} \dfrac{4}{3}x^{1/3} ( 2x+1) +2x^{4/3} &=&\dfrac{4x^{1/3} (2x+1) }{3}+\dfrac{6x^{4/3}}{3}\\[9pt] &=&\dfrac{4x^{1/3} ( 2x+1) +6x^{4/3}}{3} &{\color{#0066A7}{\hbox{Add the two fractions.}}}\\[9pt] &=&\dfrac{2x^{1/3} [ 2 ( 2x+1) +3x] }{3} &{\color{#0066A7}{\hbox{2 and \(x^{1/3}\) are common factors.}}}\\[9pt] &=&\dfrac{2x^{1/3} (7x+2) }{3} & {\color{#0066A7}{\hbox{Simplify.}}} \end{array} \]
A-2
EXAMPLE 2Simplifying Algebraic Expressions
(a) Simplify \(\dfrac{( x^{2}+1) ( 3) -( 3x+4) ( 2x) }{( x^{2}+1) ^{2}}\).
(b) Write the expression \(( x^{2}+1) ^{1/2}+x\cdot \dfrac{1}{2}( x^{2}+1) ^{-1/2}\cdot 2x\) as a single quotient in which only positive exponents appear.
Solution (a) \begin{eqnarray*} \ \dfrac{( x^{2}+1) (3) -( 3x+4) ( 2x) }{( x^{2}+1) ^{2}}&=&\dfrac{ 3x^{2}+3- ( 6x^{2}+8x) }{( x^{2}+1) ^{2}}=\dfrac{ 3x^{2}+3-6x^{2}-8x}{( x^{2}+1) ^{2}}\\[6pt] &=&\dfrac{-3x^{2}-8x+3}{( x^{2}+1) ^{2}}\underset{\underset{\color{#0066A7}{\hbox{Factor}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{- ( 3x-1) ( x+3) }{( x^{2}+1) ^{2}}\\ \end{eqnarray*}
(b) \begin{eqnarray*} ( x^{2}+1) ^{1/2}+x\cdot \dfrac{1}{2}( x^{2}+1) ^{-1/2}\cdot 2x&=&( x^{2}+1) ^{1/2}+\dfrac{x^{2}}{ ( x^{2}+1) ^{1/2}}\\[6pt] &=&\dfrac{( x^{2}+1) ^{1/2}( x^{2}+1) ^{1/2}}{( x^{2}+1) ^{1/2}}+\dfrac{x^{2}}{( x^{2}+1) ^{1/2}}\\[6pt] &=&\dfrac{( x^{2}+1) +x^{2}}{( x^{2}+1) ^{1/2}}=\dfrac{ 2x^{2}+1}{( x^{2}+1) ^{1/2}} \end{eqnarray*}
2 Complete the SquarePrinted Page A-2
We complete the square in one variable by modifying an expression of the form \(x^{2}+bx\) to make it a perfect square. Perfect squares are trinomials of the form \[ x^{2}+2ax+a^{2}= ( x+a) ^{2}\hbox{ or } x^{2}-2ax+a^{2}= ( x-a) ^{2}\hbox{ } \]
For example, \(x^{2}+6x+9\) \(\ \)is a perfect square because \(x^{2}+6x\,{+}\,9=( x+3) ^{2}\). And \(p^{2}-12p+36\) is a perfect square because \( p^{2}-12p+36= ( p-6) ^{2}.\)
To make \(x^{2}+6x\) a perfect square, we must add \(9.\) The number to be added is chosen by dividing the coefficient of the first-degree term, which is \(6,\) by \(2\) and squaring the result \(\left[ \left( \dfrac{6}{2}\right) ^{\!\!2}\!=9 \right] \).
EXAMPLE 3Completing the Square
Determine the number that must be added to each expression to complete the square. Then factor.
| Start | Add | Result | Factored Form |
|---|---|---|---|
| \(y^{2}+8y\) | \(\left( \dfrac{1}{2}\cdot 8\right) ^{\!\!2}=16\) | \(y^{2}+8y+16\) | \(( y+4) ^{2}\) |
| \(a^{2}-20a\) | \(\left( \dfrac{1}{2}\cdot ( -20) \right) ^{\!\!2}=100\) | \(a^{2}-20a+100\) | \( ( a-10) ^{2}\) |
| \(p^{2}-5p\) | \(\left( \dfrac{1}{2}\cdot ( -5) \right) ^{\!\!2}= \dfrac{25}{4}\) | \(p^{2}-5p+\dfrac{25}{4}\) | \(\left( p-\dfrac{5}{2} \right) ^{\!\!2}\) |
| \(2x^{2}+6x=2 ( x^{2}+3x)\) | \(\left( \dfrac{1}{2}\cdot 3\right) ^{\!\!2}=\dfrac{9}{4}\) | \(2\!\left( x^{2}+3x+\dfrac{9}{4}\right)\) | \(2\!\left( x+\dfrac{3}{2}\right) ^{\!\!2}\) |
A-3
CAUTION The original expression \(x^{2}+bx\) and the perfect square \( x^{2}+bx+\left( \dfrac{b}{2}\right) ^{\!\!2}\) are not equal. So when completing the square within an equation or an inequality, we must not only add \( \left( \dfrac{b}{2}\right) ^{\!\!2}\!\), we must also subtract it. That is, \[ x^{\!\!2}+bx=x^{\!\!2}+bx+{\hbox{\(\stackrel{\underbrace{\left(\dfrac{b}{2}\right) ^{\!\!2}-\left( \dfrac{b}{2}\right) ^{\!\!2}}}{=0}\)}}=\left( x+\dfrac{b}{2}\right) ^{\!\!2}-\left( \dfrac{b}{2}\right) ^{\!\!2} \]
3 Solve EquationsPrinted Page A-3
To solve a quadratic equation \(ax^{2}+bx+c=0,\) \(a\neq 0\), the quadratic formula can be used.
THEOREM Quadratic Formula
Consider the quadratic equation \[ ax^{2}+bx+c=0\hbox{ } \quad a\neq 0 \]
If \(b^{2}-4ac<0\), the equation has no real solution.
If \(b^{2}-4ac\geq 0\), the real solution(s) of the equation is (are) given by the quadratic formula: \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a} } }\]
The expression \(b^{2}-4ac\) is called the discriminant of the quadratic equation.
EXAMPLE 4Solving Quadratic Equations
Solve the equations:
(a) \(3x^{2}-5x+1=0\)
(b) \(x^{2}+x=-1\)
Solution (a) The discriminant: \(b^{2}-4ac=25-12=13\). We use the quadratic formula. \[ x=\dfrac{-b\pm \displaystyle\sqrt{b^{2}-4ac}}{2a}=\dfrac{5\pm \displaystyle\sqrt{13}}{6} \]
The solutions are \(x=\dfrac{5-\sqrt{13}}{6}\approx 0.232\) and \(x=\dfrac{5+ \sqrt{13}}{6}\approx 1.434\)
(b) The equation in standard form is \(x^2+x+1=0\). Its discriminant is \(b^{2}-4ac=1-4=-3\). This equation has no real solution.
NOTE
Remember to put a quadratic equation in standard form before attempting to solve it. That is, write the quadratic equation in the form \(ax^{2}+bx+c=0.\)
EXAMPLE 5Solving Equations
Solve the equations:
(a) \(\dfrac{3}{x-2}=\dfrac{1}{x-1}+\dfrac{7}{( x-1) ( x-2) }\)
(b) \(x^{3}-x^{2}-4x+4=0\)
(c) \(\sqrt{x-1}=x-7\)
(d) \(\vert 1-x\vert =2\)
A-4
NOTE
The set of real numbers that a variable can assume is called the domain of the variable.
Solution (a) First, notice that the domain of the variable is \( \{ x~|~x\neq 1,\,x\neq 2\} \). Now clear the equation of rational expressions by multiplying both sides by \(( x-1) ( x-2) \). \[ \begin{array}{@{\hspace*{-7.1pc}}rcl@{\qquad}ll} \dfrac{3}{x-2}&=&\dfrac{1}{x-1}+\dfrac{7}{( x-1) ( x-2) }& \\ ( x-1) ( x-2) \dfrac{3}{x-2} &=&( x-1) ( x-2) \left[ \dfrac{1}{x-1}+\dfrac{7}{( x-1) ( x-2) }\right] & {\color{#0066A7}{\hbox{Multiply both sides by} }}\\ &&&{\color{#0066A7}{\hbox{\(( {x-1}) ( { x-2}).\)}}} \\ 3x-3&=&( x-1) ( x-2) \dfrac{1}{x-1} + ( x-1) ( x-2) \dfrac{7}{( x-1) ( x-2) } & {\color{#0066A7}{\hbox{Distribute on both sides.}}} \\ 3x-3&=&( x-2) +7 & {\color{#0066A7}{\hbox{Simplify.}}} \\ 3x-3&=&x+5 & \\ 2x&=&8\hbox{ } & \\ x&=&4 & \end{array} \] Since 4 is in the domain of the variable, the solution is \(4\).
(b) We group the terms of \(x^{3}-x^{2}-4x+4=0\), and factor by grouping. \[ \begin{array}{rclll} x^{3}-x^{2}-4x+4&=&0 & \\ [4pt] ( x^{3}-x^{2}) -( 4x-4) &=&0 & {\color{#0066A7}{\hbox{Group the terms.}}} \\[4pt] x^{2}( x-1) -4( x-1) &=&0 & {\color{#0066A7}{\hbox{Factor out the common factor}}} \\[-2pt] &&&{\color{#0066A7}{\hbox{from each group.}}}\\[4pt] ( x^{2}-4) ( x-1) &=&0 & {\color{#0066A7}{\hbox{Factor out the common factor \((x-1).\)}}} \\[4pt] ( x-2) ( x+2) ( x-1) &=&0 & {\color{#0066A7}{\hbox{\({x}^{2}-4=( {x-2}) ( {x+2})\)}}} \\[4pt] x-2=0\hbox{ or }x+2&=&0\hbox{ or }x-1=0 & {\color{#0066A7}{\hbox{Set each factor equal to 0.}}} \\[3pt] x\hbox{ }\,=\,\hbox{ }2\hbox{ }x&=&-2\hbox{ }x\hbox{ }\,=\,\hbox{ }1 & {\color{#0066A7}{\hbox{Solve.}}} \end{array} \] The solutions are \(-2\), 1, and 2.
CAUTION
Squaring both sides of an equation may lead to extraneous solutions. Check all apparent solutions.
(c) We square both sides of the equation since the index of a square root is \(2\). \[ \begin{array}{@{{-8pt}}rclll} \hbox{ }\sqrt{x-1}&=&x-7 & \\[4.5pt] ( \sqrt{x-1}) ^{2}&=& ( x-7) ^{2} & {\color{#0066A7}{\hbox{Square both sides.}}} \\[4.5pt] \hbox{}x-1&=&x^{2}-14x+49\hbox{} & \\[4.5pt] x^{2}-15x+50&=&0 & {\color{#0066A7}{\hbox{Put in standard form.}}} \\[4.5pt] ( x-10) ( x-5) &=&0 & {\color{#0066A7}{\hbox{Factor. }}} \\[4.5pt] \hbox{ }x=10\hbox{ or }x&=&5 & {\color{#0066A7}{\hbox{Set each factor equal to 0 and solve.}}} \end{array} \]
Check: \(x=10\): \(\sqrt{x-1}=\sqrt{10-1}=\sqrt{9}=3\) and \( x-7=10-7=3\)
\(x=5\): \(\sqrt{x-1}=\sqrt{5-1}=\sqrt{4}=2\) and \( x-7=5-7=-2\)
The apparent solution \(5\) is extraneous; the only solution of the equation is \(10\).
RECALL
\(\vert a\vert =a\) if \(a\geq 0\); \(\vert a\vert =-a\) if \(a<0\). If\( \vert x \vert =b\), \(b\geq 0\), then \(x=b\) or \(x=-b\).
(d) \begin{array}[t]{@{{-.8pc}}rclrcl@{\quad}l} \vert 1-x \vert &=&2 & & & \\[5pt] \hbox{ }1-x&=&2 & \hbox{or}\quad 1-x&=&-2 & {\color{#0066A7}{\hbox{The expression inside the absolute }}} \\[-2pt] &&&&&&{\color{#0066A7}{\hbox{value bars equals 2 or \(-2\).}}} \\[5pt] -x&=&1 & -x&=&-3 & {\color{#0066A7}{\hbox{Simplify.}}} \\[5pt] x&=&-1 & x&=&3 & {\color{#0066A7}{\hbox{Simplify.}}} \end{array} The solutions are \(-1\) and \(3\).
4 Solve InequalitiesPrinted Page A-5
A-5
In expressing the solution to an inequality, interval notation is often used.
NOTE
Every interval of real numbers contains both rational numbers, numbers that can be expressed as the quotient of two integers, and irrational numbers, numbers that are not rational.
DEFINITION
Let \(a\) and \(b\) represent two real numbers with \(a < b\).
A closed interval, denoted by \([ a,b] ,\) consists of all real numbers \(x\) for which \(a\leq x\leq b\).
An open interval, denoted by \(( a,b) \), consists of all real numbers \(x\) for which \(a < x < b\).
The half-open, or half-closed, intervals are:
- \(( a,b] \), consisting of all real numbers \(x\) for which \(a < x\leq b\), and
- \([ a,b) \), consisting of all real numbers \(x\) for which \(a\leq x < b\).
In each of these definitions, \(a\) is called the left endpoint and \( b\) the right endpoint of the interval.
The symbol \(\infty\) (read “infinity”) is not a real number, but a notational device used to indicate unboundedness in the positive direction. The symbol \(-\infty\) (read “negative infinity”) also is not a real number, but a notational device used to indicate unboundedness in the negative direction. Using the symbols \(\infty\) and \(-\infty \), we define five other kinds of intervals:
- \([ a,\infty ) ,\) consisting of all real numbers \(x\) for which \(x\geq a\)
- \(( a,\infty ) ,\) consisting of all real numbers \(x\) for which \(x > a\)
- \(( -\infty ,a]\), consisting of all real numbers \(x\) for which \(x\leq a\)
- \(( -\infty ,a)\), consisting of all real numbers \(x\) for which \(x < a\)
- \(( -\infty ,\infty ) \), consisting of all real numbers \(x\)
Notice that \(\infty\) and \(-\infty\) are never included as endpoints, since neither is a real number.
Table 1 summarizes interval notation, corresponding inequality notation, and their graphs.
Table 1
A-6
EXAMPLE 6Solving Inequalities
Solve each inequality and graph the solution:
(a) \(4x+7\geq 2x-3\)
(b) \(x^{2}-4x+3>0\)
(c) \(x^{2}+x+1 < 0\)
(d) \(\dfrac{1+x}{1-x}>0\)
Solution (a) \[ \begin{array}{@{\hspace*{-4pt}}rcll@{\quad}l} 4x+7&\geq& 2x-3 & & \\ 4x&\geq& 2x-10 & & {\color{#0066A7}{\hbox{Subtract 7 from both sides.}}} \\ 2x&\geq& -10 & & {\color{#0066A7}{\hbox{Subtract 2\(x\) from both sides.}}} \\ x&\geq& -5 & & {\color{#0066A7}{\hbox{Divide both sides by 2.}}}\quad \\ &&&&{\color{#0066A7}{\hbox{(The direction of the inequality symbol is unchanged.)}}} \end{array} \]
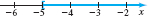
The solution using interval notation is \([ -5,\infty ) \). See Figure 1 for the graph of the solution.
NOTE
The test number can be any real number in the interval, but it cannot be an endpoint.
(b) This is a quadratic inequality. The related quadratic equation \(x^{2}-4x+3= ( x-1) ( x-3) =0\) has two solutions, \(1\) and \(3\). We use these numbers to partition the number line into three intervals. Now select a test number in each interval, and determine the value of \(x^{2}-4x+3\) at the test number. See Table 2.
Table 2
| Interval | Test Number | Value of \({x^{2}-4x}+{3}\) | Sign of \({x^{2}-4x}+ {3}\) |
|---|---|---|---|
| \( ( -\infty ,1)\) | \({0}\) | \({3}\) | Positive |
| \( (1,3)\) | \({2}\) | \({-1}\) | Negative |
| \(( 3,\infty )\) | \({4}\) | \({3}\) | Positive |

We conclude that \(x^{2}-4x+3>0\) on the set \(( -\infty ,1) \cup ( 3,\infty) \). See Figure 2 for the graph of the solution.
(c) The quadratic equation \(x^{2}+x+1=0\) has no real solution, since its discriminant is negative. [See Example 4(b)]. When this happens, the quadratic inequality is either positive for all real numbers or negative for all real numbers. To see which is true, evaluate \(x^{2}+x+1\) at some number, say, \(0\). At \(0,\) \(x^{2}+x+1=1,\) which is positive. So, \(x^{2}+x+1>0\) for all real numbers \(x\). The inequality \(x^{2}+x+1 < 0\) has no solution.
(d) The only solution of the rational equation \(\dfrac{1+x}{1-x} =0\) is \(x=-1;\) also, the expression \(\dfrac{1+x}{1-x}\) is not defined for \(x=1.\) We use the solution \(-1\) and the value \(1\), at which the expression is undefined, to partition the real number line into three intervals. Now select a test number in each interval, and evaluate the rational expression \(\dfrac{1+x}{1-x}\) at each test number. See Table 3.
Table 3
| Interval | Test Number | Value of \(\dfrac{{1}+{x}}{{1}-{x}}\) | Sign of \(\dfrac{{1}+{x}}{{1}-{x}}\) |
|---|---|---|---|
| \(( {-\infty ,-1})\) | \({-2}\) | \({-}\dfrac{1}{3}\) | Negative |
| \(( -{1,1})\) | \({0}\) | \({1}\) | Positive |
| \(( 1{,\infty })\) | \({2}\) | \(-3\) | Negative |

We conclude that \(\dfrac{1+x}{1-x}>0\) on the interval \(( -1,1)\). See Figure 3 for the graph of the solution.
Below we state an important relationship involving the absolute value of a sum.
A-7
NOTE
If \(x > 0\) and \(y > 0\), the Triangle Inequality is an algebraic statement for the fact that the length of any side of a triangle is less than the sum of the lengths of the other two sides.
THEOREM Triangle Inequality
If \(x\) and \(y\) are real numbers, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ |x+y| \leq |x| + |y|} } \]
Use the following theorem as a guide to solving inequalities involving absolute values.
THEOREM
If \(a\) is a positive number and if \(u\) is an algebraic expression, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{@{}l@{{-3pt}}} \vert u\vert < a \hbox{ is equivalent to } -\!a < u < a \quad(1)\\ \vert u\vert > a \hbox{ is equivalent to } u < -a \quad \hbox{or}\quad u > a \quad(2) \end{array} }} \]
Similar relationships hold for the nonstrict inequalities \(\vert u\vert \leq a\) and \(\vert u\vert \geq a.\)
EXAMPLE 7Solving Inequalities Involving Absolute Value
Solve each inequality and graph the solution:
(a) \(\vert 3-4x\vert < 11\)
(b) \(\vert 2x+4\vert -1\leq 9\)
(c) \( \left\vert \dfrac{4x+1}{2}-\dfrac{3}{5}\right\vert >1\)
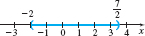
Solution (a) The absolute value is less than the number \(11,\) so statement (1) applies. \[ \begin{array}{@{{-4.5pc}}rcccc@{\quad}l} \vert 3-4x\vert &<&{11} & \\[3pt] -11 &<&3-4x&<&11&{\color{#0066A7}{\hbox{Apply statement (1).}}} \\[3pt] -14 &<&-4x&<&8 & {\color{#0066A7}{\hbox{Subtract 3 from each part.}}} \\[3pt] \dfrac{-14}{-4} &>&x&>&\dfrac{8}{-4} & {\color{#0066A7}{\raise5pt\hbox{Divide each part by \(-4\), which}}} \\[-9pt] &&&&&{\color{#0066A7}{\raise9pt\hbox{reverses the inequality signs.}}}\\[-5pt] -2 &<&x&<&\dfrac{7}{2} & {\color{#0066A7}{\hbox{Simplify and rearrange the ordering.}}} \end{array} \]
RECALL
Multiplying (or dividing) an inequality by a negative quantity reverses the direction of the inequality sign.
The solutions are all the numbers in the open interval \(\!\left( -2,\dfrac{7}{2}\right)\!\). See Figure 4 for the graph of the solution.
(b) We begin by putting \(\vert 2x+4\vert -1\leq 9\) into the form \(\vert u\vert \leq a\). \[ \begin{array}{@{{-4.7pc}}rclll@{\quad}l} \vert 2x+4\vert -1 &\leq &9 &\\[3pt] \vert 2x+4\vert &\leq &10 &&& {\color{#0066A7}{\hbox{Add 1 to each side.}}} \\[3pt] -10 &\leq &2x+4&\leq& 10 & {\color{#0066A7}{\hbox{Apply statement (1), but use \(\leq\).}}} \\[3pt] -14 &\leq &{2x}&\leq& 6 \\[3pt] -7 &\leq &{x}&\leq& 3 \end{array} \]
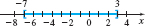
The solutions are all the numbers in the closed interval \([-7, 3]\) . See Figure 5 for the graph of the solution.
(c) \(\left\vert \dfrac{4x+1}{2}-\dfrac{3}{5}\right\vert > 1\) is in the form of statement (2). We begin by simplifying the expression inside the absolute value. \[ \left\vert \dfrac{4x+1}{2}-\dfrac{3}{5}\right\vert =\left\vert \dfrac{ 5( 4x+1) }{10}-\dfrac{2( 3) }{10}\right\vert =\left\vert \dfrac{20x+5-6}{10}\right\vert =\left\vert \dfrac{20x-1}{10} \right\vert \]
A-8
The original inequality is equivalent to the inequality below. \[ \left\vert \dfrac{20x-1}{10}\right\vert >1 \] \[ \begin{array}{@{{-2pc}}rcl@{\qquad}c@{\qquad}r@{\qquad}l} \dfrac{20x-1}{10} &<&-1 &\hbox{ or }& \dfrac{20x-1}{10}>1\hphantom{0} & {\color{#0066A7}{\hbox{Apply statement (2).}}} \\[8pt] 20x-1 &<&-10&\hbox{ or } &20x-1>10 \\[3pt] 20x &<&-9 &\hbox{ or }& 20x>11 \\[3pt] x\, &<&-\dfrac{9}{20} &\hbox{ or } & x>\dfrac{11}{20}\!\! \end{array} \]
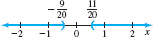
The solutions are all the numbers in the set \(\left( -\infty ,-\dfrac{9}{20}\right) \cup \left(\dfrac{11}{20},\infty \right) .\) See Figure 6 for the graph of the solution.
5 Work with ExponentsPrinted Page A-8
Integer exponents provide a shorthand notation for repeated multiplication. For example, \[ 2^{3}=2\cdot 2\cdot 2=8\quad \hbox{ or }\quad \left( \dfrac{1}{3}\right) ^{\!\!4}= \dfrac{1}{3}\cdot \dfrac{1}{3}\cdot \dfrac{1}{3}\cdot \dfrac{1}{3}=\dfrac{1}{81} \]
DEFINITION
If \(a\) is a real number and \(n\) is a positive integer, then the symbol \(a^{n}\) represents the product of \(n\) factors of \(a\). That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ a^{n}=\underset{\hbox{\(n\) factors}}{\underbrace{a\cdot a \cdot \ldots \cdot a}}}} \]
Here, it is understood that \(a^{1}=a\).
Then \(a^{2}=a\cdot a\) and \(a^{3}=a\cdot a\cdot a\), and so on. In the expression \(a^{n},\) the number \(a\) is called the base and the number \(n\) is called the exponent or power. We read \( a^{n}\) as “\(a\) raised to the power \(n\)” or as “\(a\) to the \(n\)th power.” We usually read \(a^{2}\) as “\(a\) squared” and \(a^{3}\) as “\(a\) cubed.”
DEFINITION
If \(a\neq 0\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ a^{0}=1 }}\]
If \(n\) is a positive integer, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ a^{-n}=\dfrac{1}{a^{n}}\qquad a\neq 0 }}\]
The following properties, called the Laws of Exponents, can be proved using the preceding definitions.
THEOREM Laws of Exponents
In each of these properties \(a\) and \(b\) are real numbers, and \(u\) and \(v\) are integers. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{rcl@{\quad}c@{\!\!\!\!\!\quad}c@{\,\,\qquad\qquad}rcll} a^{u}a^{v}&=&a^{u+v} && ( a^{u})^{v}=a^{uv} & ( ab ) ^{u}&=&a^{u}b^{u} \\[6pt] \dfrac{a^{u}}{a^{v}}=a^{u-v}&=&\dfrac{1}{a^{v-u}} &\hbox{if }a\neq 0 &&\left( \dfrac{a}{b}\right) ^{u} &=&\dfrac{a^{u}}{b^{u}}_{\vphantom{0_0}} & {\rm \ if\ }b\neq 0 \end{array} }} \]
A-9
IN WORDS
The symbol \(\sqrt[{n}]{a}\) means “the number that, when raised to the \(n\)th power, equals \(a\).”
DEFINITION
The principal \(n{\rm th}\) root of a real number \(a\), where \(n\geq 2\) is an integer, symbolized by \(\sqrt[{ n }]{a}\), is defined as the solution of the equation \(b^{n}=a.\) \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sqrt[{ n}]{a}=b \hbox{ is equivalent to } a=b^{n} }} \]
If \(n\) is even, then both \(a\geq 0\) and \(b\geq 0,\) and if \(n~\) is odd, then \(a\) and \(b\) are any real numbers and both have the same sign.
If \(a\) is negative and \(n\) is even, then \(\sqrt[{ n}]{a}\) is not defined. When \(\sqrt[{ n}]{a}\) is defined, the principal \(n{\rm th}\) root of a number is unique.
The symbol \(\sqrt[{ n}]{a}\) for the principal \(n{\rm th}\) root of \(a\) is called a radical; the integer \(n\) is called the index, and \(a\) is called the radicand. If the index of a radical is \(2\), we call \(\sqrt[2]{a}\) the square root of \(a\) and omit the index \(2\) by writing \(\sqrt{a}\). If the index is 3, we call \(\sqrt[3]{a}\) the cube root of \(a\).
Radicals are used to define rational exponents.
DEFINITION
If \(a\) is a real number and \(n\geq 2\) is an integer, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ a^{1/n}=\sqrt[{ n}]{a}} } \] provided that \(a^{1/n}=\sqrt[n]{a}\) exists.
DEFINITION
If \(a\) is a real number and \(m\) and \(n\) are integers with \(n\geq 2,\) then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ a^{m/n}= ( a^{1/n}) ^{m} }} \] provided that \(\sqrt[{ n}]{a}\) exists.
From the two definitions, we have \[ a^{m/n}=\sqrt[{ n}]{a^{m}}=( \sqrt[{ n}]{a}) ^{m} \]
In simplifying the rational expression \(a^{m/n}\), either \(\sqrt[{ n}]{ a^{m}}\) or \(( \sqrt[{ n}]{a}) ^{m}\) can be used. The choice depends on which is easier to simplify. Generally, taking the root first, as in \(( \sqrt[n]{a}) ^{m}\), is easier.
But does \(a^{x}\) have meaning, where the base \(a\) is a positive real number and the exponent \(x\) is an irrational number? The answer is yes, and although a rigorous definition requires methods discussed in calculus, the basis for the definition is easy to follow: Select a rational number \(r\) that is formed by truncating (removing) all but a finite number of digits from the irrational number \(x\). Then it is reasonable to expect that \[ a^{x}\,{\approx}\,a^{r} \]
For example, take the irrational number \(\pi =3.14159\ldots.\) Then an approximation to \(a^{\pi }\) is \[ a^{\pi}\,{\approx}\,a^{3.14} \]
where the digits after the hundredths position have been truncated from the value for \(\pi .\) A better approximation would be \[ a^{\pi}\,{\approx}\,a^{3.14159} \]
where the digits after the hundred-thousandths position have been truncated. Continuing in this way, we can obtain approximations to \(a^{\pi }\) to any desired degree of accuracy.
It can be shown that the Laws of Exponents hold for real number exponents \(u\) and \(v.\)
6 Work with LogarithmsPrinted Page A-10
A-10
The definition of a logarithm is based on an exponential relationship.
DEFINITION
Suppose \(y=a^{x}\!\), \(a>0\), \(a\neq 1\), and \(x\) is a real number. The logarithm with base \( a\) of \( y\), symbolized by \(\log _{a} y,\) is the exponent to which \(a\) must be raised to obtain \(y.\) That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \log _{a} y=x \hbox{ is equivalent to } y=a^{x} } }\]
As this definition states, a logarithm is a name for a certain exponent.
EXAMPLE 8Working with Logarithms
(a) If \(x=\log _{3}y\), then \(y=3^{x}\). For example, \(4=\log _{3}81\) is equivalent to \(81=3^{4}\).
(b) If \(x=\log _{5}y\), then \(y=5^{x}\). For example, \[ -1=\log _{5}\!\left(\dfrac{1}{5}\right) \hbox{ is equivalent to } \dfrac{1}{5}=5^{-1} \]
THEOREM Properties of Logarithms
In the properties given next, \(u\) and \(a\) are positive real numbers, \( a \neq 1\), and \(r\) is any real number. The number \(\log _{a} u\) is the exponent to which \(a\) must be raised to obtain \(u\). That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ a^{\log _{a} u}=u }} \]
The logarithm with base \(a\) of \(a\) raised to a power equals that power. That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \log _{a} a^{r}=r }}\]
EXAMPLE 9Using Properties of Logarithms
(a) \(2^{\log _{2}\pi }=\pi\)
(b) \(\log _{0.2} 0.2^{(-\sqrt{2})}=-\sqrt{2}\)
(c) \(\log _{1/5}\! \left( \dfrac{1}{5}\right) ^{\!\!kt}=kt\)
THEOREM Properties of Logarithms
In the following properties, \(u\), \(v\), and \(a\) are positive real numbers, \(a\neq 1\), and \(r\) is any real number:
- The Log of a Product Equals the Sum of the Logs \[ \fbox{\({ \log _{a}( uv) =\log _{a}u+\log _{a}v}\)}\tag{3} \]
- The Log of a Quotient Equals the Difference of the Logs \[ \fbox{\({ \log _{a}\!\left( \dfrac{u}{v}\right) =\log _{a}u-\log _{a}v }\)}\tag{4} \]
- The Log of a Power Equals the Product of the Power and the Log \[ \fbox{\({ \log _{a}u^{ r}=r\log _{a}u }\)}\tag{5} \]
EXAMPLE 10Using Properties (3), (4), and (5) of Logarithms
(a) \( \begin{array}{@{}rcll@{\quad}lcl} \log _{a} \big( x\displaystyle\sqrt{x^{2}+1} \big) &=&\log _{a}x+\log _{a}\displaystyle\sqrt{x^{2}+1} & & {\color{#0066A7}{\log _{a} ({uv})}}{\color{#0066A7}{=}}\,{\color{#0066A7}{\log _{a}u+\log_av}} \\[3pt] &=&\log _{a}x+\log _{a}( x^{2}+1) ^{1/2} & & \\[2pt] &=&\log _{a}x+\dfrac{1}{2}\log _{a}( x^{2}+1) & & {\color{#0066A7}{\log_{a}{u}^{r}}}{\color{#0066A7}{=}}\,{\color{#0066A7}{r\log _{a}u}} \end{array} \)
A-11
(b)
(c) \( \begin{array}[t]{lll} \log _{a}x+\log _{a}9+\log _{a}( x^{2}+1) -\log _{a}5 & =\log _{a} (9x) +\log _{a}( x^{2}+1) -\log _{a}5 & \\[5pt] & =\log _{a} [ 9x( x^{2}+1)] -\log _{a}5 & \\[5pt] & =\log _{a}\!\left[ \dfrac{9x( x^{2}+1) }{5}\right] \end{array} \)
CAUTION
In using properties (3) through (5), be careful about the values that the variable may assume. For example, the domain of the variable for \(\log _{a}{x}\) is \({x>0}\), and for \(\log _{a}( {x-1})\) it is \({x>1}\). That is, the equality \(\log _{a} x+\log _{a}(x-1) =\log _{a} [{x}({x-1})]\) is true only for \({x>1}\).
CAUTION Common errors made by some students include:
- Expressing the logarithm of a sum as the sum of the logarithms.
\(\log _{a} ( u+v)\) is not equal to \(\log _{a}u+\log _{a}v\) Correct statement: \(\log _{a}( uv) =\log _{a}u+\log_{a}v\) Property (3) - Expressing the difference of logarithms as the quotient of logarithms.
\(\log _{a}u-\log _{a}v\) is not equal to \(\dfrac{\log _{a}u}{\log _{a}v}\) Correct statement: \(\log _{a}u-\log _{a}v=\log _{a}\!\left( \dfrac{u}{v}\right)\) Property (4) - Expressing a logarithm raised to a power as the product of the power and the logarithm.
\( ( \log _{a} u) ^{r}\) is not equal to \(r\log _{a}u\) Correct statement: \(\log _{a} u^{r}=r\log _{a}u\) Property (5)
Since most calculators can calculate only logarithms with base \(10,\) called common logarithms and abbreviated log, and logarithms with base \(e\approx 2.718,\) called natural logarithms and abbreviated ln, it is often useful to be able to change the bases of logarithms.
THEOREM Change-of-Base Formula
If \(a\neq 1,\) \(b\neq 1\), and \(u\) are positive real numbers, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \log _{a}u=\dfrac{\log _{b}u}{\log _{b}a}}} \]
For example, to approximate \(\log _{2}15,\) we use the change-of-base formula. Then we use a calculator. \begin{eqnarray*} \log _{2}15 \underset{\underset{\color{#0066A7}{\hbox{Change-of-Base Formula}}}{\color{#0066A7}{\uparrow }}} {=} \dfrac{\log 15}{\log 2}\approx 3.907\\[-10pt] \end{eqnarray*}
