Chapter 2
Section 2.1
1. True
2. True
3. Prime, slope, (c, f (c))
4. True
5. 6
6. derivative
7.
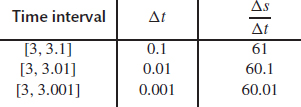
The velocity appears to approach 60 cm/s.
9. v(t) = 4 m/s at t = 0, v(t) = 16 m/s at t = 2, v(t) = 6t0 + 4 m/s at any t0
11. v(1) = 7 cm/s, v(4) =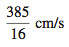 
13. y = −12x – 12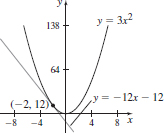
15. y = 12x + 16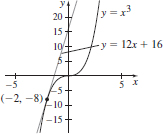
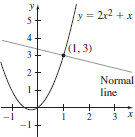
17. y = −x + 2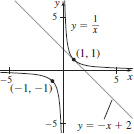
19. y =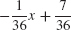 
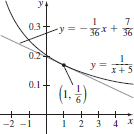
21. y =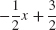 
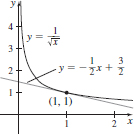
23. (a) 5
(b) 5
(c) 5
25. (a) 0
(b)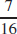 
(c)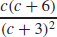 
27. f′(1) = 2
29. f′(0) = 0
31. f′(−1) = −5
33. f′(4) = 
35. f′(0) = −7
37. (a) 7 ≤ t ≤ 10 and 11 ≤ t ≤ 13
(b) 0 ≤ t ≤ 4
(c) 4 ≤ t ≤ 7 and 10 ≤ t ≤ 11
(d) Average speed ≈ 0.675 mi/min
(e) 0.415 mi/min
39. −3
41. No
43. R′(50) = 0.59
45. (a) 250 sales per day
(b) 200 sales per day
47. (a) 32 ft/s
(b) t ≈ 7.914 s
(c) Average velocity ≈ 126.618 ft/s
(d) v(7.914) ≈ 253.235 ft/s
49. (a) 9.8 m/s
(b) t ≈ 4.243 s
(c) Average velocity ≈ 20.789 m/s
(d) v(4.243) ≈ 41.578 m/s
51. (a)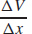 
≈ 12.060 cm3/cm
(b) V′(2) = 12 cm3/cm
53. f′(x) = 2ax +b
55. (a) d′(t) is the rate of change of diameter (in centimeters) with respect to time (in days).
(b) d′(1) > d′(20)
(c) d′(1) is the instantaneous rate of change of the peach’s diameter on day 1 and d′(20) is the instantaneous rate of change of the peach’s diameter on day 20.
Section 2.2
1. False
2. False
3. (b)Vertical
4. derivative
5. 0
7. 2
9. −2c
11. f′(x) = 0, all real numbers
13. f′(x) = 6x+1, all real numbers
15. f′(x) =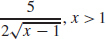 
17. f′(x) = 
19. f′(x) = 4x – 5
21. f′(x) = 3x2 − 8
23. Not a graph of f and f′
25. Graph of f and f′. The black curve is the graph of f; the gray curve is the graph of f′.
27. 
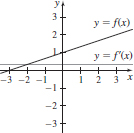
29. 
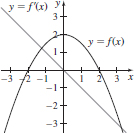
31. (B)
33. (A)
35. f′(−8) =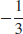 
37. f′(2) does not exist.
39. f′(1) = 2
41. 
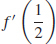does not exist.
43. f′(−1) does not exist.
45. (a) −2 and 4
(b) 0, 2, 6
47. (a) u′1(1) does not exist.
(b) u1 (t) models a switch that is off when t < 1 and on when t ≥ 1.
49. f′(x) = m
51. f′(x) = −2/x3
53. f (x) = x2, c = 2
55. f (x) = x2, c = 1
57. f (x) = sin x, c =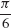 
59. f (x) = 2(x + 2)2 − (x + 2), c = 0
61. (a) Continuous at 0
(b) f′(0) = 0
(c)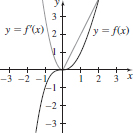
63. (a) s′(4.99) = 74.7003 ft/s; s′(5.01) = 0 ft/s
(b) Not continuous
(c) Answers will vary.
65. 
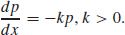
67. 
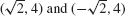
69. (a) 2πr(Δr)+π(Δr)2
(b) 2πΔr
(c) 2πr +πΔr
(d) 2π
(e) 2π
71. See Student Solutions Manual.
73. See Student Solutions Manual.
75. (a) Parallel
(b) Perpendicular
77. (a) k = 4
(b) f′(3) = 12
(c) f′(x) = 4x
Section 2.3
1. 0; 3x2
2. nxn−1
3. True
4. 
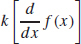
5. ex
6. True
7. f′(x) = 3
9. f′(x) = 2x + 3
11. f′(u) = 40u4 − 5
13. f′(s) = 3as2 + 3s
15. f′(t) =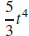 
17. f′(t) =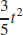 
19. f′(x) =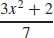 
21. f′(x) = 2ax + b
23. f′(x) = 4ex
25. f′(u) = 10u − 2eu
27. 
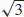
29. 2π R
31. 4πr2
33. (a) 3
(b) y = 3x − 1
(c)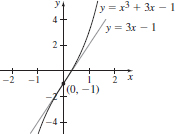
35. (a) 6
(b) y = 6x + 1
(c)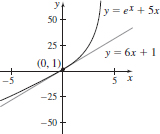
37. (a) (2,−8)
(b) y = −8
(c) x > 2
(d) x < 2
(e)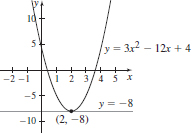 
(f) f is increasing when x = 2 and decreasing when x < 2.
39. (a) None
(b) None
(c) All real numbers
(d) None
(e)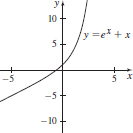 
(f) f is increasing for all x.
41. (a) (1, 0), (−1, 4)
(b) y = 0, y = 4
(c) x < −1 or x = 1
(d) −1 < x < 1
(e)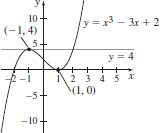 
(f) f is increasing when x < −1 or x > 1 and decreasing when −1 < x < 1.
43. v(0) = −1 m/s and v(5) = 74 m/s
45. (a) v(t) = 2t − 5
(b) t = 
47. (a) 
(b)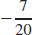 
(c)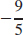 
(d)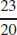 
(e)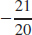 
(f)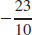 
49. (a) f′(x) = 24x2 − 24x + 6
(b) f′(x) = 6(2x − 1)2
51. 
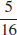
53. 20480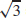 
55. 3ax2
57. y = 5x − 3
59. y = x + 1
61. y =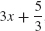 
, y = 3x −9
63. (a) y = 45x – 65
(b)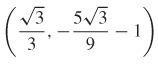 
, 
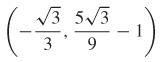
(c)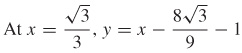 
and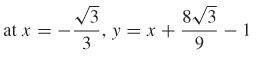 
(d)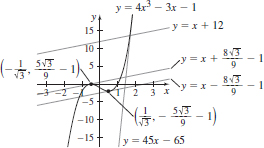
65. See Student Solutions Manual.
67. See Student Solutions Manual.
69. a = 3, b = 2, c = 0
71. (2, 4)
73. (a) 0
(b) −kR
(c) −2kR
75. (a)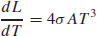 
(b) 2.694 × 1023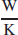 
(c) 2.694 × 1023 w
77. F′(x) = mx
79. See Student Solutions Manual.
81. 
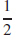
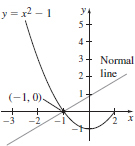
83. 
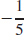
85. −4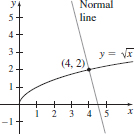
87. Q =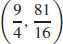 
89. y =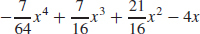 
91. (a) c = 1
(b) y = 12x − 16 and y = 12x + 1
Section 2.4
1. False
2. f (x)g′(x) + f′(x)g(x)
3. False
4. 
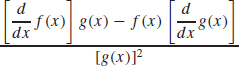
5. True
6. 
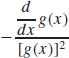
7. 0
8. 
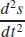
9. f′(x) = ex (x + 1)
11. f′(x) = 5x4 − 2x
13. f′(x) = 18x2 + 6x – 10
15. s′(t) = 16t7 − 24t5 + 10t4 − 4t3 + 4t − 1
17. f′(x) = x3ex + 3x2ex + ex + 3x2
19. g′ (s) =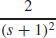 
21. G′ (u) =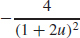 
23. f′(x) =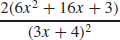 
25. f′(w) =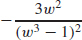 
27. s′(t) =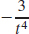 
29. f′(x) =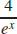 
31. f′(x) =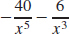 
33. f′(x) = 9x2 +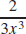 
35. s′(t) =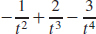 
37. f′(x) =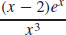 
39. f′(x) =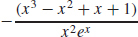 
41. f′(x) = 6x + 1, f″(x) = 6
43. f′(x) = f″(x) = ex
45. f′(x) = ex(x + 6), f″(x) = ex(x + 7)
47. f′(x) = 8x3 + 3x2 + 10, f″(x) = 24x2 + 6x
49. f′(x) =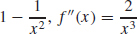 
51. f′(t) =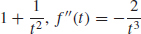 
53. f′(x) =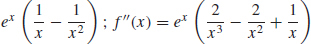 
55. (a) y′ =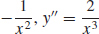 
(b) y′ =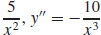 
57. v(t) = 32t + 20, a(t) = 32
59. v(t) = 9.8t + 4, a(t) = 9.8
61. f(4)(x) = 0
63. 5040
65. eu
67. −ex
69. (a)
(b)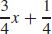 
(c) (0, 0), (2, 4)
(d)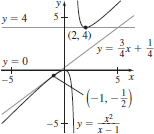
71. (a)
(b) y =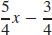 
(c) (0, 0),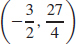 
(d)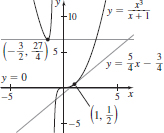
73. (a) (−2, 5), (2,−27)
(b) y = 5, y = −27
(c) x < −2 or x > 2
(d) −2 < x < 2
(e)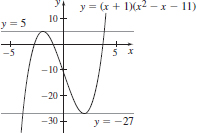
75. (a) (0, 0), (−2,−4)
(b) y = 0, y = −4
(c) x < −2 or x > 0
(d) −2 < x < −1 or −1 < x < 0
(e)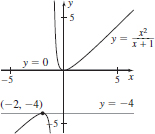
77. (a) (−1,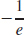 
)
(b) y =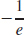
(c) x > −1
(d) x < −1
(e)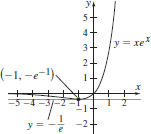
79. (a) (−1,−2e), (3,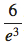 
)
(b) y = −2e, y =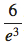
(c) −1 < x < 3
(d) x < −1 or x > 3
(e)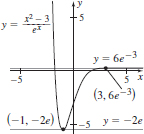
81. (a)
(b)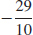 
(c) 
(d)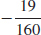 
(e) 
(f)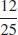 
83. (a) v(t) = −9.8t + 39.2
(b) t = 4 seconds
(c) 78.4 m
(d) −9.8 m/s2
(e) t = 8 s
(f) v = −39.2 m/s
(g) 156.8 m
85. (a) 0 ≤ x ≤ 100
(b)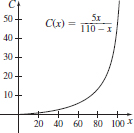 
(c) $13,333.33
(d) C′(x) =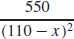 
(e) C′(40) = 0.112 = $112/%, C′(60) = 0.220 = $220/%, C′(80) = 0.611 = $611/%, C′(90) = 1.375 = $1,375/%
(f) Answers will vary.
87. (a)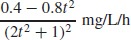 
(b)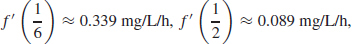 
, f′(1) ≈ −0.044 mg/Lh
(c) Answers will vary.
(d)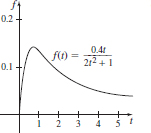 
(e) Concentration is highest at approximately 45 min and is about 0.14 mg/L.
89. (a)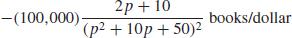 
(b) D′(5) = −128, D′(10) = −48, D′(15) = −22.145
91. (a)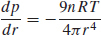 
(b) As the radius increases, pressure within the container decreases.
(c) p′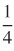
≈ −415945.358 Pa/m
93. (a) v(t) = 3t2 − 1, a(t) = 6t, J (t) = 6, S(t) = 0
(b) t = ±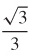
(c) a(2) = 12 m/s2, a(5) = 30 m/s2
(d) No
(e) Answers will vary.
95. (a) a(t) = 1.6 + 1.998t m/s2
(b) J (t) = 1.998 m/s3
97. (a)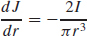 
(b) As radius increases, current density decreases.
(c) −1.273 × 1010 amps/m3
99. See Student Solutions Manual.
101. y′ = 6x5 − 5x4 + 20x3 − 18x2 + 2x − 5
103. y′ = 9x2 (x3 + 1)2
105. 
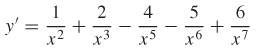
107. See Student Solutions Manual.
109. 
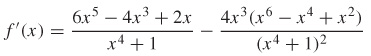
111. (a) f′(x) =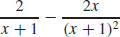 
(b) f′(x) =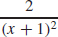 
(c) f(5)(x) =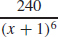 
113. (a)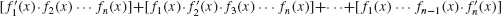 
(b)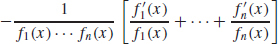 
115. (a) f1(x) =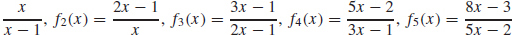 
(b) a0 = 1, a1 = 1, a2 = 2, a3 = 3, a4 = 5, a5 = 8
(c) an+2 = an+1 + an
(d)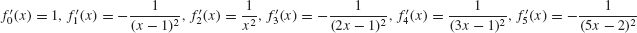 
Section 2.5
1. False
2. False
3. True
4. False
5. f′(π) = 2
7. f′(π/3) =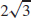 
9. y′ = 3 cos θ + 2 sin θ
11. y′ = cos2 x − sin2 x = cos 2x
13. y′ = cos t − t sin t
15. y′ = ex (sec2 x + tan x)
17. y′ = π sec u (sec2 u + tan2 u)
19. 
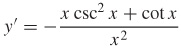
21. y′ = x(x cos x + 2 sin x)
23. \(y'=t\sec^{2}t+\tan t-\sqrt{3}\sec t\tan t\)
25. 
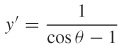
27. y′ = (cos t + t cos t − sin t)/(1 + t)2
29. y′ = (cos x − sin x)/ex
31. y′ = −2/(sin θ − cos θ)2
33. y′ = (sec t tan t + t tan2 t − t − tan t)/(1 + t sin t)2
35. y′ = −csc θ(csc2 θ + cot2 θ)
37. y′ = 2 sec2 x/(1 − tan x)2
39. y″ = −sin x
41. y″ = 2 tan θ sec2 θ
43. y″ = 2 cos t − t sin t
45. y″ = 2ex cos x
47. y″ = 3 cos u − 2 sin u
49. y″ = −(a sin x + b cos x)
51. (a) y = x
(b)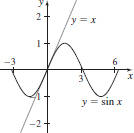
53. (a) y = x
(b)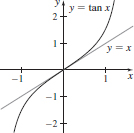
55. (a) y =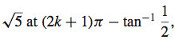 
(b)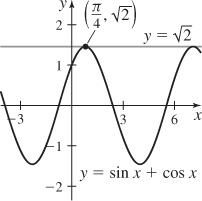
57. (a) {(tan−1 2+2nπ,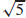 
)}, {(tan−1 2+(2n +1)π,−
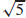)}, where n is an integer
(b)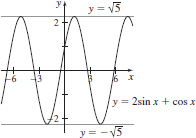
59. (a) {(2nπ, 1)}, {((2n + 1)π,−1)}, where n is an integer
(b)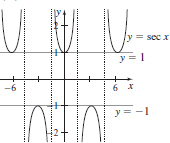 
61. f(n)(x) =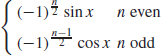 
63. −1
65. (a) v(t) =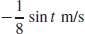 
(b)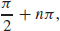 
+ nπ, where n is an integer
(c) a(t) =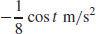 
(d)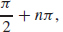 
, where n is an integer
(e)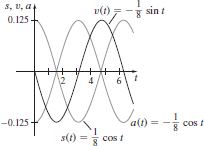
67. (a)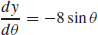 
(b)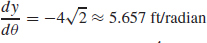 
69. (a)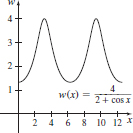 
(b) Max = 4, Min = 
(c) x = π, 2π, 3π
(d) w(π − 0.1) ≈ 0.395, w(2π − 0.1) ≈ −0.045
(e) Answers will vary.
71. (a) $10,000, $25,093, $15,411, $37,570
(b) R(t) = cos t + 0.3
(c) 10,540 dollars/2-months
(d)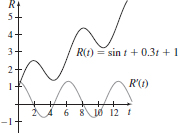 
(e) Answers will vary.
73. n = 4
75. See Student Solutions Manual.
77. See Student Solutions Manual.
79. See Student Solutions Manual.
81. See Student Solutions Manual.
Review Exercises
1. (a) 
(b) 
(c)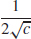 
3. 2
5. 5
7. 2
9. f′(x) = 1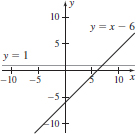
11. f′(x) =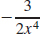 
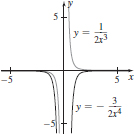
13. Does not have a derivative at c = 1.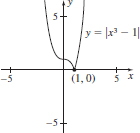
15. Not the graph of a function and its derivative.
17. 
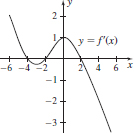
19. f′(x) = 5x4
21. f′(x) = x3
23. f′(x) = 4x – 3
25. F′(x) = 14x
27. f′(x) = 15(x2 − 6x + 6)
29. f′(x) =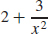 
31. f′(x) =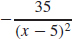 
33. f′(x) =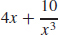 
35. f′(x) =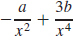 
37. f′(x) =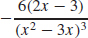 
39. s′(t) =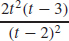 
41. F′(z) =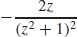 
43. g′(z) =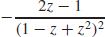 
45. s′(t) = −et
47. f′(x) =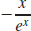 
49. f′(x) = x cos x + sin x
51. G′(u) = sec u(sec u + tan u)
53. f′(x) = ex(cos x +sin x)
55. f′(x) = 2(cos2 x −sin2 x) = 2 cos (2x)
57. f′(x) = 2 cos x sin x = sin (2x)
59. f′(θ) =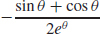 
61. f′(x) = 50x + 30, f″;(x) = 50
63. g′(u) =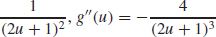 
65. f′(u) =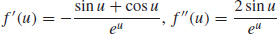 
67. (a) y = −7x + 5
(b)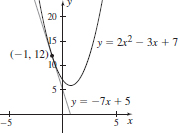
69. (a) y = −x − 1
(b)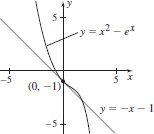
71. (a) v(0) = −6 m/s, v(5) = 4 m/s, v(t) = 2t − 6 m/s
(b) a(t) = 2 m/s2
73. (a)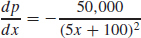
(b) R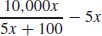(x) = 
− 5x
(c) R′(10) =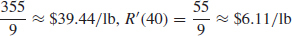 
75. f′(3) does not exist.
77. 8x − 16, f (x) = (4 − 2x)2