1.6 The ε-δ Definition of a Limit
Printed Page 130
OBJECTIVES
When you finish this section, you should be able to:
Throughout the chapter, we stated that we could be sure a limit was correct only if it was based on the \(\epsilon \)-\(\delta \) definition of a limit. In this section, we examine this definition and how to use it to prove a limit exists, to verify the value of a limit, and to show that a limit does not exist.
Consider the function \(f\) defined by \begin{equation*} f(x)=\left\{ {{ \begin{array}{c@{\qquad}l} {3x+1} & \hbox{if }{x\neq 2} \\[3pt] 10 & \hbox{if }{x=2} \end{array} }}\right. \end{equation*}
whose graph is given in Figure 64.
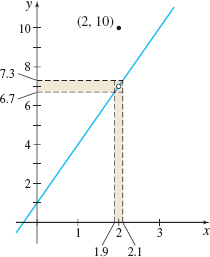
As \(x\) gets closer to \(2\), the value \(f(x)\) gets closer to \(7\). If in fact, by taking \(x\) close enough to \(2,\) we can make \(f(x)\) as close to \(7\) as we please, then \(\lim\limits_{x\rightarrow 2}f(x)=7\).
Suppose we want \(f(x)\) to differ from \(7\) by less than \(0.3\); that is, \begin{equation*} \begin{array}{rcl} -0.3& \lt &f(x)-7 \lt 0.3 \\ 6.7& \lt &f(x) \lt 7.3 \end{array} \end{equation*}
How close must \(x\) be to \(2\)? First, we must require \(x\neq 2\) because when \(x=2\), then \(f(x)=f(2)=10\), and we obtain \(6.7 \lt 10 \lt 7.3\), which is impossible.
131
Then, when \(x\neq 2\),
\(-0.3\lt f(x)-7 \lt 0.3\)
\(-0.3\lt (3x+1)-7 \lt 0.3\)
\(-0.3\lt 3x-6 \lt 0.3\)
\(-0.3\lt 3(x-2) \lt 0.3\)
\(\dfrac{-0.3}{3}\lt x-2 \lt \dfrac{0.3}{3}\)
\(-0.1\lt x-2 \lt 0.1\)
\(\vert x-2\vert \lt 0.1\)
That is, whenever \(x\neq 2\) and \(x\) differs from \(2\) by less than \(0.1,\) then \(f( x) \) differs from \(7\) by less than \(0.3\).
Now, generalizing the question, we ask, for \(x\neq 2\), how close must \(x\) be to \(2\) to guarantee that \(f(x)\) differs from \(7\) by less than any given positive number \(\epsilon ?\) (\(\epsilon \) might be extremely small.) The statement “\(f(x)\) differs from \(7\) by less than \(\epsilon \)” means \begin{equation*} \begin{array}{rcl} -\epsilon &\lt&f(x)-7 \lt \epsilon \\[3pt] 7-\epsilon &\lt&f(x) \lt 7+\epsilon \qquad {\color{#0066A7}{\hbox{Add 7 to each expression.}}} \end{array} \end{equation*}
When \(x\neq 2,\) then \(f(x)=3x+1\), so \begin{equation*} 7-\epsilon \lt 3x+1 \lt 7+\epsilon\ \end{equation*}
Now we want the middle term to be \(x-2.\) This is done as follows: \begin{equation*} \begin{array}{r@{\qquad}ll} 7-\epsilon \lt 3x+1\lt 7+\epsilon &\\[12pt] 6-\epsilon \lt 3x<6+\epsilon & {\color{#0066A7}{\hbox{Subtract 1 from each expression.}}}\\[12pt] 2-\frac{\epsilon }{3} \lt x\lt 2+\frac{\epsilon }{3} & {\color{#0066A7}{\hbox{Divide each expression by 3.}}}\\[12pt] -\frac{\epsilon }{3} \lt x-2\lt \frac{\epsilon }{3} & {\color{#0066A7}{\hbox{Subtract 2 from each expression.}}}\\[12pt] \vert x-2\vert \lt \dfrac{\epsilon }{3} & \end{array} \end{equation*}
The answer to our question is
“ \(x\) must be within \(\dfrac{\epsilon^{\vphantom{\vrule height2pt width0pt depth0pt}} }{3_{\vphantom{\vrule height1.7pt width0pt depth0pt}}}\) of \(2\), but not equal to \(2\), to guarantee that \(f(x)\) is within \(\epsilon \) of \(7\)”
That is, whenever \(x\neq 2\) and \(x\) differs from \(2\) by less than \(\dfrac{\epsilon }{3}\), \(x\neq 2,\) then \(f(x)\) differs from \(7\) by less than \( \epsilon \), which can be restated as \begin{equation*} \hbox{whenever }\left[ \begin{array}{c} x\neq 2\hbox{ and }x\hbox{ differs from }2 \\[5pt] \hbox{by less than }\delta =\dfrac{\epsilon }{3} \end{array} \right]\qquad \hbox{ then }\left[ \begin{array}{c} f(x)\hbox{ differs from }7 \\ \hbox{by less than }\epsilon \end{array} \right] \hbox{ } \end{equation*}
Notation is used to shorten the statement. We shorten the phrase ”\( \epsilon \) is any given positive number” by writing \(\epsilon >0.\) Then the statement on the right is written \begin{equation*} \left\vert f(x)-7\right\vert \lt \epsilon \end{equation*}
Similarly, the statement “\(x\) differs from \(2\) by less than \(\delta \)” is written \(\vert x-2\vert \lt \delta \). The statement “\(x\neq 2\)” is handled by writing \begin{equation*} 0 \lt \vert x-2\vert \lt \delta \end{equation*}
132
So for our example, we write
Given any \(\epsilon \gt0\), then there is a number \(\delta >0\) so that \[ \hbox{whenever } 0 \lt \vert x-2\vert \lt \delta , \hbox{then } \vert f(x)-7\vert \lt \epsilon \]
Since the number \(\delta =\dfrac{\epsilon }{3}\) satisfies the inequalities for any number \(\epsilon >0\), we conclude that \( \lim\limits_{x\rightarrow 2}f(x)=7\).
This discussion explains the definition of the limit of a function given below.
NOW WORK
DEFINITION Limit of a Function
Let \(f\,\) be a function defined everywhere in an open interval containing \(c\), except possibly at \(c\). Then the limit as \({x}\) approaches \({c}\) of \({f(x)}\) is \({L}\), written \[\bbox[5px, border:1px solid black, #F9F7ED]{ \lim\limits_{x\rightarrow c}f(x)=L} \]
if given any number \(\epsilon >0\), there is a number \(\delta >\) \(0\) so that \[\bbox[5px, border:1px solid black, #F9F7ED]{ \hbox{whenever\(\,\ \ 0 \lt \vert x-c\vert \lt \delta \) then \(\vert f(x)-L\vert \lt \epsilon \)}} \]
This definition is commonly called the \({\epsilon}\) - \({\delta}\) definition of a limit of a function.
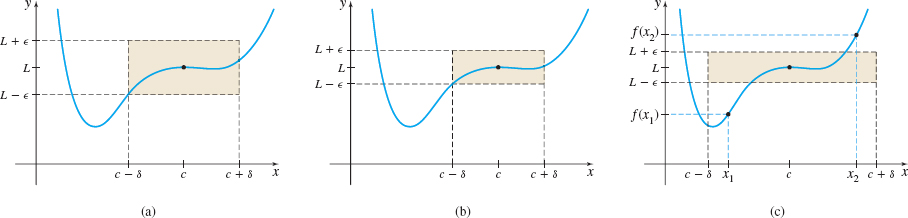
Figure 65 illustrates the definition for three choices of \(\epsilon \). Compare Figures 65(a) and 65(b). Notice that in Figure 65(b), the smaller \( \epsilon \) requires a smaller \(\delta \). Figure 65(c) illustrates what happens if \(\delta \) is too large for the choice of \(\epsilon \); here there are values of \(f\), for example, at \(x_{1}\) and \(x_{2},\) for which \( \vert f(x)-L\vert \nless \epsilon .\)
1 Use the ε-δ Definition of a Limit
Printed Page 132
EXAMPLE 1Using the \(\epsilon \)-\(\delta\) Definition of a Limit
Use the \(\epsilon \)-\(\delta \) definition of a limit to prove \( \lim\limits_{x\rightarrow -1} (1-2x) =3\).
Solution Given any \(\epsilon \gt0\), we must show there is a number \(\delta \gt0\) so that \begin{equation*} \hbox{whenever }\quad 0 \lt \vert x-(-1) \vert \lt \delta \qquad \hbox{then }\vert ( 1-2x) -3\vert \lt \epsilon \end{equation*}
The idea is to find a connection between \(\vert x-(-1)\vert =|x+1|\ \) and \(\vert ( 1-2x) -3\vert \). Since \begin{equation*} \vert (1-2x)-3\vert =\vert -2x-2\vert = \vert -2(x+1)\vert = \vert -2\vert \cdot \vert x+1\vert =2\vert x+1\vert \end{equation*}
we see that for any \(\epsilon >0,\) \begin{equation*} \hbox{whenever}\quad \vert x-(-1)\vert =\vert x+1\vert \lt \dfrac{\epsilon }{2}\qquad \hbox{ then }\vert (1-2x)-3\vert \lt \epsilon \hbox{ } \end{equation*}
133
That is, given any \(\epsilon \gt 0\) there is a \(\delta,\delta =\dfrac{\epsilon}{2}\), so that whenever \(0 \lt \vert x-(-1)\vert \lt \delta\), we have \(\vert (1-2x)-3\vert \lt \epsilon \). This proves that \(\lim\limits_{x\rightarrow -1}(1-2x)=3\).
NOW WORK
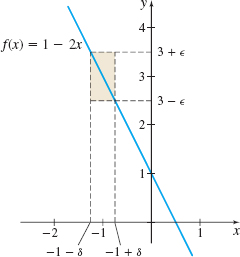
A geometric interpretation of the \(\epsilon \)-\(\delta\) definition is shown in Figure 66. We see that whenever \(x\) on the horizontal axis is between \(-1-\delta\) and \(-1+\delta\), but not equal to \(-1,\) then \(f(x)\) on the vertical axis is between the horizontal lines \(y=3+\epsilon \) and \( y=3-\epsilon .\) So, \(\lim\limits_{x\rightarrow -1}f(x)=3\) describes the behavior of \(f\) near \(-1\).
EXAMPLE 2Using the \(\epsilon \)-\(\delta\) Definition of a Limit
Use the \(\epsilon \)-\(\delta \) definition of a limit to prove that:
- (a) \(\lim\limits_{x\rightarrow c}A=A\), where \(A\) and \(c\) are real numbers
- (b) \(\lim\limits_{x\rightarrow c}x=c\), where \(c\) is a real number
Solution
(a) \(f(x)=A\) is the constant function whose graph is a horizontal line. Given any \(\epsilon >0\), we must find \(\delta >0\) so that whenever \(0 \lt \vert x-c\vert \lt \delta ,\) then \(\left\vert f(x)-A\right\vert \lt \epsilon \).
Since \(\left\vert A-A\right\vert =0,\) then \(\left\vert f(x)-A\right\vert \lt \epsilon \) no matter what positive number \(\delta \) is used. That is, any choice of \(\delta \) guarantees that whenever \(0 \lt \vert x-c\vert \lt \delta \), then \(\left\vert f(x)-A\right\vert \lt \epsilon \).
(b) \(f( x) =x\) is the identity function. Given any \( \epsilon >0\), we must find \(\delta \) so that whenever \( 0 \lt \vert x-c\vert \lt \delta \), then \(\vert f(x)-c \vert =\vert x-c\vert \lt \epsilon \). The easiest choice is to make \(\delta =\epsilon \). That is, whenever \(0 \lt \vert x-c\vert \lt \delta =\epsilon \), then \(\vert f(x)-c \vert \hspace{-6.5pt}\underset{\underset{\color{#0066A7}{\scriptsize\hbox{f(x) = x}}}{\color{#0066A7}{\uparrow}}}{=}\hspace{-6.5pt} \vert x-c\vert \lt \epsilon \).
Some observations about the \(\epsilon \)-\(\delta \) definition of a limit are given below:
- The limit of a function in no way depends on the value of the function at \(c\).
- In general, the size of \(\delta \) depends on the size of \(\epsilon\).
- For any \(\epsilon \), if a suitable \(\delta \) has been found, any smaller positive number will also work for \(\delta \). That is, \(\delta \) is not uniquely determined when \(\epsilon \) is given.
EXAMPLE 3Using the \(\epsilon \)-\(\delta \) Definition of a Limit
Prove: \(\lim\limits_{x\rightarrow 2}x^{2}=4\).
Solution Given any \(\epsilon >0\), we must show there is a number \(\delta >0\) so that \begin{equation*} \hbox{whenever }\quad 0 \lt \vert x-2\vert \lt \delta \qquad \hbox{ then } \vert x^{2}-4\vert \lt \epsilon \end{equation*}
To establish a connection between \(\vert x^{2}-4\vert \) and \( \vert x-2\vert \), we write \(\left\vert x^{2}-4\right\vert \) as \begin{equation*} \left\vert x^{2}-4\right\vert =\left\vert \,(x+2)(x-2)\right\vert =\left\vert x+2\right\vert \cdot \vert x-2\vert \end{equation*}
Now, if we can find a number \(K\) for which \(\left\vert x+2\right\vert \lt K\), then we can choose \(\delta =\dfrac{\epsilon }{K}\). To find \(K\), we restrict \( x\) to some interval centered at \(2\). For example, suppose the distance between \(x\) and \(2\) is less than \(1\). Then \begin{equation*} \begin{array}{rcl@{\qquad}l} \\[-5pc] &&\vert x-2\vert \lt 1 & \\[3pt] -1&\lt&x-2 \lt 1 & \\[3pt] 1&\lt&x \lt 3 & {\color{#0066A7}{\hbox{Simplify.}}} \\ 1+2&\lt&x+2 \lt 3+2 & {\color{#0066A7}{\hbox{Add 2 to each part. }}} \\ 3&\lt&x+2 \lt 5 & \end{array} \end{equation*}
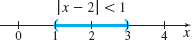
134
In particular, we have \(\vert x+2\vert \lt 5\). It follows that whenever \(\vert x-2\vert \lt 1\), \begin{equation*} \vert x^{2}-4\vert =\left\vert x+2\right\vert \cdot \vert x-2\vert \lt 5\,\vert x-2\vert \hbox{ } \end{equation*}
If \(\vert x-2\vert \lt \delta =\dfrac{\epsilon }{5}\), then \( \left\vert \hbox{ }x^{2}-4\right\vert \lt 5\,\vert x-2\vert \lt 5\cdot \dfrac{\epsilon }{5}=\epsilon \), as desired.
But before choosing \(\delta =\dfrac{\epsilon }{5}\), we must remember that there are two constraints on \(\vert x-2\vert \). Namely, \begin{equation*} \vert x-2\vert \lt 1\qquad \hbox{and}\qquad \vert x-2\vert \lt \dfrac{\epsilon }{5} \end{equation*}
To ensure that both inequalities are satisfied, we select \(\delta \) to be the smaller of the numbers 1 and \(\dfrac{\epsilon }{5}\), abbreviated as \( \delta =\min \left\{ 1,\dfrac{\epsilon }{5}\right\} \). Now, \[ \hbox{whenever } \vert x-2\vert \lt \delta =\min \left\{ 1,\dfrac{\epsilon }{5}\right\} \hbox{ then } \vert x^{2}-4\vert \lt \epsilon \]
proving \(\lim\limits_{x\rightarrow 2}x^{2}=4\).
NOW WORK
In Example 3, the decision to restrict \(x\) so that \(\vert x-2\vert \lt 1\) was completely arbitrary. However, since we are looking for \(x\) close to \(2\), the interval chosen should be small. In Problem 40, you are asked to verify that if we had restricted \(x\) so that \(\vert x-2\vert \lt \dfrac{1}{3}\), then the choice for \(\delta \) would be less than or equal to the smaller of \(\dfrac{1}{3}\) and \(\dfrac{3\epsilon }{13} \); that is, \(\delta \leq \min \left\{ \dfrac{1}{3},\dfrac{3\epsilon }{13} \right\} \).
EXAMPLE 4Using the \(\epsilon \)-\(\delta \) Definition of a Limit
Prove \(\lim\limits_{x\rightarrow c}\dfrac{1}{x}=\dfrac{1}{c}\), where \(c\gt0\).
Solution The domain of \(f(x)=\dfrac{1}{x}\) is \(\{x|x\neq 0\} \).
For any \(\epsilon \gt0\), we need to find a positive number \(\delta \) so that whenever \(0 \lt \vert x-c\vert \lt \delta \), then \(\left\vert \dfrac{1}{x}-\dfrac{1}{c}\right\vert \lt \epsilon \). For \(x\neq 0\), and \(c\gt0\), we have \begin{equation*} \left\vert \frac{1}{x}-\frac{1}{c}\right\vert =\left\vert \frac{c-x}{xc} \right\vert =\frac{\vert c-x\vert }{\vert x\vert \cdot \vert c\vert }=\dfrac{|x-c|}{c\vert x\vert} \end{equation*}
The idea is to find a connection between \begin{equation*} \vert x-c\vert\qquad \hbox{ and }\qquad \dfrac{|x-c|}{c\vert x\vert } \end{equation*}
We proceed as in Example 3. Since we are interested in \(x\) near \(c\), we restrict \(x\) to a small interval around \(c\), say, \(\vert x-c\vert \lt \dfrac{c}{2}\). Then, \begin{equation*} \begin{array}{rcl@{\qquad}l} -\dfrac{c}{2}&\lt&x-c \lt \dfrac{c}{2}\\ \dfrac{c}{2}&\lt&x \lt \dfrac{3c}{2} & {\color{#0066A7}{\hbox{Add \(c\) to each expression.}}} \end{array} \end{equation*}
Since \(c \gt 0,\) then \(x\gt\dfrac{c}{2}\gt0,\) and \(\dfrac{1}{x} \lt \dfrac{2}{c}\). Now \begin{equation*} \left\vert \dfrac{1}{x}-\dfrac{1}{c}\right\vert =\dfrac{|x-c|}{c|x|} \lt \dfrac{2 }{c^{2}}\cdot |x-c|\qquad {\color{#0066A7}{\hbox{Substitute \(\dfrac{1}{\vert x\vert } \lt \dfrac{2}{c}\).}}} \end{equation*}
135
We can make \(\left\vert \dfrac{1}{x}-\dfrac{1}{c}\right\vert \lt\epsilon \) by choosing \(\delta =\dfrac{c^{2}}{2}\epsilon .\) Then \begin{equation*} \hbox{whenever }\vert x-c\vert \lt\delta =\dfrac{c^{2}}{2} \epsilon ,\hbox{ we have }\left\vert \dfrac{1}{x}-\dfrac{1}{c} \right\vert \lt \dfrac{2}{c^2} \cdot |x-c| \lt \dfrac{2}{c^2}\cdot \left(\dfrac{c^2}{2}\cdot \epsilon\right)=\epsilon \end{equation*}
But remember, there are two restrictions on \(|x-c|\). \begin{equation*} \vert x-c\vert \lt\dfrac{c}{2}\qquad \hbox{ and }\qquad \vert x-c\vert \lt\dfrac{c^{2}}{2}\cdot \epsilon \end{equation*}
So, given any \(\epsilon \gt0\), we choose \(\delta =\min \! \left(\! \dfrac{c}{2},\dfrac{c^{2}}{2}\cdot \epsilon\!\! \right) \). Then whenever \(0\lt\vert x-c\vert \lt\delta \), we have \(\left\vert \dfrac{1}{x}-\dfrac{1}{c} \right\vert \lt\epsilon .\) This proves \(\lim\limits_{x\rightarrow c}\dfrac{1 }{x}=\dfrac{1}{c},\) \(c\gt0\).
NOW WORK
The \(\epsilon \)-\(\delta \) definition of a limit can be used to show that a limit does not exist, or that a mistake has been made in finding a limit. Example 5 illustrates how the \(\epsilon \)-\(\delta \) definition of a limit is used to discover a mistake in a computed limit.
EXAMPLE 5Using the \(\epsilon \)-\(\delta \) Definition of a Limit
Use the \(\epsilon \)-\(\delta \) definition of a limit to prove the statement \(\lim\limits_{x\rightarrow 3}(4x-5)\neq 10\).
Solution We use a proof by contradiction.* Assume \( \lim\limits_{x\rightarrow 3}(4x-5)=10\) and choose \(\epsilon =1\). (Any smaller positive number \(\epsilon \) will also work.) Then there is a number \(\delta >0\), so that \begin{equation*} \hbox{whenever }\quad 0\lt\vert x-3\vert \lt\delta\qquad \hbox{then}\quad \vert ( 4x-5) -10\vert \lt1\ \end{equation*}
We simplify the right inequality. \begin{equation*} \begin{array}{rcl} \vert (4x-5)-10 \vert &=& \vert 4x-15 \vert \lt1 \\[3pt] -1&\lt&4x-15\lt 1 \\[3pt] 14&\lt&4x\lt 16 \\[3pt] 3.5&\lt&x\lt 4 \end{array} \end{equation*}
*In a proof by contradiction, we assume that the conclusion is not true and then show this leads to a contradiction.
NOTE
For example, if \(\delta =\dfrac{1}{4}\), then \[ 3-\dfrac{1}{4}\lt x\lt 3+\dfrac{1}{4}\\ 2.75\lt x\lt 3.25 \] contradicting \({3.5\lt x \lt4}.\)
According to our assumption, whenever \(0\lt\left\vert x-3\right\vert \lt\delta ,\) then \(3.5\lt x\lt 4\). Regardless of the value of \(\delta\), the inequality \( 0\lt \left\vert x-3\right\vert \lt \delta \) is satisfied by a number \(x\) that is less than \(3\). This contradicts the fact that \(3.5\lt x\lt 4\). The contradiction means that \(\lim\limits_{x\rightarrow 3}(4x-5)\neq 10.\)
NOW WORK
The next example uses the \(\epsilon \)-\(\delta \) definition of a limit to show that a limit does not exist.
EXAMPLE 6Using the \(\epsilon \)-\(\delta \) Definition of a Limit
The Dirichlet function is defined by \(f(x)=\left\{ \begin{array}{l@{\quad}l} 1 & \hbox{if }x \hbox{ is rational} \\[3pt] 0 & \hbox{if }x \hbox{ is irrational} \end{array} \right. .\)
Prove \(\lim\limits_{x\rightarrow c}\) \(f( x) \) does not exist for any \(c.\)
Solution We use a proof by contradiction. That is, we assume that \(\lim\limits_{x\rightarrow c} f(x)\) exists and show that this leads to a contradiction.
136
Assume \(\lim\limits_{x\rightarrow c}f(x)=L\) for some number \(c\). Now if we are given \(\epsilon =\dfrac{1}{2}\) (or any smaller positive number), then there is a positive number \(\delta \), so that \begin{equation*} \hbox{whenever }\quad 0\lt\vert x-c\vert \lt\delta\qquad \hbox{ then }\quad \vert f( x) -L \vert \lt\dfrac{1}{2} \end{equation*}
Suppose \(x_{1}\) is a rational number satisfying \(0\lt \vert x_{1}-c\vert \lt\delta \), and \(x_{2}\) is an irrational number satisfying \(0\lt\vert x_{2}-c \vert \lt\delta \). Then from the definition of the function \(f\), \begin{equation*} f (x_{1}) =1\qquad \hbox{and}\qquad f( x_{2}) =0 \end{equation*}
Using these values in the inequality \(\vert f(x)-L\vert \lt\epsilon \), we get \begin{equation*} \begin{array}[t]{rcl} \vert f(x_{1})-L\vert &=&\vert 1-L\vert \lt\dfrac{1}{2}\\[5pt] -\dfrac{1}{2}&\lt&1-L\lt\dfrac{1}{2} \\[5pt] -\dfrac{3}{2}&\lt&-L\lt-\dfrac{1}{2} \\[5pt] \dfrac{1}{2}&\lt&L\lt\dfrac{3}{2} \end{array} \quad \hbox{ and }\quad \begin{array}[t]{rcl} \vert f(x_{2})-L\vert &=& \vert 0-L\vert \lt\dfrac{1}{2} \\[5pt] -\dfrac{1}{2}&\lt&-L\lt\dfrac{1}{2} \\[5pt] \dfrac{1}{2}&\gt&L\gt-\dfrac{1}{2} \\[5pt] -\dfrac{1}{2}&\lt&L\lt\dfrac{1}{2} \end{array} \end{equation*}
From the left inequality, we have \(L\gt\dfrac{1}{2}\), and from the right inequality, we have \(L\lt\dfrac{1}{2}\). Since it is impossible for both inequalities to be satisfied, we conclude that \(\lim\limits_{x\rightarrow c}f(x)\) does not exist.
EXAMPLE 7Using the \(\epsilon \)-\(\delta \) Definition of a Limit
Prove that if \(\lim\limits_{x\rightarrow c}f(x)\gt0\), then there is an open interval around \(c\), for which \(f(x)\gt0\) everywhere in the interval except possibly at \(c\).
Solution Suppose \(\lim\limits_{x\rightarrow c}f(x)=L\gt0\). Then given any \(\epsilon \gt0\), there is a \(\delta \gt0\) so that \begin{equation*} \hbox{whenever }\quad 0\lt\vert x-c\vert \lt\delta \qquad \hbox{ then}\quad \vert f(x)-L\vert \lt\epsilon \ \end{equation*}
If \(\epsilon =\dfrac{L}{2}\), then from the definition of limit, there is a \(\delta \gt0\) so that \begin{equation*} \hbox{whenever } 0\lt\vert x-c\vert \lt\delta\quad \hbox{ then } \vert f(x)-L\vert \lt\dfrac{L}{2}\quad \hbox{ or equivalently, } \dfrac{L}{2}\lt f(x)\lt\dfrac{3L}{2} \end{equation*} Since \(\dfrac{L}{2}\gt0\), the last statement proves our assertion that \(f(x)\gt0\) for all \(x\) in the interval \((c-\delta ,c+\delta)\).
In Problem 43, you are asked to prove the theorem stating that if \(\lim\limits_{x\rightarrow c}f(x)\lt0\), then there is an open interval around \(c\), for which \(f(x)\lt0\) everywhere in the interval, except possibly at \(c\).
We close this section with the \(\epsilon \)-\(\delta \) definitions of limits at infinity and infinite limits.
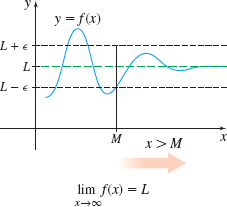
DEFINITION Limit at Infinity
Let \(f\) be a function defined on an open interval \((b,\infty )\). Then \(f\) has a limit at infinity \begin{equation*} \lim_{x\rightarrow \infty }f(x)=L \end{equation*}
where \(L\) is a real number, if given any \(\epsilon \gt 0\), there is a positive number \(M\) so that whenever \(x \gt M\), then \(\vert f(x)-L\vert \lt \epsilon\).
If \(f\) is a function defined on an open interval \((-\infty , a)\), then \begin{equation*} \lim\limits_{x\rightarrow -\infty }f(x)=L \end{equation*}
if given any \(\epsilon \gt 0\), there is a negative number \(N\) so that whenever \(x \lt N\), then \(\vert f(x)-L\vert \lt \epsilon \).
137
Figures 67 and 68 illustrate limits at infinity.

DEFINITION Infinite Limit
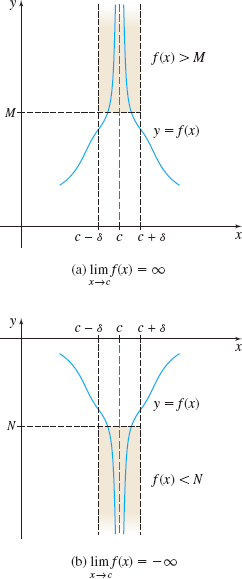
Let \(f\) be a function defined everywhere on an open interval containing \(c\), except possibly at \(c\). Then \(f(x)\) becomes unbounded in the positive direction (has an infinite limit) as \(x\) approaches \(c\), written \begin{equation*} \lim_{x\rightarrow c}f(x)=\infty \end{equation*}
if, for every positive number \(M\), a positive number \(\delta \) exists so that \[ \hbox{whenever } 0\lt\vert x-c\vert \lt \delta \hbox{ then } f(x) \gt M. \]
Similarly, \(f(x)\) becomes unbounded in the negative direction (has an infinite limit) as \(x\) approaches \(c\), written \begin{equation*} \lim\limits_{x\rightarrow c}f(x)=-\infty \end{equation*}
if, for every negative number \(N\), a positive number \(\delta \) exists so that \[ \hbox{whenever } 0\lt\vert x-c\vert \lt \delta \hbox{ then } f(x) \lt N. \]
Figure 69 illustrates infinite limits.
DEFINITION Infinite Limit at Infinity
Let \(f\) be a function defined on an open interval \((b,\,\infty )\). Then \(f\) has an infinite limit at infinity \begin{equation*} \lim_{x\rightarrow \infty }f(x)=\infty \end{equation*}
if for any positive number \(M\), there is a corresponding positive number \(N\) so that whenever \(x \gt N\), then \(f(x) \gt M.\)
A similar definition applies for infinite limits at negative infinity.