5.1 Assess Your Understanding

Printed Page 350

Concepts and Vocabulary

  1. Explain how rectangles can be used to approximate the area enclosed by the graph of a function \(y=f(x) \geq 0,\) the \(x\)-axis, and the lines \(x=a\) and \(x=b.\)

Answers will vary.

  1. True or False  When a closed interval \([a,b] \) is partitioned into \(n\) subintervals each of the same length, the length of each subinterval is \(\dfrac{a+b}{n}\).

False

  1. If the closed interval \([-2,4]\) is partitioned into \(12\) subintervals, each of the same length, then the length of each subinterval is ______.

\(\dfrac{1}{2}\)

  1. True or False  If the area \(A\) under the graph of a function \(f\) that is continuous and nonnegative on a closed interval \([a,b] \) is approximated using upper sums \(S_{n}\), then \(S_{n}\geq A\) and \(A=\lim\limits_{n\rightarrow \infty }S_{n}.\)

True

351

Skill Building

  1. Approximate the area \(A\) enclosed by the graph of \(f(x) = \dfrac{1}{2}x+3,\) the \(x\)-axis, and the lines \(x=2\) and \(x=4\) by partitioning the closed interval \([2, 4] \) into four subintervals: \[ \left[ 2, \dfrac{5}{2}\right], \left[ \dfrac{5}{2},3\right], \left[3, \dfrac{7}{2}\right], \left[ \dfrac{7}{2}, 4\right]. \]

    1. (a) Using the left endpoint of each subinterval, draw four small rectangles that lie below the graph of \(f\) and sum the areas of the four rectangles.
    2. (b) Using the right endpoint of each subinterval, draw four small rectangles that lie above the graph of \(f\) and sum the areas of the four rectangles.
    3. (c) Compare the answers from parts (a) and (b) to the exact area \(A=9 \) and to the estimates obtained in Example 1.

  1. (a) Area is \(\dfrac{35}{4}\).
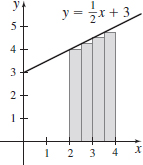
  2. (b) Area is \(\dfrac{37}{4}\).
  3. (c) \(\dfrac{35}{4}<9<\dfrac{37}{4}\)

  1. Approximate the area \(A\) enclosed by the graph of \(f(x) =6-2x,\) the \(x\)-axis, and the lines \(x=1\) and \(x=3\) by partitioning the closed interval \([ 1,3] \) into four subintervals: \[ \left[1, \dfrac{3}{2}\right], \left[ \dfrac{3}{2},2\right], \left[ 2,\dfrac{5}{2}\right], \left[ \dfrac{5}{2},3\right]. \]

    1. (a) Using the right endpoint of each subinterval, draw four small rectangles that lie below the graph of \(f\) and sum the areas of the four rectangles.
    2. (b) Using the left endpoint of each subinterval, draw four small rectangles that lie above the graph of \(f\) and sum the areas of the four rectangles.
    3. (c) Compare the answers from parts (a) and (b) to the exact area \(A=4.\)

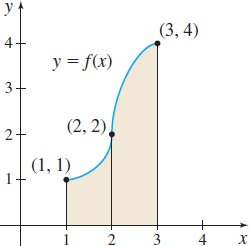
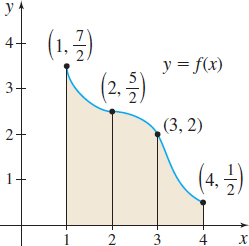
In Problems 7 and 8, refer to the graphs below. Approximate the shaded area under the graph of \(f\):

  1. (a) By constructing rectangles using the left endpoint of each subinterval.
  2. (b) By constructing rectangles using the right endpoint of each subinterval.

  1. (a) \(3\)
  2. (b) \(6\)

In Problems 9–12, partition each interval into \(n\) subintervals each of the same length.

  1. \([1,4]\) with \(n = 3\)

\([1,2], [2,3]\), \([3,4]\)

  1. \([0,9]\) with \(n = 9 \)

  1. \([{-}1,4]\) with \(n = 10 \)

\(\left[-1,-\dfrac{1}{2}\right]\), \(\left[-\dfrac{1}{2},0\right]\), \(\left[0,\dfrac{1}{2}\right]\), \(\left[\dfrac{1}{2},1\right]\), \(\left[1,\dfrac{3}{2}\right]\), \(\left[\dfrac{3}{2},2\right]\), \(\left[2,\dfrac{5}{2}\right]\), \(\left[\dfrac{5}{2},3\right]\), \(\left[3,\dfrac{7}{2}\right]\), \(\left[\dfrac{7}{2},4\right]\)

  1. \([{-}4,4]\) with \(n = 16\)

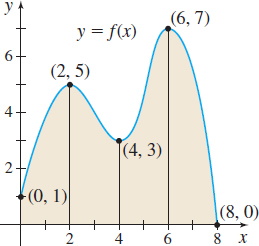
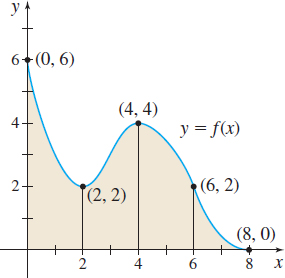
In Problems 13 and 14, refer to the graphs. Approximate the shaded area:

  1. (a) By using lower sums \(s_{n}\) (rectangles that lie below the graph of \(f\)).
  2. (b) By using upper sums \(S_{n}\) (rectangles that lie above the graph of \(f\)).

  1. (a) 14
  2. (b) 48

  1. Area Under a Graph  Consider the area under the graph of \(y=x\) from \(0\) to \(3\).

    1. (a) Sketch the graph and the area under the graph.
    2. (b) Partition the interval \([0,3]\) into \(n\) subintervals each of equal length.
    3. (c) Show that \(s_{n}=\sum\limits_{i=1}^{n}(i-1)\left(\dfrac{3}{n}\right)^{2}\).
    4. (d) Show that \(S_{n}=\sum\limits_{i=1}^{n}{i\left(\dfrac{3}{n}\right)}^{2}\).
    5. (e) Show that \(\lim\limits_{n\rightarrow \infty}s_{n}=\lim\limits_{n\rightarrow \infty } S_{n}={\dfrac{{9}}{{2}}}\).

  1. (a)
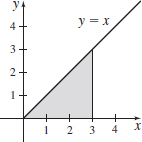
  2. (b) \(\left[0,\dfrac{3}{n}\right]\), \(\left[\dfrac{3}{n},2\cdot\dfrac{3}{n}\right],\ldots, \left[(n-1)\cdot\dfrac{3}{n},3\right]\)
  3. (c) See Student Solutions Manual.
  4. (d) See Student Solutions Manual.
  5. (e) See Student Solutions Manual.

  1. Area Under a Graph  Consider the area under the graph of \(y=4x\) from \(0\) to \(5\).

    1. (a) Sketch the graph and the corresponding area.
    2. (b) Partition the interval \([0,5]\) into \(n\) subintervals each of equal length.
    3. (c) Show that \(s_{n}=\sum\limits_{i=1}^{n}(i-1){\dfrac{100}{n^{2}}}\).
    4. (d) Show that \(S_{n}=\sum\limits_{i=1}^{n} i{\dfrac{100}{n^{2}}}\).
    5. (e) Show that \(\lim\limits_{n\rightarrow \infty} s_{n}={\lim\limits_{n\rightarrow \infty }}S_{n}=50.\)

In Problems 17–22, approximate the area \(A\) under the graph of each function \(f\) from \(a\) to \(b\) for \(n = 4\) and \(n = 8\) subintervals:

  1. (a) By using lower sums \(s_{n}\) (rectangles that lie below the graph of \(f\)).
  2. (b) By using upper sums \(S_{n}\) (rectangles that lie above the graph of \(f\)).

  1. \(f(x) = -x+10\) on \([0,8]\)

  1. (a) \(s_4=40\), \(s_8=44\)
  2. (b) \(S_4=56\), \(S_8=52\)

  1. \(f(x) = 2x + 5\) on \([2, 6]\)

  1. \(f(x) = 16-x^{2}\) on \([0,4]\)

  1. (a) \(s_4=34\), \(s_8=\dfrac{77}{2}\)
  2. (b) \(S_4=50\), \(S_8=\dfrac{93}{2}\)

  1. \(f(x) = x^{3}\) on \([0,8]\)

352

  1. \(f(x) = \cos x\) on \(\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right] \)

  1. (a) \(s_4=\dfrac{\sqrt{2}}{4}\pi\approx 1.111\), \(s_8\approx 1.582\)
  2. (b) \(S_4=\dfrac{\sqrt{2}+2}{4}\pi\approx 2.682\), \(S_8\approx 2.367\)

  1. \(f(x) = \sin x\) on \([0,\pi]\)

  1. Rework Example 3 by using lower sums \(s_{n}\) (rectangles that lie below the graph of \(f\)).

\(s_n=\sum\limits_{i=1}^n \left(3(i-1)\dfrac{10}{n}\right)\dfrac{10}{n}=150-\dfrac{150}{n}\); \(\lim\limits_{n\to \infty} s_n=150\)

  1. Rework Example 4 by using upper sums \(S_{n}\) (rectangles that lie above the graph of \(f\)).

In Problems 25–32, find the area \(A\) under the graph of \(f\) from \(a\) to \(b\):

  1. (a) By using lower sums \(s_{n}\) (rectangles that lie below the graph of \(f\)).
  2. (b) By using upper sums \(S_{n}\)(rectangles that lie above the graph of \(f\)).
  3. (c) Compare the work required in (a) and (b). Which is easier? Could you have predicted this?

  1. \(f(x) =2x+1\) from \(a = 0\) to \(b = 4 \)

  1. (a) \( A = \lim\limits_{n\to \infty} s_n =\lim\limits_{n\to \infty} \left(20- \dfrac{16}{n}\right)=20\)
  2. (b) \( A = \lim\limits_{n\to \infty} S_n =\lim\limits_{n\to \infty} \left(20 + \dfrac{16}{n}\right)=20\)
  3. (c) Answers will vary.

  1. \(f(x) = 3x+1\) from \(a=0\) to \(b=4\)

  1. \(f(x) =12-3x\) from \(a = 0\) to \(b = 4\)

  1. (a) \(A = \lim\limits_{n\to \infty} s_n =\lim\limits_{n\to \infty} \left(24-\dfrac{24}{n}\right)=24\)
  2. (b) \(A = \lim\limits_{n\to \infty} S_n =\lim\limits_{n\to \infty} \left(24 + \dfrac{24}{n}\right)=24\)
  3. (c) Answers will vary.

  1. \(f(x) =5-x\) from \(a = 0\) to \(b=4\)

  1. \(f(x) = 4 x^{2}\) from \(a = 0\) to \(b = 2\)

  1. (a) \(A = \lim\limits_{n\to \infty} s_n =\lim\limits_{n\to \infty} \left(\dfrac{32}{3}-\dfrac{16}{n}+\dfrac{16}{3n^2}\right)=\dfrac{32}{3}\)
  2. (b) \(A = \lim\limits_{n\to \infty} S_n =\lim\limits_{n\to \infty} \left(\dfrac{32}{3}+\dfrac{16}{n}+\dfrac{16}{3n^2}\right)=\dfrac{32}{3}\)
  3. (c) Answers will vary.

  1. \(f(x) = \dfrac{1}{2}x^{2}\) from \(a = 0\) to \(b=3\)

  1. \(f(x) = 4 - x^{2}\) from \(a = 0\) to \(b = 2\)

  1. (a) \(A = \lim\limits_{n\to \infty} s_n =\lim\limits_{n\to \infty} \left(\dfrac{16}{3}-\dfrac{4}{n}-\dfrac{4}{3n^2}\right)=\dfrac{16}{3}\)
  2. (b) \(A = \lim\limits_{n\to \infty} S_n =\lim\limits_{n\to \infty} \left(\dfrac{16}{3}+\dfrac{4}{n}-\dfrac{4}{3n^2}\right)=\dfrac{16}{3}\)
  3. (c) Answers will vary.

  1. \(f(x) = 12-x^{2}\) from \(a = 0\) to \(b = 3\)

Applications and Extensions

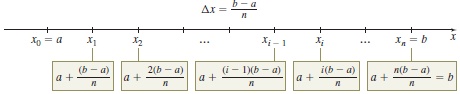
In Problems 33–38, find the area under the graph of \(f\) from \(a\) to \(b.\) [Hint: Partition the closed interval \([a,b]\) into \(n\) subintervals \([x_{0},x_{1}],[x_{1},x_{2}],\) \(\ldots ,\) \([x_{i-1},x_{i}],\) \(\ldots , [x_{n-1},x_{n}],\) where \(a=x_{0}\lt x_{1}\lt\cdots \lt x_{i}\lt\cdots \lt x_{n-1}\lt x_{n}=b,\) and each subinterval is of length \(\Delta x=\dfrac{b-a}{n}.\) As the figure below illustrates, the endpoints of each subinterval, written in terms of \(n\), are \[ \begin{eqnarray*} x_{0} &=& a, x_{1}=a+\dfrac{b-a}{n},\enspace x_{2}=a+2\left(\dfrac{b-a}{n}\right), \ldots , \\ x_{i-1} &=& a+(i-1) \left(\dfrac{b-a}{n} \right),\enspace x_{i}=a+i\left(\dfrac{b-a}{n}\right), \ldots ,\\ x_{n} &=& a+n \left(\dfrac{b-a}{n}\right) \end{eqnarray*} \]

  1. \(f(x)=x+3\) from \(a = 1\) to \(b=3\)

\(10\)

  1. \(f(x)=3-x\) from \(a=1\) to \(b=3\)

  1. \(f(x)=2x+5\) from \(a=-1\) to \(b=2\)

\(18\)

  1. \(f(x)=2-3x\) from \(a=-2\) to \(b=0\)

  1. \(f(x) = 2x^{2}+1\) from \(a = 1\) to \(b = 3\)

\(\dfrac{58}{3}\)

  1. \(f(x) = 4-x^{2}\) from \(a = 1\) to \(b = 2\)

In Problems 39–42, approximate the area \(A\) under the graph of each function \(f\) by partitioning \([a,b]\) into \(20\) subintervals of equal length and using an upper sum.

  1. \(f(x)=xe^{x}\) on \([0,8]\)

\(A\approx 25{,}994\)

  1. \(f(x)=\ln x\) on \([1,3] \)

  1. \(f(x)=\dfrac{1}{x}\) on \([1,5]\)

\(A\approx 1.693\)

  1. \(f(x)=\dfrac{1}{x^{2}}\) on \([2,6]\)

    1. (a) Graph \(y=\dfrac{4}{x}\) from \(x=1\) to \(x=4\) and shade the area under its graph.
    2. (b) Partition the interval \([1,4] \) into \(n\) subintervals of equal length.
    3. (c) Show that the lower sum \(s_{n}\) is \(s_{n}=\sum\limits_{i=1}^{n}\dfrac{4}{\left( 1+\dfrac{3i}{n}\right) }\left(\dfrac{3}{n}\right).\)
    4. (d) Show that the upper sum \(S_{n}\) is \[ S_{n}=\sum\limits_{i=1}^{n}\frac{4 }{\left( 1+\frac{3(i-1) }{n}\right) }\left( \frac{3}{n} \right) \]
    5. (e) Complete the following table:
      \(n\) \(5\) \(10\) \(50\) \(100\)
      \(s_{n}\)
      \(S_{n}\)
    6. (f) Use the table to give an upper and lower bound for the area.

  1. (a)
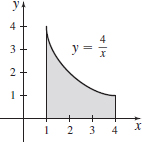
  2. (b) \(\left[1,1+\dfrac{3}{n}\right],\left[1+\dfrac{3}{n},1+2\cdot\dfrac{3}{n}\right],\ldots, \left[1+(n-1)\cdot\dfrac{3}{n},4\right]\).
  3. (c) See Student Solutions Manual.
  4. (d) See Student Solutions Manual.
  5. (e)
    \(n\) \(5\) \(10\) \(50\) \(100\)
    \(s_n\) 4.754 5.123 5.456 5.500
    \(S_n\) 6.554 6.023 5.636 5.590
  6. (f) \(5.500\le A \le 5.590\)

Challenge Problems

  1. Area Under a Graph  Approximate the area under the graph of \(f(x)=x\) from \(a\geq 0\) to \(b\) by using lower sums \(s_{n}\) and upper sums \(S_{n}\) for a partition of \([a,b]\) into \(n\) subintervals, each of length \(\dfrac{b-a}{n}\). Show that \[ s_{n}\lt \frac{b^{2}-a^{2}}{2}\lt S_{n} \]

  1. Area Under a Graph  Approximate the area under the graph of \(f(x)=x^{2}\) from \(a\geq 0\) to \(b\) by using lower sums \(s_{n}\) and upper sums \(S_{n}\) for a partition of \([a,b]\) into \(n\) subintervals, each of length \(\dfrac{b-a}{n}\). Show that \[ s_{n}\lt \frac{b^{3}-a^{3}}{3}\lt S_{n} \]

See Student Solutions Manual.

  1. Area of a Right Triangle  Use lower sums \(s_{n}\) (rectangles that lie inside the triangle) and upper sums \(S_{n}\) (rectangles that lie outside the triangle) to find the area of a right triangle of height \(H\) and base \(B.\)

  1. Area of a Trapezoid  Use lower sums \(s_{n}\) (rectangles that lie inside the trapezoid) and upper sums \(S_{n}\) (rectangles that lie outside the trapezoid) to find the area of a trapezoid of heights \(H_1\) and \(H_2\) and base \(B\).

See Student Solutions Manual.