6 Probability Distributions

6.6Normal Approximation to the Binomial Probability Distribution

This page includes Statistical Videos

OBJECTIVES By the end of this section, I will be able to …

Use the normal distribution to approximate probabilities of the binomial distribution.

1Using the Normal Distribution to Approximate Probabilities of the Binomial Distribution

Recall from Section 6.2 that a binomial experiment satisfies the following four requirements: (1) Each trial must have two possible outcomes. (2) There is a fixed number of trials, $n$ . (3) The experimental outcomes are independent. (4) The probability of observing a success is the same from trial to trial.

For certain values of $n$ and $p$ , it may be inconvenient to calculate probabilities for the binomial distribution. For example, if we are flipping a fair coin 100 times, so that $n = 100$ and $p = 0.5$ , it may be tedious to calculate $P (X \geq 57)$ , which, in the absence of technology, would involve 44 applications of the binomial probability formula. Fortunately, if the requirements are met, we may use the normal distribution to approximate such probabilities.

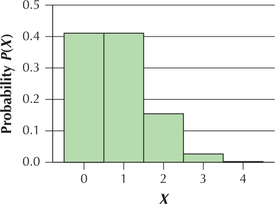
The binomial random variable $X$ represents the number of successes in $n$ trials and thus depends on the sample size $n$ and the probability of success $p$ . For a given probability of success $p$ , if the sample size $n$ gets large enough, the binomial distribution begins to resemble the normal distribution. Figure 71 shows the binomial probability distribution for Example 16 (page 330), where 20% ( $p = 0.2$ ) of Americans are sleep-deprived and we sampled $n = 4$ Americans. The distribution of X = the number of Americans who are sleep-deprived in Figure 71 is clearly not normal.

FIGURE 71 Binomial distribution:

$n = 4$ ,

$p = 0.2$ .

Page 386

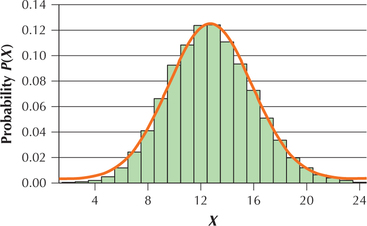
If we increase the sample size to $n = 64$ (Figure 72), the binomial distribution of $X$ for $n = 64$ and $p = 0.2$ , which is discrete, looks like it can be nicely approximated by the normal distribution, which is continuous.

FIGURE 72 Binomial distribution:

$n = 64$ ,

$p = 0.2$ .

We generalize this behavior as follows.

The Normal Approximation to the Binomial Probability Distribution

For the binomial random variable $X$ with probability of success $p$ and number of trials $n$ : if $n \cdot p \geq 5$ and $n \cdot q \geq 5$ , the binomial distribution may be approximated by a normal distribution with mean $μ_{X} = n \cdot p$ and standard deviation $σ_{X} = \sqrt{n \cdot p \cdot q}$ .

These values for $μ_{x}$ and $σ_{x}$ are the same as the values for $μ$ and $σ$ for a binomial random variable that we learned about on page 334.

EXAMPLE 44The normal approximation to the binomial distribution

The Centers for Disease Control and Prevention reported that 20% of preschool chil dren lack required immunizations, thereby putting themselves and their classmates at risk. For a group of $n = 64$ children with $p = 0.2$ , the binomial probability distribution is shown in Figure 72.

Verify that this distribution can be approximated by a normal distribution.
Find the mean and standard deviation of this normal distribution.

Solution

The normal approximation is valid if $n \cdot p \geq 5$ and $n \cdot q \geq 5$ . Substituting $n = 64$ and $p = 0.2$ , we get $\begin{matrix} n \cdot p = (64) (0.2) = 12.8 \geq 5 & and & n \cdot q = (64) (0.8) = 51.2 \geq 5 \end{matrix}$
Thus, the normal approximation is valid.
The mean and standard deviation of the normal distribution are

$\begin{array}{l} μ_{x} = n \cdot p & = & (64) (0.2) = 12.8 \\ σ_{x} & = & \sqrt{n \cdot p \cdot q} & = & \sqrt{(64) (0.2) (0.8) = 3.2} \end{array}$

NOW YOU CAN DO

Exercises 3–8.

Figure 73 reproduces Figure 72, with the rectangle for $X = 12$ highlighted. The height of the rectangle represents the binomial probability that exactly 12 of the 64 children lack the required immunizations, that is, $P$ ( $X = 12$ ). The width of the rectangle equals $12.5 - 11.5 = 1$ , so it follows that the area of the rectangle also represents the binomial probability that $X = 12$ . Now, the area under the normal curve between 11.5 and 12.5 is approximately equal to this rectangle, which is $P (X > X_{12})$ for the binomial random variable $X$ , with $n = 64$ and $p = 0.2$ . That is,

$P (X_{binomial} = 12) \approx P (11.5 \leq Y_{normal} \leq 12.5)$

Page 387

FIGURE 73 Normal curve approximates binomial distribution.

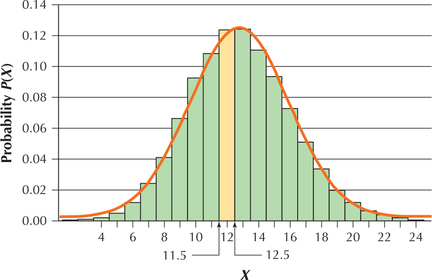
where $Y_{normal}$ is the normal random variable from Example 44(b), with mean $μ_{x} = 12.8$ and standard deviation $σ_{x} = 3.2$ .

The 0.5 that we add and subtract from 12 when approximating the binomial distribution with the normal distribution is called the continuity correction, because it is an adjustment for approximating a discrete probability with a continuous one. When using the normal approximation to the binomial, the analyst must determine which binomial rectangles are included and apply the continuity correction accordingly. This is shown in Table 9, which provides a listing of several types of binomial probabilities and their normal probability approximations.

Table 6.39: Table 9Binomial probabilities and approximate normal probabilities

Exact binomial probability	Approximate normal probability
$P (X_{binomial} = a)$	$P (a - 0.5 \leq Y_{normal} \leq a + 0.5)$
$P (X_{binomial} \leq a)$	$P (Y_{normal} \leq a + 0.5)$
$P (X_{b i n o m i a l} \geq a)$	$P (Y_{normal} \geq a - 0.5)$
$P (X_{b i n o m i a l} < a)$	$P (Y_{normal} < a - 0.5)$
$P (X_{binomial} > a)$	$P (Y_{n o r m a l} > a - 0.5)$
$P (a \leq X_{binomial} \leq b)$	$P (a - 0.5 \leq Y_{n o r m a l} \leq b + 0.5)$
$P (a < X_{binomial} < b)$	$P (a + 0.5 < Y_{normal} < b - 0.5)$

EXAMPLE 45Performing the normal approximation to the binomial probability distribution

For a group of $n = 64$ preschool children with the probability of lack of immunization $p = 0.2$ , perform the following approximations:

Approximate the probability that there are, at most, 12 children without immunizations.
Approximate the probability that there are more than 12 children without immunizations.

Page 388

Solution

Once again, we have a binomial experiment with $n = 64$ and $p = 0.2$ .

“At most” 12 children means 12 or fewer children. That is, $X = 12$ and $X = 11$ and $X = 10$ , and so on; that is, $P (Y_{binomial} \leq 12)$ . In this case, we see that $X = 12$ is included in the probability we seek, as shown in Figure 74. From Table 9, we see that $P (X_{binomial} \leq 12)$ is of the form $P (X_{binomial} \leq a)$ . Thus, our continuity correction takes the form $P (Y_{normal} \leq a + 0.5)$ , where we add 0.5 to 12, so that

$P (X_{binomial} \leq 12) \approx P (Y_{normal} \leq 12.5)$

Recall that $μ_{x} = 12.8$ and $σ_{x} = 3.2$ . We use the TI-83/84, as shown in Figures 75 and 76, and find that the probability that, at most, 12 children lack immunizations is $0.462653813 \approx 0.4627$ .

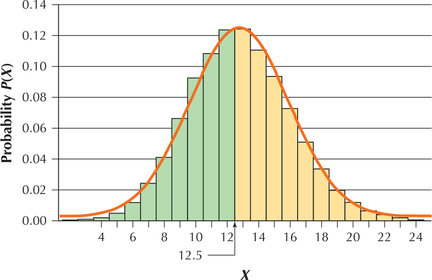FIGURE 74 Approximates a binomial probability with a normal probability.

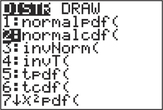FIGURE 75 TI-83/84.

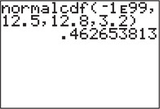FIGURE 76 TI-83/84 results.
“More than” 12 children means $X = 13$ and $X = 14$ , and so on. In other words, $X = 12$ is not included. That is, we want $P (X_{binomial} > 12)$ . From Table 9, we see that $P (X_{binomial} > 12)$ is of the form $P (X_{binomial} > a)$ . Thus, our continuity correction takes the form $P (Y_{normal} > a + 0.5)$ , where we add 0.5 to 12, so that

$P (X_{binomial} > 12) \approx P (Y_{normal} > 12.5)$

The desired area is the complement of the green area in Figure 74, so we can find the answer like this:

$P (X_{binomial} > 12) \approx P (Y_{normal} > 12.5) = 1 - P (Y_{normal} \leq 12.5) = 1 - 0.4627 = 0.5373$

The probability that more than 12 preschool children will not have the required immunizations is 0.5373.

The Normal Approximation to the Binomial Distributions applet allows you to choose your own values of $n$ and $p$ and see how changes in these values affect the normal approximation to the binomial distribution.

NOW YOU CAN DO

Exercises 9–24.

Page 389

YOUR TURN#23

For the scenario in Example 45, approximate the probability that there are less than 12 children without immunizations.

(The solution is shown in Appendix A.)