Chapter 18 Exercises
Chapter 18 Exercises
Most of the exercises require scientific functions calculator.
18.1 Geometric Similarity
Question 18.31
1. Your digital camera probably takes pictures with an aspect ratio of 4 to 3, meaning that the longer side is 4/3 times as long (in pixels) as the shorter side. For example, you probably can take a “small” picture with 640 pixels by 480 pixels, or perhaps a “large” picture with 2592 pixels by 1944 pixels (for a total of 2592×1944 pixels, or just a little more than 5 megapixels). Photographic prints from your digital camera are available in various sizes of paper, quoted in inches: 4×6,5×7, and 8×10.
- Which of the paper sizes, if any, is geometrically similar to the original digital image?
- If a 4×6 print is made by scaling the shorter side of the digital image to be exactly 4 in., how long should the longer side of the image be on the print?
- If a 4×6 print is made by scaling the longer side of the digital image to be exactly 6 in., how long should the shorter side of the image be on the print? (Hint: The paper isn’t wide enough!)
1.
(a) None
(b) 4 in.×43=513 in.
(c) 6 in.×34=412 in.
For Exercises 2–3, refer to the following: The area of a circle of radius r is πr2. Expressed in terms of the diameter, d=2r, the area is πd2/4. If we apply a linear scaling factor L to the diameter, then the area of the scaled circle—just as is the case for a square—changes with L2, the square of the linear scaling factor.
Question 18.32
2. A natural application of this idea is to pizza. The prices at Vince’s pizza restaurant in Beloit, Wisconsin, are $7.57, $8.71, $9.49, $11.13, and $12.63, respectively, for small (10-in.), medium (12-in.), large (14-in.), extra-large (16-in.), and XX-large (18-in.) cheese pizzas.
- What is the linear scaling factor for an XX-large pizza compared with a small one?
- How many times as large in area is the extra-large pizza compared with the small one?
- How much pizza does each size give per dollar? What “hidden” assumptions are you making about how the pizzas are scaled up?
- The corresponding prices for a pizza with six toppings are $12.35, $15.49, $18.42, $21.60, and $25.74. Is there any size of these for which you get more pizza per dollar than some size of the cheese pizzas? (Curiously, all the prices are, to the nearest cent, exactly $0.10 higher than four years earlier! That is an example of arithmetic scaling.)
Question 18.33
3. The NBC Nightly News on June 21, 2010, featured a story about food portions, stating that dinner plates were 9 in. in diameter in the 1960s but now they are 12 in. in diameter, “making room for one-third more food.”
The NBC Nightly News on June 21, 2010, featured a story about food portions, stating that dinner plates were 9 in. in diameter in the 1960s but now they are 12 in. in diameter, “making room for one-third more food.”
- What is the linear scaling factor for a 12-in. plate compared with a 9-in. plate?
- How many times as large in area is a 12-in. plate compared with a 9-in. plate?
- What percentage greater is the area of a 12-in. plate compared with a 9-in. plate?
3.
(a) 113≈1.33
(b) 1.378
(c) 78%
Question 18.34
4. Dollhouses and their furnishings are usually built to a scale of exactly 1 in. to 1 ft, meaning that an item 1 ft long in a real house is 1 in. long in a dollhouse.
- What is the linear scaling factor for a dollhouse?
- If a dollhouse were made of the same materials as a real house, how would their weights compare?
Question 18.35
5. Shellac O’Lean, a freshman on your school’s football team, is 6 ft tall and weighs 150 lb. Since he would rather play basketball, he plans to grow to 7 ft 1 in., the same height as Shaquille O’Neal, his idol. If Shellac scales geometrically as he grows, how much can he expect to weigh? (O’Neal weighs 325 lb.)
5.
247lb
Question 18.36
6. At our house, we have a 10-in. frying pan and a 12-in. frying pan; the 12-in. one weighs a lot more, cooks food more slowly, and never gets as hot. Suppose that a 10-in. frying pan weighs 1 lb, apart from its handle. How much would a geometrically similar 12-in. frying pan weigh? How much would it weigh if it had the same thickness of metal as the 10-in. pan?
Question 18.37
7. The human figures in Lego sets are 4 cm tall (without hats or helmets).
- What is the linear scaling factor of a Lego figure if it represents a human who is 160 cm tall?
- How does the volume of a real human compare with the volume of a Lego figure?
- The car in one Lego set is 10 cm long. Using the linear scaling factor in part (a), how long would a real car be?
7.
(a) 140=0.025
(b) 64,000 times as large
(c) 400 cm=4.00 m=13.1 ft
Question 18.38
8. Recent dollar coins (Presidential, Susan B. Anthony, Sacagawea) have been largely rejected by the public, which finds them too small and too light. Suppose that you are appointed to the U.S. Citizens Coinage Advisory Committee and commissioned to design a new $5 coin. (Whom should it depict?) The sole requirement is that it be made of the same material as the quarter but weigh 4 times as much. A quarter can be described geometrically as a circular cylinder approximately 24.26 mm in diameter and 1.75 mm thick. Because your new dollar should weigh 4 times as much, it needs to have 4 times the volume of a quarter. [The formula for the volume of a cylinder is h(d/2)2, where h is the height and d is the diameter.]
- A member of your public advisory panel suggests just doubling the diameter and doubling the thickness. What do you tell this individual, in the most diplomatic terms?
- If you double the diameter, how thick does the coin need to be?
- Another member feels that the result of part (b) would be inconveniently large and proposes instead to scale up the quarter proportionally. (She studied a previous edition of this book.) What would the dimensions be for this coin?


Question 18.39
9. Criticize the following statement and write a correct version.
Murders by firearms in Britain are 30 times fewer per capita than in the US.
—ragingbull.com/forum/topic/449338
9.
The writer uses both multiplicative and subtractive language together. Better: “ … one-thirtieth as common per capita….”
Question 18.40
10. Criticize the following statement and write a correct version.
Energizer Ultimate Lithium … designed to last up to 9x longer, which means up to 9x less waste.
—Formerly stated on the Energizer website
Question 18.41
11. Criticize the following statement and write a correct version.
Cadmium chloride is a nasty chemical… used as a coating for thin-film solar cells because it increases the efficiency of converting sunlight to energy…. [In tests] magnesium chloride … yielded comparable efficiency…. Magnesium chloride is also nontoxic, abundant and costs about 300 times less than cadmium chloride.
—Scientific American 311(3) (September 2014): 20
11.
The writer uses both multiplicative and subtractive language together. Better: “ … one three-hundredth as much as….”
Question 18.42
12. Criticize the following statement and write a correct version.
Antibiotics for children that are covered by private insurance cost five times more in the United States than in the United Kingdom.
—consumer.healthday.com/public-health-information-30/health-cost-news-348/briefs-emb-12-19-antibiotic-costs-pharmacotherapy-bumc-release-batch-1071-683273.html
Question 18.43
13. Abuses of the language of comparison aren’t hard to find. For example, the phrase “times less than” occurs more than 1 million times in documents on the Internet. Search on the Internet to find an abuse of “times” and “less than” together, figure out what the author meant to say, and write it in correct language.
13.
Answers will vary.
Question 18.44
14. The phrase “times more than” occurs suprisingly more frequently on the Internet than “times less than"— more than 29 million times. Search on the Internet to find an abuse of “times” and “more than” together, figure out what the author meant to say, and write it in correct language.
18.2 How Much Is That in …?
Question 18.45
15. In 1991, Edward N. Lorenz, a meteorologist who was an early researcher into chaos and dynamical systems (discussed in Chapter 23), received the Kyoto Prize in Basic Sciences, consisting of a gold medal and 45 million Japanese yen (¥). If US$1=¥125 at the time, what was the value of the cash award in 1991 U.S. dollars? (In Chapter 21, we show how to convert such an amount to its value in today’s dollars.)
15.
$360,000
For Exercises 16–20, refer to the following. Energy can be thought of as power applied over time. Power can be measured in kilowatts and energy in kilowatt-hours (kWh), where 1 kilowatt-hour is 1000 watts of power exerted for 1 hour. For example, a 40-watt bulb burning for 24 hours consumes 960 watt-hours ≈ 1 kWh. Other forms of energy, such as food or gasoline, can be converted to an equivalent in kWh.
Question 18.46
16. An average adult in the U.S. consumes about 2500 food calories per day; one food calorie has the same energy as 1.16×10−3KWh. A gallon of gasoline contains 33.7 kWh of energy. Compare the energy consumption of a car that gets 30 mpg and is driven about 30 mi/day (say, 12,000 mi/yr) with the food energy consumption of its driver. What do you conclude?
Question 18.47
17. The Toyota Prius recovers energy to its battery when the car brakes. In the “classic” Prius model (2002-2003), for each 50 watt-hours (Wh) of energy recovered, an icon appears on the dashboard screen. A gallon of gasoline contains 33.7 kWh of energy. Suppose gasoline costs $3.00/gal. How many icons would have to appear before the car saves $1 in gasoline cost? (We neglect consideration of the relative efficiency of the car in converting gasoline or recovered electrical energy into mechanical motion.)
17.
225 (So it’s mainly a “feel-good” icon.)
Question 18.48
18. About 435×103 km2 of U.S. land could be devoted to wind energy (“without raising too many hackles,” according to Englishman David J. C. Mackay, Sustainable Energy—Without the Hot Air, UIT Cambridge, 2009, p. 234). The windmills would generate on average 1.2 W/m2. (The hardware required would be 100 times as much as is currently installed.)
- How much is that land area in square miles?
- How much electricity would be produced per year?
- Suppose instead that all that area were covered with solar cells producing electricity at an annual average of 1600 kWh/m2. How much electricity would be produced per year?
- How much energy per day would that amount to per person in the United States, in kWh/d? (The United States has about 315 million people; over all forms of energy usage throughout society—manufacturing, transport, heat, electricity and its production—Americans average the equivalent of 250 kWh/d per person.)
For Exercises 19–20, refer to the following. How can an all-electric car get 99 mpg? The figure below shows the EPS fuel economy label for an all-electric car. The fuel economy is measured in miles per gallon gasoline equivalent (MPGe). A gallon of gasoline equivalent means the amount of alternative fuel (electricity, natural gas, or hydrogen) that contains the same energy as in a gallon of gasoline.

The fuel economy label cites how many kilowatt- hours (kWh) of energy the vehicle uses per 100 miles— namely, 34 kWh. That number in turn is converted to MPGe via the equation
MPGe=kWh content of 1 gallon of gasolinekWh consumed per mile=33.705 kWh/galnumber of kWh/mi=3370.5 kWh/galnumber of kWh/100 mi
Thus, in the label shown, the number of kWh/100 mi is 34, so the MPGe=3,370.5/34≈99mi/gal.
Question 18.49
19. The 2015 Kia Soul Electric vehicle uses a combined city/highway 32 kWh/100 mi.
- What does the electricity cost to drive it 15,000 mi/yr at a cost of $0.12/kWh?
- What is the car’s MPGe?
- The fuel economy labels in Great Britain for electric cars give just the energy consumption in mi/kWh. For example, the 2012 Nissan Leaf is rated at 3.5 mi/kWh. What is the corresponding MPGe?
19.
(a) $576
(b) 105 MPGe
(c) 118 MPGe
Question 18.50
20. Light-duty vehicles (passenger cars and trucks) travel about 2.66 trillion miles per year. Suppose that all of them were converted to run on electric power at 34 kWh/100 mi. How much electricity would be required annually?
Question 18.51
21. In mid-2015, the cost of mailing a letter from the United States to the rest of the world was $1.15. How much was that in euros (€), the currency of the European Union (EU) in mid-2015, when the exchange rate was €1=$1.10? (For comparison, the cost then of a letter to the United States from the EU ranged from €0.51 to €1.70, depending on the country.)
21.
€1.05
Question 18.52
22. The cost of mailing a letter from the United States to Canada in mid-2015 was USD $1.15. How much was that in Canadian dollars when the exchange rate was USD$1=CAD$1.24? (The postage cost from Canada to the United States was CAD $1.10.)
Question 18.53
23. In Germany, the fuel efficiency of cars is measured in liters of fuel per 100km(L/100km). A typical average in a compact station wagon is 7.3L/100km. What is that in miles per gallon (mpg)?
23.
32 mpg
Question 18.54
24. According to EPA ratings, the highest city gas mileage for non-electric 2015 cars was with the hybrid Toyota Prius c, at 53 mpg in the city. How many liters of gasoline does such a Prius use to travel 100 km in the city?
Question 18.55
25. Consider a real locomotive that weighs 88 tons and an HO-gauge scale model of it, for which the linear scaling factor is 1/87.
- How much would an exact scale model weigh in tons?
- What assumptions are involved in your answer to part (a)?
- How much would an exact scale model weigh in pounds?
- How much would an exact scale model weigh in kilograms?
- How much would an exact scale model weigh in tonnes (1 tonne = 1 metric ton = 1000 kg)?
25.
(a) 0.00013364 tons
(b) That all parts of the scale model are made of the same materials as the real locomotive
(c) 0.267 lb
(d) 0.121 kg
(e) 0.000121 metric tonnes
Question 18.56
26. What’s wrong in the following quotations?
President Bush visited California, where 12 forest fires have charred more than 700,000 square miles.
—Steve Stadelman, WTVO television news, Channel 17, Rockford, Illinois, October 2007. (Curiously, exactly the same number, 700,000, also appeared in news reports for California fires in 2014, 2011, 2003, 2000, and 1987.)
The population of the USA has topped 300 million … If current trends continue, it is expected to reach 400 billion by 2043. This makes it an acceleration of growth.
—Significance 3(4) (December 2006): 146
Question 18.57
27. Gasoline is sold in the United States by the U.S. gallon and in Europe by the liter (1 U.S. gal = 231 in.3;1 L = 1000 cm3). What was the equivalent cost, in U.S. dollars per U.S. gallon, for gasoline in Germany priced in euros at €1.59 per liter, when €1=$1.24, in December 2014?
27.
$4.85
Question 18.58
28. Consider which uses more energy: your house— with heating, cooling, electric, and perhaps gas for cooking—or the cars in the household (say, 2). A common measure of energy is 1 BOE, one barrel of oil equivalent, the approximate energy released by burning one barrel of crude oil, for which we have
1BOE≈5800 ft3 natural gas ≈1.7 MWh electricity ≈40 gal gasoline
- Suppose that in 1 year, your household uses 7000 kWh of electricity plus 700 therms of natural gas (1 therm ≈ 100 ft3) for heating, and that the household has two cars that get an average of 25 mpg and are each driven 15,000 miles per year. Which uses more energy: your house or the cars?
- Recalculate your answer to part (a) to take into account that conversion of natural gas, oil, or coal into electricity is at best only 40% efficient, while natural gas for heating can be about 90% efficient.
Question 18.59
29. Before 1933, the United States issued gold coins for general circulation, the highest denomination being $20. (The U.S. mint still produces gold coins but for collecting and investment purposes.) Suppose that you want to make gold coins available again, with the value of the coin the same as the value of the gold in it. Such a coin would be round and have a thickness of 1 mm (that is half the thickness of current $1 coins and thinner than a dime). Gold has a density of 19.3 g/cm3; and the volume of a cylinder is V=πr2h, where r is the radius and h is the height (thickness). At a price of $1200 per ounce, what would be the diameter of a $20 gold coin?
29.
0.28 cm = 2.9 mm. You would barely be able to see it!
18.3 Big Stuff
Question 18.60
30. The weight of a 1-ft cube of steel is 500 lb. What is the pressure on the bottom face in
- pounds per square inch?
- atmospheres (1 atm = 14.7 lb/in.2)?
Question 18.61
31. The express elevators to the observation deck of One World Trade Center in New York City travel a height of 1293 feet in 47 seconds, reaching a speed of 2000 ft/min.
- How much is 2000 ft/min in miles per hour?
- How much is 2000 ft/min in meters per second?
31.
(a) 23 mph
(b) 10 m/s
Question 18.62
32. As is the case for One World Trade Center, elevators in others of the world’s tallest buildings usually take less than 1 minute to get to the top. How fast, in meters per second, would the elevators in a mile-high building have to be to achieve that standard?
Question 18.63
33. At birth, the average human female baby weighs 7 lb and is 19 in. in length (height). At 15 months of age, the average weight is 21 lb. What would you expect the height to be then? (Thanks for the idea to Shai Simonson, Stonehill College.)
33.
Assuming geometric scaling, 3√21/7×19≈27 in.
For Exercises 34 and 35, refer to the following. A mature gorilla weighs 400 lb and stands 5 ft tall; its two feet combined have an area of about 1 ft2.
Question 18.64
34. (a) Give an estimate of the gorilla’s weight when it was half as tall.
(b) What assumptions are involved in your estimate?
(c) When the gorilla is standing, what is the pressure on its feet in pounds per square inch?
Question 18.65
35. Suppose that King Kong is a gorilla scaled up with a linear scaling factor of 10.
- How much does the King weigh?
- What is the pressure on the King’s feet in pounds per square inch?
35.
(a) 400,000 lb
(b) 28 lb/in2.
Question 18.66
36. You may want a waterbed, but waterbeds are not allowed in your building. Apart from the danger of flood if the bed should puncture or leak, the weight is an issue.
- Suppose that a queen-size waterbed mattress is 80 in. long by 60 in. wide by 12 in. high, and water weighs 1kg/L. How much does the water in the mattress weigh in pounds?
- If the weight of the mattress and frame is carried by four legs, each 2 in. by 2 in., what is the pressure, in pounds per square inch, on each leg?
- How does the pressure on the legs of the waterbed compare with the pressure that a person exerts on his or her feet—for example, a 130-lb person with a total foot area of about one-quarter of a square foot in contact with the ground?
Question 18.67
37. If you aren’t allowed to have a waterbed, how about a spa (hot tub)? Find the weight of the water in a spa that is in the shape of a cylinder 6 ft in diameter and 3.5 ft deep. (Hint: The volume of a cylinder is πr2h, where r is the radius and h is the height.)
37.
6200 lb, or 2800 kg
Question 18.68
38. What does the largest giant sequoia tree (named “Hyperion”) weigh? Model the tree as a (very elongated) cone. Assume that the tree is 379 ft high, has a circumference of 40 ft at the base, and that the density of the wood is 31 lb/ft3. (The volume of a cone of height h and radius r is 13r2h.)
Question 18.69
39. A 6-ft-tall indoor holiday tree needs four strings of lights to decorate it. How many strings of lights are needed for an outdoor tree that is 30 ft high? (Thanks for the idea to Charlotte Chell, Carthage College, Kenosha, Wisconsin.)
39.
The lights are strung around the outside of the tree branches, so in effect they cover the outside “area” of the tree (thought of as a cone). Hence, the number of strings needed grows in proportion to the square of the height: a 30-ft tree will need 52 = 25 times as many strings as a 6-ft tree. However, you could also argue that a 30-ft tree is meant to be viewed from farther away, so that stringing the lights farther apart on the 30-ft tree would produce the same effect as with the shorter tree.
For Exercises 40 and 41, refer to the following. An ancient measure of length, the cubit, was the distance from the elbow to the tip of the middle finger of a person’s outstretched arm. So the length of a cubit depended on the person, though there was some attempt at standardization. Most estimates place the cubit between 17 and 22 in.
Question 18.70
40. According to Genesis 6:15, Noah was to build an ark: “The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits.” How does the volume of such an ark compare with that of a U.S. suburban house totaling 2000 ft2, with 8-ft ceilings?
Question 18.71
41. Goliath [of David and Goliath, as related in the Bible (I Samuel 17:4)] was “six cubits and a span.” A “span” was originally the distance from the tip of the thumb to the tip of the little finger when the hand is fully extended, about 9 in. What range of heights would this indicate for Goliath in feet and inches? In centimeters?

41.
9 ft 3 in. to 11 ft 9 in. (in modern times, there have been men over 9 ft tall); 282 cm to 358 cm.
For Exercises 42–44, refer to the following. The body mass index (BMI) is the basis for the National Heart, Lung, and Blood Institute’s weight guidelines. BMI is body weight (in kilograms) divided by the square of height (in meters). A BMI of 25 through 29 is considered “overweight”; a BMI of 30 or over is considered “obese.” Some 55% of American adults have a BMI of 25 or above. (Note: BMI is not a useful measure for young children, pregnant or breastfeeding women, the frail elderly, or very muscular people.) For practice with this concept, calculate your own BMI.
Question 18.72
42. Calculate the BMI for a woman 160 cm tall who weighs 65 kg. Is she overweight according to the institute’s guidelines?
Question 18.73
43. Suppose that weight and height are measured instead in U.S. customary units of pounds and inches. We can still calculate body weight divided by the square of height using these units. What conversion factor is necessary to convert this number to the BMI?
43.
You must multiply the value calculated from pounds and inches by 703.
Question 18.74
44. Calculate the BMI of a man who is 6 ft 2 in. tall and weighs 217 lb.
18.4 Dimension Tension
Question 18.75
45. (a) Refer to Example 10 (page 756). What would you expect an individual Q. northropi to weigh if it had half the wingspan of an adult?
(b) If an individual weighed half as much as an adult, what would you expect its wingspan to be?
45.
Assuming geometric growth:
(a) (12)3=one-eighth as much, or about 12 lb
(b) 123 as much, or about 29 ft
Question 18.76
46. In the children’s story Peter Pan, Peter and Wendy can fly. We may suppose that they are 4 ft tall, so they are about 8 times as tall as a sparrow is long. What should their minimum flying speed be?
Question 18.77
47. Icarus of Greek legend escaped from Crete with his father, Daedalus, on wings made by Daedalus and attached with wax. Against his father’s advice, Icarus flew too close to the sun; as a result, the wax melted, the wings fell off, and he plunged into the sea and drowned. What must have been his minimum cruising speed? What assumptions does your answer involve?
47.
Sample response: Icarus would have been about as tall as an adult female ostrich; hence, if shaped like an ostrich, he would have had to fly about 100 mph.
Question 18.78
![]() 48. A typical ultralight aircraft (with pilot on board) weighs about 400 lb, has a wingspan of 28 ft, and has a maximum speed of 65 mph. Also, solar and human-powered aircraft, such as the Gossamer Condor and other superlightweight planes, fly more slowly than Example 10 (page 756) predicts; for instance, the Gossamer Condor is far longer than an ostrich, but it flies at only 12 mph. How are these aircraft possible?
48. A typical ultralight aircraft (with pilot on board) weighs about 400 lb, has a wingspan of 28 ft, and has a maximum speed of 65 mph. Also, solar and human-powered aircraft, such as the Gossamer Condor and other superlightweight planes, fly more slowly than Example 10 (page 756) predicts; for instance, the Gossamer Condor is far longer than an ostrich, but it flies at only 12 mph. How are these aircraft possible?
Question 18.79
49. Justify the claim in Example 10 on page 756 that a Q. northropi weighing 200 lb with a wingspan of 50 ft would have had the same wing loading as one weighing 100 lb with a wingspan of 36 ft.
49.
The square of wingspan is proportional to wing area, so the wing loading is proportional to weight divided by square of wingspan. For the 200-pounder, that ratio is 200/(502)=0.080, while for the 100-pounder it is 100/(362)≈0.077—close enough.
Question 18.80
![]() 50. Jonathan Swift’s Gulliver traveled to Lilliput, where the Lilliputians were human-shaped but only about 6 in. tall. In other words, they were geometrically similar in shape to ordinary human beings but only one-twelfth as tall. What would a Lilliputian weigh? Are Lilliputians ruled out by the size-shape and area-volume considerations in this chapter? If you think they are, what considerations do you find convincing? If not, why not?
50. Jonathan Swift’s Gulliver traveled to Lilliput, where the Lilliputians were human-shaped but only about 6 in. tall. In other words, they were geometrically similar in shape to ordinary human beings but only one-twelfth as tall. What would a Lilliputian weigh? Are Lilliputians ruled out by the size-shape and area-volume considerations in this chapter? If you think they are, what considerations do you find convincing? If not, why not?
Question 18.81
51. The cult movie Them (1954) features enormous ants (8 m long by 3 m wide). We can investigate the feasibility of such a scaled-up insect by considering its oxygen consumption. A common ant, 1 cm long, needs 24 milliliters (mL) of oxygen per second for each cubic centimeter of its volume. Because an ant has no lungs, it absorbs oxygen through its “skin” at a rate of 6.2 mL per second per square centimeter. Suppose that the tissues of a scaled-up ant would have the same need for oxygen for each cubic centimeter, and that the ant’s skin could absorb oxygen at the same rate as a common ant.
- Compared with a common ant, how many times as large is an enormous ant’s length, surface area, and volume?
- What proportion of such an ant’s oxygen need could its skin supply?
- What can you conclude about the existence of such insects? (Adapted from George Knill and George Fawcett, Animal form or keeping your cool, Mathematics Teacher, May 1982, 395–397.)
51.
(a) Length = 800; surface area = 640,000; volume = 512,000,000
(b) One eight-hundredth
(c) There couldn’t be any such giant ants.
For Exercises 52–55, refer to the following. Maybe some trees could grow to a mile high, but they just don’t live long enough to have the chance. In this problem, we try to determine how fast the height of a tree increases. We can measure indirectly how much mass the tree adds in a year by the area of the annual tree ring added. Here are two relevant facts:
- As you may have noticed from stumps, as a tree grows older, its annual rings get less wide. Although the width of the ring varies somewhat from year to year with the amount of rainfall and other factors, the total area of each annual ring is roughly the same over the years, meaning that the tree adds roughly the same amount of mass each year. Call that amount a; the mass M of the tree is at, where t is its age in years.
- Over a large range of tree sizes and tree species, the diameter d of a tree of a species is approximately proportional to the three-halves power of the height h of the tree. (Different species have different constants of proportionality.) Thus, d∝h3/2 (which is shown in Exercise 52).
Now, if we assume that the bulk of the mass of the tree is in the trunk, and if we model the trunk either as a long cylinder or as a thin cone, the mass is proportional to the volume, so M∝d2h. Then
at=M∝d2h∝(h3/2)2h=h4
so h∝t1/4. In other words, the tree grows in height as the fourth root of its age.
Question 18.82
52. Suppose that a tree grows to 10 m in 15 years. How tall will it be (if it lives long enough) when it is 60 years old?
Question 18.83
53. How long would it take the tree in Exercise 52 to grow to be 40 m tall?
53.
44=256 times as long, or 256×15=3840 years, so 3840−15=3825 more years.
Question 18.84
54. Giant sequoias can reach 100 m after about 1000 years. If it could keep on growing at the same rate of its addition of mass, how long would it take a giant sequoia 100 m tall to grow to 200 m?
Question 18.85
![]() 55. The branching of trees is similar to the branching of circulatory systems in the bodies of animals. For similar reasons, the area of the cross section of the tree at its base scales as the three-fourths power of the tree’s mass—that is, A∝M3/4. Assume that most of the mass is in the trunk and model the tree either as a tall cylinder (V=πr2h) or an elongated cone (V=πr2h/3). Show that the diameter d of a tree is approximately proportional to the three-halves power of the height—that is, d∝h3/2.
55. The branching of trees is similar to the branching of circulatory systems in the bodies of animals. For similar reasons, the area of the cross section of the tree at its base scales as the three-fourths power of the tree’s mass—that is, A∝M3/4. Assume that most of the mass is in the trunk and model the tree either as a tall cylinder (V=πr2h) or an elongated cone (V=πr2h/3). Show that the diameter d of a tree is approximately proportional to the three-halves power of the height—that is, d∝h3/2.
55.
A∝d2 and A∝M3/4∝(d2h)3/4=d3/2h3/4 so d2∝d3/2h3/4, hence d1/2∝h3/2.
18.5 How We Grow
Question 18.86
56. Listed below are the numbers of species of reptiles and amphibians on some Caribbean islands, together with the approximate areas of the islands. (Suggested by Florence Gordon of the New York Institute of Technology, with contributions from Kevin Mitchell and James Ryan of Hobart and William Smith Colleges, Geneva, New York. This table is adapted from Tables 15 and 16 in P. J. Darlington, Zoogeography: The Geographic Distribution of Animals, Wiley, New York, 1957, pp. 483-484.)
| Island | Area (mi2) | Species |
|---|---|---|
| Redonda | 1 | 3 |
| Saba | 4.9 | 5 |
| Montserrat | 40 | 9 |
| Trinidad | 2000 | 80 |
| Puerto Rico | 3400 | 40 |
| Jamaica | 4500 | 39 |
| Hispaniola | 30,000 | 84 |
| Cuba | 40,000 | 76 |
- Plot the number of species versus area on ordinary graph paper and then on log-log graph paper. If you don’t have log-log paper available, use a calculator or spreadsheet to take the logarithms (log10) of all the numbers and then graph logarithm of number of species versus logarithm of area on ordinary graph paper. (Note: Trinidad is an outlier from the general pattern; see Chapter 6.)
- (b) Is the relationship that you graphed in part (a) proportional? Is it allometric?
- What would be the expected number of species on an island of 400 mi2?
- For each 10-fold increase in the island’s size, what happens to the number of species, approximately?
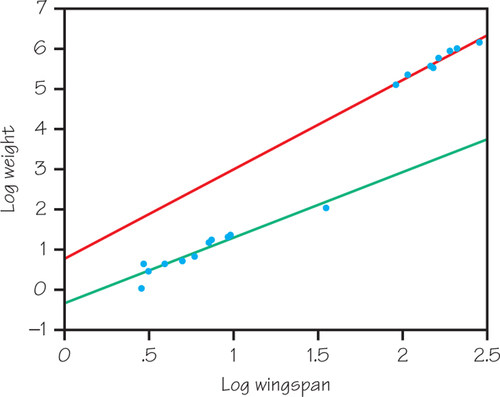
Question 18.87
57. The accompanying table lists the weights and wingspans of some birds and of some fully loaded airplanes. (Idea and most of the data contributed by Florence Gordon, New York Institute of Technology.)
- Use a calculator or spreadsheet to take the logarithms (log10) of all the numbers and then graph logarithm of weight versus logarithm of wingspan on ordinary graph paper.
- For the birds, is the relationship that you graphed in part (a) proportional? Is it allometric? How about for the planes?Page 774
Birds Weight (lb) Wingspan (ft) Crow 1 2.9 Harris hawk 2.6 3.2 Blue-footed booby 4 3 Red-tailed hawk 4 4 Horned owl 5 5 Turkey vulture 6.5 6 Eagle 12 7.5 Golden eagle 13 7.3 Whooping crane 16.1 7.5 Vulture 18.7 9.3 Condor 22 9.9 Quetzalcoatlus northropi 100 36 Planes Boeing 737 117,000 93 DC9 121,000 93.5 Boeing 727 209,500 108 Boeing 757 300,000 156.1 Boeing 707 330,000 145.7 DC8 350,000 148.5 Howard Hughes’s “Spruce Goose” 400,000 320.9 DC10 572,000 165.4 Boeing 747 805,000 195.7 Boeing 747-400 895,000 212.6 Anton An-225 1,323,000 290.2 - Does the same relationship of wingspan to weight seem to hold for birds and planes?
- A 25-million-year-old fossil recently discovered in South Carolina is of a seabird with a wingspan of 24 ft, Pelagornis sandersi. (That wingspan is larger than that of the largest living bird that can fly, the wandering albatross, 11 ft.) From your graph in part (a), what would you estimate the weight of a P. sandersi to have been?
57.
(a) The accompanying graph shows birds along the lower line (in green) and planes along the upper line (in red).
(b) Both relationships are allometric, since the results are good fits to straight lines whose slopes are not 1.
(c) The slope for birds is less steep than for planes.
(d) 64 lb
Question 18.88
58. Each December, the Friends of the Rock River Philharmonic raises funds with a holiday sale of poinsettia plants. The choices available, with cost in 2014 and average number of flowers per plant, are shown in the accompanying table.
| Diameter of Flowerpot | Average Number of Flowers | Cost |
|---|---|---|
| 6 in. | 6 | $11 |
| 7 in. | 9 | $18.75 |
| 8 in. | 18 | $30 |
- Plot on ordinary graph paper cost versus diameter of flowerpot. Do you observe linear scaling?
- Use a calculator or spreadsheet to take the base-10 logarithms (log10) of the cost and then graph the logarithm of cost versus diameter of flowerpot.
- Repeat parts (a) and (b) for cost versus average number of flowers.
- Use a model to estimate the number of flowers and the cost for a 9-in.-diameter flowerpot.
Chapter Review
Question 18.89
59. In the photo below of a statue of Paul Bunyan in Akeley, Minn., he would appear to stand about 33 ft tall and be geometrically similar to an ordinary muscular man.
- What is the linear scaling factor of the Paul Bunyan statue compared to a man 6 ft tall?
- If a man 6 ft tall weighs 200 lb, how much would Paul Bunyan weigh?

59.
(a) 5.5
(b) About 33,000 lb
Question 18.90
![]() 60. Some humans, such as the Bushmen of the Kalahari Desert in Africa, live in desert environments, where it is important to be able to do without water for periods of time. Would you expect such an environment to favor short people or tall ones? (Adapted from A. Zherdev, Horseflies and flying horses, Quantum, May-June 1994, 32-37, 59-60.)
60. Some humans, such as the Bushmen of the Kalahari Desert in Africa, live in desert environments, where it is important to be able to do without water for periods of time. Would you expect such an environment to favor short people or tall ones? (Adapted from A. Zherdev, Horseflies and flying horses, Quantum, May-June 1994, 32-37, 59-60.)
Question 18.91
![]() 61. Smaller birds and mammals generally maintain higher body temperatures than do larger ones. Explain why you would expect this to be so. (Adapted from A. Zherdev, Horseflies and flying horses, Quantum, May–June 1994, 32–37, 59–60.)
61. Smaller birds and mammals generally maintain higher body temperatures than do larger ones. Explain why you would expect this to be so. (Adapted from A. Zherdev, Horseflies and flying horses, Quantum, May–June 1994, 32–37, 59–60.)
61.
A small warm-blooded animal has a large surface-area- to-volume ratio. Pound for pound, it loses heat more rapidly than a larger animal and hence must produce more heat per pound, resulting in a higher body temperature.
Question 18.92
62. According to Time (March 7, 2005), men’s brains on average are 10% larger than women’s, even though men on average are only 8% taller. (The article mainly discusses the many differences in brain structure that likely outweigh any size differences.) If the brain scales linearly with height, and men are 8% taller, what percentage larger would you expect their brains to be? (And this consideration has nothing to do with relative intelligence!)
Question 18.93
63. A common measure of water in agriculture is the KAF, which is one thousand acre-feet. An acre-foot of water is the amount of water to cover a field of area one acre to a depth of one foot. A common measure of water usage in homes is the water billing unit, which is 748 gallons.
- How many gallons are there in 1 KAF?
- How much is one water billing unit in cubic feet? (Your water meter measures in cubic feet.)
- A typical two-person home in the Midwest uses about 100 water billing units per year. How much is that in KAF?
63.
(a) 326×106gal
(b) 100ft3 (that is the actual definition of a water billing unit)
(c) 2.3×10−4 KAF
Question 18.94
64. The largest animal ever to live is the blue whale. No blue whale has been weighed as a whole, but estimates are that the largest ones weigh 200 tons, are 30 m long, and have a lung volume of 5000 L. An adult human male 6 ft tall and weighing 200 lb has a lung capacity of about 6 L.
- If the human were scaled up to the height (length) of the whale, what would you project the lung volume to be?
- If the human were scaled up to the weight of the whale, what would you project the lung volume to be?
 What conclusions would you draw from the comparisons?
What conclusions would you draw from the comparisons?
Question 18.95
65. The U.S. Energy Security and Independence Act of 2007 required that 15 billion gallons of ethanol and other renewable fuels be blended with gasoline in 2015. In the United States, corn is the main source of ethanol. What percentage of total arable U.S. land (land that can be planted to crops) would be needed to raise that much corn ethanol? The contiguous United States (without Alaska or Hawaii) has hectares of arable land, which could yield about 400 gal/acre of ethanol.
65.
The arable land totals 667 million acres, which could produce gal; the 15 billion gal required would be of the total. In 2014, actual acreage planted to field corn was 92 million acres; at 400 gal/acre, that would supply 37 billion gal, so the ethanol would require about 40% of the corn crop.
Question 18.96
66. Unit conversion can matter, and the number of significant digits in the conversion factor can matter. New electronic components are designed using metric units, but accompanying circuit boards are often designed using U.S. customary units. Consider a connector with 100 pins on a side with design distance (“pitch”) of 0.6 mm from one pin to the next. (Thanks for the idea to Mark Biegert, Calix, Inc., Plymouth, Minnesota.)
- How far, in mm, is the 100 th pin from the first one?
- Use the conversion factor in., which is accurate to five decimal places and four significant digits, to calculate the distance in inches of the 100th pin from the first one. Then convert that quantity back to millimeters by using the exact conversion .
- Use the conversion factor in., which is accurate to three decimal places but only two significant digits, to calculate the distance of the 100th pin from the first one. Then convert that quantity back to millimeters by using the exact conversion . Will that last pin fit into a slot that is the exact distance of mm from the first pin?