18.5 18.4 Dimension Tension
A large change in scale forces a change in either materials or form. A major manifestation of this problem of scale is the tension between weight and the need to support it. For example, a real building or machine must differ from a scale model: The balsa wood or plastic of the model would never be strong enough for the real thing, which would need aluminum, steel, or reinforced concrete.
Another way to compensate is to redesign the object to distribute its weight better. Let’s go back to the original cube. It supports all its weight on its bottom face. In the version scaled up by a factor of 3, each small cube of the bottom layer has a bottom face supporting that cube’s weight plus the weight of the two cubes piled on top of it.
Let’s redesign the scaled-up cube, concentrating for simplicity only on the front face, with its nine small cubes. We take the three cubes on top and move them to the bottom, alongside the three that are already there. We take the three cubes on the second level, cut each in half, and put a half-cube over each of the six ground-level cubes (see Figure 18.9).
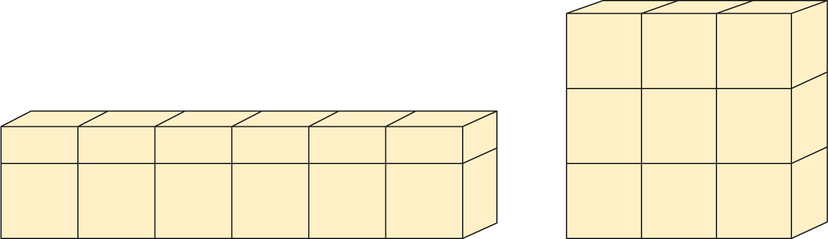
We have the same volume and weight that we started with, but now there is less pressure on the bottom face of each small cube.
Of course, the new design is not geometrically similar to the object that we started with; it’s no longer a cube. We have solved the scaling problem by changing the proportions.
We observe in nature both strategies for scaling: change of materials and change of form. Small animals (such as insects) do not have bony internal skeletons. Larger animals generally do. Animals made of similar materials but differing greatly in size, such as a mouse and an elephant, must differ in shape. If a mouse were scaled up to the size of an elephant, it would need the disproportionately thicker legs of the elephant to support its weight and the elephant’s thick hide to contain its tissue.
Some dinosaurs, like Supersaurus (which weighed 30 tons), had special adaptations to lighten their weight, such as hollow bones, just as some birds have. Hollow bones are stronger: Of two bones of the same weight and length, the hollow one is wider across at its midpoint because of the air it contains, and the greater the width, the greater the resistance to fracture.
Falls, Jumps, and Flight
The need to support weight can be thought of as a tension between volume and area. As an object is scaled up, its volume and weight go up together, so long as the density remains constant (e.g., no air bubbles introduced into the steel to make it into a Swiss cheese). At the same time, the ability to support the weight goes up with the cross-sectional area, like the bottom face of the steel cube.
Area-Volume Tension DEFINITION
Area-volume tension is a result of the fact that as an object is scaled up, the volume increases faster than the surface area and faster than areas of cross sections.
Because volume V is proportional to the cube of the linear scaling factor L, we have V∝L3; taking each side to the one-third power gives L∝V1/3. The fact that surface area A is proportional to the square of the linear scaling factor is expressed in our notation as
A∝L2∝(V1/3)2=V2/3
so that surface area scales as the two-thirds power of volume.

Natural and Fractional Exponents
In any crowded city, you can observe “parking tension”—tension between length, area, and volume. Consider an apartment building that spans a city block. The area of parking spaces on the adjacent streets is proportional to the perimeter of (length around) the building. But the number of cars belonging to people in the building is proportional to the number of apartments, which is proportional to the volume of the building. So the higher the building, the greater the parking tension.
In some cities, zoning puts shops on the ground floor, which cuts out one floor of apartments. If the residents’ cars are away during the day, customers and employees of the shops can park where the apartment dwellers do at night. A more common solution is an underground garage, with an area for cars proportional to the number of apartments, so in effect to the volume of the building. However, garages constructed with one car per apartment are inadequate now that families tend to have more than one car.
Other examples of the solutions to dimensional tension include the old- fashioned diner, with its serving counter in the form of an S-shape so as to expand its effective length, and your small intestine, which coils its 20-ft length to fit into your abdomen.
Though we can forget about humans “leaping tall buildings in a single bound,” “soaring like an eagle,” or “diving miles below the sea,” area-volume tension has many practical consequences related to those fantastical ideas. Consider the following examples.
EXAMPLE 8 Falls
Falls
Area-volume tension affects how animals respond to falling, another of gravity’s effects. How come a mouse may be unharmed by a 10-story fall, and a cat by a 2-story fall, but many humans are injured by falling while running, walking, or even just standing?
The explanation is that the energy acquired in falling is proportional to the weight of the falling object, and hence to its volume. This energy must be absorbed either by the object or by what it hits, or must be otherwise dissipated at impact—for example, as sound. The fall is absorbed over part of the surface area of the object, just as the weight of the cube was distributed over its base. With scaling up, volume—hence weight, hence falling energy—goes up much faster than area. As size increases, the hazards of falling from the same height increase.
EXAMPLE 9 Jumps
Jumps
A flea can jump as high as 50 cm (20 in.) vertically, many times its own height. Some people believe that if a flea were as large as a person, it could jump 1000 ft into the air. Is that so?
Imagining—against our earlier arguments—that there could be so large a flea, we can deduce its limits: A scaled-up flea could jump about the same height as a small flea. The strength of a muscle is proportional to its cross-sectional area (see Spotlight 18.3). A jump involves suddenly contracting the muscle through its length, so it turns out that the ability to jump is proportional to the volume of muscle. But the volume of the flea and the volume of its leg muscles would go up in proportion as we enlarged the flea to a geometrically similar giant flea.
Let’s say that a real flea’s leg muscles account for 1% of its body. If we scale the flea up to the size of a person (without any change in its form), the enlarged flea’s leg muscles will still make up 1% of its body. For either flea, each bit of muscle has the same power: In a jump, it propels 100 times its own weight, and it can do so to the same height. Both the weight of the flea and the power of its legs go up proportionately. In fact, the maximum heights that people, fleas, grasshoppers, and kangaroos can jump from standing are all within a factor of 3 of one another.
EXAMPLE 10 Flight
Flight
How does weight affect flight? After all, ostriches can’t fly.
Wouldn’t it be nice to be able to fly? Well, you have to be able to stay up. The power necessary for sustained flight is proportional to the wing loading, which is the weight supported divided by the area of the wings. We know that in scaling up, weight grows with the cube of the length of the bird or plane, and wing area with the square of the length. So the wing loading is proportional to the length of the flying object.

For example, if a bird or plane is scaled up proportionally by a linear scaling factor of 4, it will weigh 43=64 times as much but will have only 42=16 times as much wing area. So each square foot of wing must support 4 times as much weight. once you’re up, you have to keep moving. To stay level, an airborne object moving forward must fly fast enough to maintain the lift on the wings. It turns out that the minimum necessary speed is proportional to the square root of the wing loading. Combining this fact with the first consideration, we conclude that the minimum speed goes up with the square root of the length. A bird scaled up by a factor of 4 must fly √4=2 times as fast. (Hovering helicopters, hummingbirds, and insects maintain lift by moving their wings directly rather than relying on aerodynamic lift from forward motion.)
Take, for instance, a sparrow, whose minimum speed is about 20 miles per hour (mph). An ostrich is about 16 times as long as a sparrow, so the minimum speed for an ostrich would be √16×20=80 mph. Have you seen any flying ostriches lately? Heavy birds have to fly fast or not at all!
of course, ostriches are not just scaled-up sparrows, nor are eagles (nor are airplanes). Larger flying birds have disproportionately larger wings than a sparrow so as to keep the wing loading down.
The largest animal ever to take to the air was Quetzalcoatlus northropi, a flying reptile that lived 65 million years ago. It had a wingspan of 36 ft, weighed about 100 lb, and was as tall as a giraffe. Recent research suggests that it might have been able to “fly” 10,000 miles or more, nonstop, by taking advantage of air currents.
You have to stay up, you have to keep moving—and you have to get up there. Here, basic aerodynamics imposes further limits. Paleontologists originally thought that Q. northropi weighed 200 lb and had a 50-ft wingspan. Even though that works out to about the same wing loading as for 100 lb and a wingspan of 36 ft, other considerations from aerodynamics show that a reptile of the larger size couldn’t have gotten off the ground.
Self Check 6
The largest and heaviest aircraft in service today is the An-225—and we indeed mean “the” because there is only one! It was used to bring humanitarian equipment from Japan for Haiti, as well as—in a single flight—216,000 meals for U.S. military personnel. The plane has a wing area of 905m2 and a maximum takeoff weight of 1.3 million lb. Fully loaded, what would be its wing loading, in lb/ft2?
- 133 lb/ft2
Scaled to Fit 18.3
18.3
Big isn’t always beautiful when it comes to the U.S. military’s physical fitness tests.
Paul Vanderburgh, of the Department of Health and Sport Science at the University of Dayton, has spent more than a dozen years researching how a person’s body mass affects performance on such tests, which consist of distance runs, push-ups, sit-ups, and abdominal crunches. The Arnold Schwarzeneggers of the world actually tend to score lower.
Vanderburgh emphasizes that some larger people (like Schwarzenegger) have more muscle, not more fat. Nevertheless, he and fellow researcher Todd Crowder found that scores for larger and heavier (though muscular) men and women are 15% to 20% lower than for their smaller and lighter counterparts. “A person’s strength doesn’t increase as fast as their size,” explains student Liz Trouten. “The extra muscle that big people have doesn’t make up for their size.”
Vanderburgh noticed at the U.S. Military Academy that, even at similar fitness levels, smaller cadets tend to score higher on physical fitness tests than larger cadets. “Fitness testing is a big part of cadets’ grade point averages, and the stakes are pretty high. The test results affect class rank and even a cadet’s first assignment, so it matters a lot how well a cadet does.”
For example, a larger cadet with a fitness test score of 256, which Vanderburgh compares to a grade of C+, may not be eligible for certain awards and assignments. However, a smaller cadet with a perfect score of 300 “would get lots of attention.” But that doesn’t mean the C+ cadet isn’t worthy. “In fact, if these two cadets were scale models of each other, these two performances would be biologically the same, and they should receive the same score.”

Vanderburgh gives another example using the scale-model approach. Take a woman who is 5 feet 5 inches tall, weighs 130 pounds, and scores a perfect 300 on the fitness test. If she were 5 feet 8 inches tall and 30% heavier, she would score only 250.
To compensate for this body mass “penalty,” Vanderburgh and Crowder developed a correction factor, which multiplies the score by a number based on weight, “to place everybody on an even playing field.”
This formula is similar to the Flyer Handicap, developed by Vanderburgh and colleague Lloyd Laubach. The handicap adjusts a runner’s race time based on age and body weight. “A higher body weight is definitely a handicap for performance, whether it be running a marathon or military physical fitness tests,” Laubach said. (A web calculator for the Flyer Handicap is at http://academic.udayton.edu/PaulVanderburgh/weight_age_grading_calculator.htm.)
Source: Information from the article “Scaled to Fit,” by Kristen Wicker in the University of Dayton Quarterly (Winter 2006–2007), 21–22.
Keeping Cool (and Warm)
Area-volume tension is also crucial to an animal’s thermal equilibrium. Both warm-blooded and cold-blooded animals gain or lose heat from the environment in proportion to body surface area.
Warm-Blooded Animals
A warm-blooded animal’s basal metabolism, or rate of food intake needed to maintain body heat, depends primarily on its surface area, the temperature of its environment, and the insulation provided by its coat or skin. Other factors being equal, a scaled-up mammal scales up its food consumption with surface area (proportional to the square of the linear scaling factor), not with volume (proportional to its cube). For example, a mouse eats about half of its weight in food every day, while a human consumes only about one-fiftieth of its own weight, because the mouse has more surface area per unit volume.
Thus, the metabolic rate should be proportional to the surface area. Using proportionality notation, we can find how the metabolic rate changes with the mass of the animal. We know that mass is proportional to volume, which in turn is proportional to the cube of length, or
M∝V∝L3
Taking each side to the one-third power, we have
M1/3∝V1/3∝L, so L∝M1/3
Meanwhile, the metabolic rate (call it R) is proportional to surface area, so
R∝A∝L2,∝(M1/3)2=M2/3
So, based on area-volume tension, we would expect metabolic rate to scale as the two-thirds power of body mass. But it doesn’t—instead, it scales as the three-quarters power of body mass; that is, R∝M3/4. The least-squares line (see Section 6.4 on page 260) through the points in the “mouse-to-elephant” curve of Figure 18.10 has a slope of 0.74, very close to three-quarters. (The logarithmic coordinates used in this graph are explained in Section 18.5.)
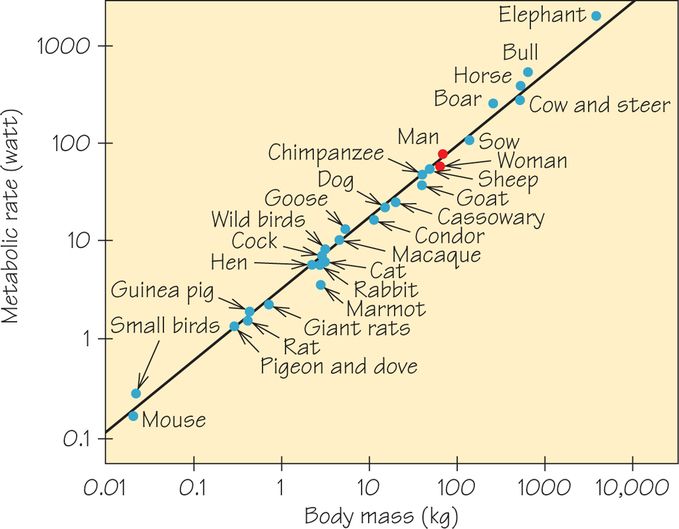
Why the difference from the two-thirds that area-volume tension would predict? And does the small difference between two-thirds and three-quarters matter? The answers lie in further considerations from geometry, physiology, and physics. A plant or animal needs a network of vessels (like the blood system) to transport resources to, and wastes away from, every part of the animal’s tissues. The terminal branches (capillaries in the blood system) tend to be just about the same size in all species, for reasons of the physics involved.
To minimize the energy involved in transport, the network of vessels needs to be organized as a fractal-like tree, with smaller and smaller vessels branching off. (See Section 19.5 to learn about fractal patterns.) With same-size smallest branches at the ends, it turns out that minimization of energy demands that the metabolic rate scale as the three-quarters power of body mass. Fractal branching makes it possible for the circulatory system of a whale, with 107 times the mass of a mouse, to have only 70% more branches than the mouse has.
EXAMPLE 11 Dives
Dives
Sperm whales (and some other species) regularly hold their breath and stay underwater for an hour. Why can’t we?
In part, it’s because we aren’t as large as whales. A mammal’s breath-holding ability depends on how much air it can hold in its lungs, which is proportional to its mass. It also depends on how fast it uses up air—in other words, on its metabolic rate, which is proportional to the three-quarters power of its mass. Hence, the limit of duration of a dive should be proportional to the volume of the air in the lungs divided by the rate of using up the air, or
MM3/4=M1/4
For a 90,000-lb sperm whale, this limit is proportional to 90,0001/4≈17.3, while the corresponding figure for a 150-lb human is 1501/4≈3.5. So the sperm whale should be able to hold its breath for about 17.3/3.5≈5 times as long. However, most humans cannot hold their breath for one-fifth of an hour (12 minutes)! (The record is 22 minutes; don’t try it—the guy died the next time he attempted it.) This fact tells us the whale has special adaptations to make long dives possible. The stars of the 2005 film March of the Penguins, emperor penguins, weigh 80 to 90 lb but can dive for as long as 20 minutes. Their special adaptations are more blood per pound of body weight, an abundance of myoglobin (which can store oxygen) in their tissues, and the slowing of their heart rate during dives.
Self Check 7
Consider a dolphin weighing 450 lb. If a whale can hold its breath for a certain length of time, for what fraction of that length of time should a dolphin be able to hold its breath? What does your calculation assume?
- About one-fourth as long; the calculation assumes that a dolphin is a “scaled-down” whale.
Cold-Blooded Animals
Mammals and birds regulate their metabolism and maintain a constant internal body temperature. Cold-blooded animals, such as alligators and lizards, have a somewhat different issue. They absorb heat from the environment for energy, but they must also dissipate any excess heat to keep their temperatures below unsafe levels. The amount of heat that must be gained or lost is proportional to total volume because the entire animal must be warmed or cooled. But the heat is exchanged through the skin, so the rate is proportional to surface area.
Dimetrodon was a large, mammal-like reptile that roamed present-day Texas and Oklahoma 280 million years ago (see Figure 18.11a).

Dimetrodon had a great “sail,” or fan, on its back. As an individual grew, and as the species evolved, the sail grew. But it did not grow according to geometric similarity, the kind of growth that is also called proportional growth.
Proportional Growth DEFINITION
Proportional growth is growth according to geometric similarity, where the length of every part of the organism enlarges by the same linear scaling factor.
Instead, the area of Dimetrodon’s sail grew in proportion to the volume of the animal, a fact that strongly suggests to paleontologists that the sail was a temperature-regulating organ. Larger specimens of Dimetrodon didn’t look like scaled-up smaller ones. We would say that the sail grew disproportionately compared with the rest of the animal. An individual twice as long would have 8(23) times as much weight and volume and a sail with 8 times as much area. If it had grown according to geometric similarity, the sail would have been twice as high and twice as wide, and hence would have had only 4 times as much area.
Dimetrodon was a large animal, but heat regulation is even more important for small animals; like human babies, they can lose heat quickly because of their high ratio of surface area to volume. Paleontologists believe that birds evolved from dinosaurs and that feathers are modified reptilian scales. The wings of birds and insects may have evolved not for flight but as temperature-control devices. Birds that live in hot climates, such as the toco toucan (Ramphastos toco), tend to have large bills and use them to lose heat by increasing bloodflow to the bill (see Figure 18.11b).
Some scientists have speculated that African pygmies are small in part because a small body can better lose heat in the hot, humid climate of the Ituri Forest in the Congo, where pygmies live. The discovery announced in late 2004 of “hobbit-sized” people (1 m tall) who lived on the island of Flores in Indonesia 13,000 years ago suggests another explanation. Being marooned on the island with a self-limiting food supply (they hunted pygmy elephants) made large size—and a corresponding need for more calories—a disadvantage.
Other scientists have suggested that ancestors of human beings began walking on two legs in part to keep cool in a hot climate. Walking upright exposes less body area to the rays of the sun than walking on all fours and also reduces the amount of water needed by about one-half.