Chapter 19 Exercises
Chapter 19 Exercises
19.1 Fibonacci Numbers and the Golden Ratio
Question 19.31
1. Examine the “scales” on the surface of a pineapple, which are arranged in spirals around the fruit in three distinct directions. For each direction, how many spirals are there?
1.
8, 13, and 21 for the usual pineapples in U.S. stores; 5, 8, and 13 or 6, 9, and 15 for other species.
Question 19.32
2. Repeat Exercise 1, but for a pinecone from your area.
Question 19.33
3. Repeat Exercise 1, but for a sunflower. (If you can’t obtain one, then count the spirals in Figure 19.1b.)
3.
Answers will vary but will be Fibonacci numbers.
Question 19.34
4. Here are two primitive models of natural increase of biological populations, similar to those that Fibonacci hypothesized around the year 1200, based on the following situation: A pair of newborn male and female rabbits is placed in an enclosure to breed.
- Suppose that the rabbits start to bear young one month after their own birth. At the end of each month, they have another male-female pair, which in turn mature and start to bear young one month later. Assuming that none of the rabbits die, how many pairs of rabbits will there be at the end of six months from the start (just before any births for that month)? (Hint: Draw a month-by-month chart of the situation at the end of the month, just before any births.)
- Repeat part (a), but assume instead that the rabbits start to bear young exactly two months after their own birth.
Question 19.35
5. Put the golden ratio ϕ=(1+√5)/2 into the memory of your calculator.
- Look at the value. Now square it (either use the x2 button or multiply it by itself). What do you observe?
- Go back to ÿ. Now take its reciprocal (either use the 1/x button or divide it into 1). What do you observe?
- What formula explains what you saw in part (a)?
- What formula explains what you saw in part (b)?
5.
(a), (b) The digits after the decimal point do not change.
(c) φ2=φ+1
(d) 1/φ=φ−1
Question 19.36
6. The golden ratio φ satisfies the equation x2=x+1. Show that (1−ϕ) also satisfies the equation, so that (1−ϕ) is the other solution to the equation.
Question 19.37
7. The geometric mean has interpretations in both arithmetic and geometry.
- Find the geometric mean of 3 and 27.
- Find the length of a side of a square that has the same area as a rectangle that is 4 by 64.
- You are to make a golden rectangle with 6 inches of string. How long should it be, and how wide?
7.
(a) 9
(b) 16
(c) Length ℓ=6/(2+2φ)≈1.15, width φℓ≈1.85; or vice versa.
Question 19.38
8. What is the geometric mean of 3, 9, 81, and 243?
Question 19.39
9. What is the geometric mean of 2, 4, 8, 16, and 32? (Such a sequence, in which each successive number is the same constant times the previous one, is called a geometric sequence.)
9.
8
Question 19.40
10. Using its recursion rule, extend the Fibonacci sequence to the left. For example, the value of F0 must satisfy F0+F1=F2, or F0+1=1, so F0=0. Using the same idea, find F−1,F−2,…,F−6.
Question 19.41
11. Another sequence closely related to the Fibonacci sequence is the Lucas sequence, which is formed using the same recursive rule but different starting numbers. The nth Lucas number Ln is given by
L1=1,L2=3, and Ln+1=Ln+Ln−1 for n≥2
- Calculate L3 through L10.
Calculate the ratio of successive terms of the Lucas sequence:
L2L1,L3L2,…L10L9
What do you notice?
11.
(a) 4, 7, 11, 18, 29, 47, 76, 123
(b) 3, 1.333, 1.75, 1.571, 1.636, 1.611, 1.621, 1.617, 1.618. The ratios approach φ.
Question 19.42
12. Repeat Exercise 11, but start with the pair of numbers 1 and 4.
Question 19.43
13. Repeat Exercise 11, but start with a pair of numbers of your choice. Based on your result and those in Exercises 11 and 12, what is your hunch?
13.
Answers will vary, but the ratio will always approach φ by alternating under- and overapproximations.
Question 19.44
14. For a sequence specified by a recursive rule, finding an explicit expression for the nth term is not easy, nor is the form necessarily simple. An exact expression for the nth term of the Fibonacci sequence is given by the Binet formula:
Fn=1√5(1+√52)n−1√5(1−√52)n
- Verify the formula for n=1 and n=2 by multiplying out, not by using a calculator.
- Use the Binet formula and your calculator to find F5.
- In fact, the second term on the right of the equation gets closer and closer to 0 as n gets large. Because we know that the Fibonacci numbers are integers, we can just round off the result of calculating the first term. Find F13 by calculating the first term with your calculator and rounding.
Question 19.45
![]() 15. For two positive numbers x and y, show that the arithmetic mean is always greater than or equal to the geometric mean. Try some values for x and y and convince yourself, then demonstrate algebraically that it is true in general. When does equality hold? [Hint: Suppose that the claim is false, so that (x+y)/2<√xy. Square both sides of the inequality, bring all terms to one side, factor, and observe a contradiction.]
15. For two positive numbers x and y, show that the arithmetic mean is always greater than or equal to the geometric mean. Try some values for x and y and convince yourself, then demonstrate algebraically that it is true in general. When does equality hold? [Hint: Suppose that the claim is false, so that (x+y)/2<√xy. Square both sides of the inequality, bring all terms to one side, factor, and observe a contradiction.]
15.
Answers will vary. Equality holds exactly when x=y.
Question 19.46
16. You may remember having to work problems like, “If Joe can dig a ditch in 3 days, and Sam can dig it in 4, how long will it take the two of them working together?” The answer is related to the harmonic mean of 3 and 4. The Environmental Protection Agency uses the harmonic mean to calculate the “average” fuel economy of the fleet of cars from a manufacturer. The formula for the harmonic mean of two numbers x and y is
21x+1y=2xyx+y
- Calculate the answer for Joe and Sam, which is one-half of the harmonic mean of 3 and 4. Explain why this is the correct answer. (In terms of fuel economy, using the harmonic mean assumes that each car is driven the same number of miles; using the arithmetic mean would assume that each car uses the same amount of fuel.)
 Show that the harmonic mean of two positive numbers is always less than or equal to the geometric mean. (Thus, in light of Exercise 15, we have the general conclusion that H≤G≤A, where H stands for the harmonic mean, G for the geometric mean, and A for the arithmetic mean.) (Hint: Suppose that the claim is false. Simplify the fraction that is the harmonic mean, square both sides of the inequality, and proceed as in Exercise 15.)
Show that the harmonic mean of two positive numbers is always less than or equal to the geometric mean. (Thus, in light of Exercise 15, we have the general conclusion that H≤G≤A, where H stands for the harmonic mean, G for the geometric mean, and A for the arithmetic mean.) (Hint: Suppose that the claim is false. Simplify the fraction that is the harmonic mean, square both sides of the inequality, and proceed as in Exercise 15.) Show once more that the harmonic mean of two positive numbers is always less than the geometric mean, but this time do it with less work: Let A=1x and B=1y, and discover one connection (equation) between the harmonic mean of x and y and the arithmetic mean of A and B, and a second connection between the geometric mean of x and y and the geometric mean of A and B. Then use Exercise 15 on A and B.
Show once more that the harmonic mean of two positive numbers is always less than the geometric mean, but this time do it with less work: Let A=1x and B=1y, and discover one connection (equation) between the harmonic mean of x and y and the arithmetic mean of A and B, and a second connection between the geometric mean of x and y and the geometric mean of A and B. Then use Exercise 15 on A and B. What should be the formula for the harmonic mean of three numbers? Of n numbers?
What should be the formula for the harmonic mean of three numbers? Of n numbers?
Question 19.47
17. New houses are to be built along one side of a street (Leonardo’s Lane), divided into equal-sized lots. Each house is either a single-family detached house, taking up one lot, or a duplex, taking up two lots. Suppose that there are n lots on the street. How many different arrangements (orderings) of houses are there, for n=1,2,3,4,5, and in general? (This exercise was inspired by a puzzle by Paul Dixon at the website by Ron Knott, cited in the Suggested Websites at the end of this chapter.)
17.
Question 19.48
18. When it snows in the winter, the local school district superintendent must decide by 5 A.M. whether to declare a snow day and cancel school. The 900 faculty and staff are now notified by a robocall broadcast, but formerly a binary “telephone tree” was used, in which the superintendent called two people and each person who received a call called two others. Suppose that each call takes exactly 1 minute.
- Draw the telephone tree of calls for, and determine how many calls take place in, the first 1 minute, 2 minutes, 3 minutes, 4 minutes, and 5 minutes.
- How many calls does it take to notify all the faculty and staff? How long does that take?
(This exercise was inspired by a puzzle at the website by Ron Knott.)
Question 19.49
19. Here is a trick to “prove” that you can calculate faster than a person with a calculator. Turn your back and ask a friend to write down any two positive integers, then add them to get a third, then add the second and third to get a fourth, and so on, adding each time the last two integers until there are 10 numbers. Have your friend show you the list, whereupon you write down right away the total of all 10, while your friend begins to add them up on the calculator (to prove that you’re right). The secret: The total is always 11 times the seventh number, and multiplying by 11 is fairly easy to do in your head—just add each pair of neighboring digits, carrying if necessary. Suppose that your friend writes down and as the first two numbers. Show that indeed the total of all 10 numbers is 11 times the seventh number. (Adapted from Martin Gardner, Mathematical Circus, Knopf, New York, 1979.)
19.
The seventh number is , and the total is .
Question 19.50
![]() 20. The game of Fibonacci Nim begins with counters. Two players take turns removing at least one counter, but no more than twice as many as the opponent just did. The winner is the player who takes the last counter. One other rule: The first player may not win immediately by taking all the counters on the first turn. (Adapted from Martin Gardner, Mathematical Circus, Knopf, New York, 1979.)
20. The game of Fibonacci Nim begins with counters. Two players take turns removing at least one counter, but no more than twice as many as the opponent just did. The winner is the player who takes the last counter. One other rule: The first player may not win immediately by taking all the counters on the first turn. (Adapted from Martin Gardner, Mathematical Circus, Knopf, New York, 1979.)
- Play this game taking turns with an opponent and starting with different numbers of counters and try to come up with a strategy for one player or the other to win. (Hint: The key is that any positive integer can be represented uniquely as a sum of Fibonacci numbers.)
- Proceed as in part (a), but with the rule changes that the player who takes the last counter loses and the first player may not take all but one counter.
Question 19.51
21. Shari Lynn Levine, as a high school student, published an article in The Fibonacci Quarterly that investigated the “Beta-nacci” sequence that results if, instead of bearing one pair of baby rabbits per month, mature rabbits bear two pairs every month, starting when they reach two months of age. Here, we ask you to rediscover some of Shari’s results.
- How many rabbits will there be each month for the first 12 months?
- What is the recursive rule for the nth Beta-nacci number ?
- For the terms of the sequence in part (a), calculate the ratios of successive terms. (Motivating hint: It’s not the golden ratio this time.)
 Suppose that the ratio of successive terms approaches a number . We show how to find exactly. For very large , we have . Inserting these values into the recursive rule for the sequence and dividing by gives the equation . Solve this equation for (you can use the quadratic formula). Make a table of values of versus . From the evidence, can you suggest a formula for ?
Suppose that the ratio of successive terms approaches a number . We show how to find exactly. For very large , we have . Inserting these values into the recursive rule for the sequence and dividing by gives the equation . Solve this equation for (you can use the quadratic formula). Make a table of values of versus . From the evidence, can you suggest a formula for ?
21.
(a) 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, 683, 1,365
(b)
(c) 1, 3, 1.667, 2.2, 1.909, 2.048, 1.977, 2.012, 1.994, 2.003, 1.999
(d) ; we discard the root.
Question 19.52
![]() 22. Generalize Exercise 21, parts (a) through (d), as follows:
22. Generalize Exercise 21, parts (a) through (d), as follows:
- to the case of each pair of rabbits having three pairs of rabbits (the “Gamma-nacci” sequence).
- to the case of each pair of rabbits having pairs of rabbits.
For Exercises 23 and 24, refer to the following. We have seen that the golden ratio is a positive root of the quadratic polynomial . We can generalize this polynomial to for and consider the positive roots of those polynomials as generalized means—the metallic means family, as they are sometimes known. In particular, for , and 5, we have, respectively, the silver, bronze, copper, and nickel means. It is surely surprising that these numbers arise both in connection with quasicrystals (investigated in Chapter 20) and in analyzing the behavior of some dynamical systems (investigated in Chapter 23) as the systems evolve into chaotic behavior.
Question 19.53
23. Use the quadratic formula to find expressions in terms of square roots for the silver, bronze, copper, and nickel means, and approximate these to three decimal places. Find a general expression in terms of a square root for the th metallic mean.
23.
Silver mean: ; bronze mean: ; copper mean: ; nickel mean: . General expression:
Question 19.54
24. Just as the golden mean arises as the limiting ratio of consecutive terms of the Fibonacci sequence, each of the metallic means arises as the limiting ratio of consecutive terms of generalized Fibonacci sequences. A generalized Fibonacci sequence can be defined by
where and are positive integers. The Fibonacci sequence itself is the case .
- Try various small values of and and determine which means they lead to.
 Divide the equation for by . Assume that and both tend toward the same number as gets large, replace those quantities by , and simplify the resulting equation. What must be the value of ?
Divide the equation for by . Assume that and both tend toward the same number as gets large, replace those quantities by , and simplify the resulting equation. What must be the value of ?- What happens to the sequence and to the mean if we allow one or both of and to be negative integers?
19.2 Rosette and Strip Patterns
Question 19.55
25. Determine whether each of the following statements is always or sometimes true. Drawing some sketches may be helpful.
- A line reflection preserves collinearity of points. That is, if the points , , and are in a straight line (collinear), then their images reflected in some other line also lie in a straight line.
- A line reflection preserves betweenness. That is, if the collinear points , , and (with between and ) are reflected about a line, then the image of is between the images of and .
- The image of a line segment under a line reflection is a line segment of the same length.
- The image of an angle under a line reflection is an angle of the same measure.
- The image of a pair of parallel lines under a line reflection is a pair of parallel lines.
25.
All are always true.
Question 19.56
26. Determine whether each of the following statements is always or sometimes true. Drawing some sketches may be helpful.
- The image of a pair of perpendicular lines under a line reflection is a pair of perpendicular lines.
- The image of a square under a line reflection is a square.
- Label the vertices of a square , , , and in a clockwise direction. Then their images , and under a line reflection also follow a clockwise direction.
- The length of the perimeter of a geometric figure is equal to the length of the perimeter of its image under a line reflection.
- The image of a vertical line under a line reflection is always a vertical line.
Question 19.57
27. Which of the capital letters of the alphabet, when drawn in the most symmetrical way, have the following symmetries? For example, assume that the upper and lower loops of B are the same size.
- A horizontal line of reflection symmetry
- A vertical line of reflection symmetry
- A rotational symmetry
27.
(a) B, C, D, E, H, I, K, O, X
(b) A, H, I, M, O, T, U, V, W, X, Y
(c) H, I, N, O, S, X, Z
Question 19.58
28. Repeat Exercise 27 for the lowercase letters.
Question 19.59
29. In The Complete Walker III (3d ed., Knopf, New York, 1984, p. 505), Colin Fletcher’s answer to “What games should I take on a backpacking trip?” is the game he calls “Colinvert”: “You strive to find words with meaningful mirror (or half-turn) images.” Some of the words he found are as follows:
- Which of his words reflect into themselves?
- Which of his words rotate into themselves?
- Find some more words or phrases of these various types—the longer, the better.
29.
(a) MOM, WOW; MUd and bUM reflect into each other, as do MOM and WOW.
(b) pod rotates into itself; MOM and WOW rotate into each other.
(c) Here are some possibilities: NOW NO; SWIMS; CHECK BOOK BOX; OX HIDE.
Question 19.60
30. Repeat Exercise 29, but for words written vertically instead of horizontally.
Question 19.61
31. For each of the following patterns, identify the rigid motions that preserve the pattern:
- CCCCCCCCCC
- GGGGGGGGGG
- HHHHHHHHHH
- MMMMMMMMMM
31.
For all parts, translations.
(a) Reflection in the horizontal midline
(b) None other than translations
(c) Reflection in the horizontal midline, reflections in vertical lines through the centers of the Hs or between them, 180° rotation around the centers of the Hs or the midpoints between them, glide reflections.
(d) Reflections in vertical lines through the centers of the Ms or between them.
Question 19.62
32. Repeat Exercise 31, but for the following patterns:
- SSSSSSSSSS
- bdbdbdbdbd
- dbpqdbpqdbpq
19.3 Notation for Patterns
Question 19.63
33. What is the notation for the symmetry pattern of a regular pentagon (which has all five sides equal)—, , or something else?
33.
Question 19.64
34. What is the notation for the symmetry pattern of a snowflake with six symmetrical arms, with each arm having mirror symmetry?
Question 19.65
35. Give the notation (such as or ) for the symmetry patterns of the rosettes in hubcaps (a) through (c) below, disregarding the logos in the centers.
35.
(a) (Audi)
(b) without considering bolts, with bolts (BMW)
(c) (Renault)
Question 19.67
37. Repeat Exercise 35 for corporate logos (a) through (c) below. (Bonus: Can you identify the corporations?)
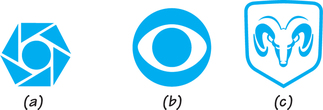
37.
(a)
(b) (CBS)
(c) (Dodge Ram)
For Exercises 39–40, refer to the following. Step patterns are found in Celtic illuminated manuscripts, metalwork, and stone crosses. Square ones were constructed by first designing on a square lattice one- quarter of the pattern (say, the top right), using horizontal and diagonal lines to produce a prototype such as the following:

Then three copies were added, either by (1) rotating the original successively by 90° [as in accompanying illustration (a)], or else by (2) reflecting it across its right and bottom edges [as in illustration (b)]. (Based on research by Mark A. M. Lynch of Glasgow Caledonian University, Scotland.)
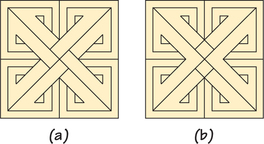
Question 19.69
39. Identify the rosette pattern for
- step pattern (a).
- step pattern (b).
39.
(a)
(b)
Question 19.70
40. Which rosette pattern would result if the prototype, unlike the one above, has reflection symmetry across its diagonal from the top left to the lower right and
- strategy (1) is used.
- strategy (2) is used.
Question 19.71
41. Use the flowchart in Figure 19.13 (page 799) to identify the notation for the types of strip patterns from the pottery and basketry shown in the illustrations on the next page.

41.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Question 19.72
42. In each of the four accompanying examples, two adjacent triangles of an infinite strip are shown. (Contributed by Margaret A. Owens, California State University, Chico.)
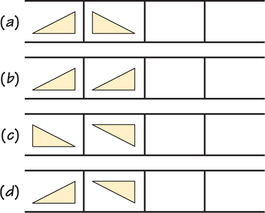
For each example:
- Determine a motion (translation, reflection, rotation, or glide reflection) that takes the first (left) triangle to the second (right) one.
- Draw the next four triangles of the infinite strip that would result if the second triangle is moved to the next space by another motion of the same kind, and so on.
- Identify (by notation) the resulting strip as one of the seven possible strip patterns.
Question 19.73
43. Repeat Exercise 41 for the accompanying eight strip patterns, all of which appear on the brass straps for a single lamp from 19th-century Benin in West Africa. (From H. Ling Roth, in Great Benin.)
Pottery and basketry from the Americas. (a), (b) Mexico, modern.
(c) Lower Central America, pre-Columbian.
(d) Pomo people, California, early 20th century.
(e) Woodland Indians, central North America, early 20th century.
(f) Pomo people, California, mid-20th century; originally from the collection of Dr. Herbert Zim, editor of the Golden Guides series of nature books.
(g) Woodland Indians, central North America, early 20th century.
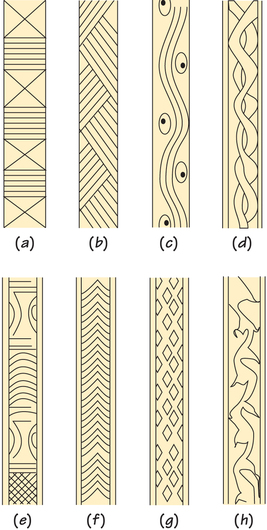
Note that the patterns are roughly carved, so you will need to discern the intent of the artist.
43.
(a)
(b)
(c)
(d)
(e) (perhaps)
(f)
(g)
(h)
Question 19.74
44. Repeat Exercise 41 for the accompanying patterns from San Ildefonso Pueblo, New Mexico.
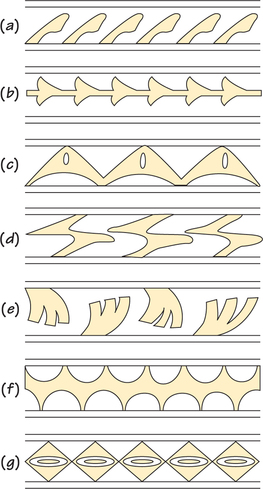
Question 19.75
45. The following table shows comparative data about the frequency of occurrence of strip designs of various types on Chinese porcelain and smoking pipes (Begho, in what is now Ghana) from two continents.
| Yuan (1280–1368) and Ming (1368–1644) Dynasties | ||
|---|---|---|
| Strip Type | Number of Examples | Percentage of Total |
| p111 | 29 | 18 |
| pimi | 1 | 1 |
| pm11 | 66 | 42 |
| p112 | 20 | 13 |
| p1a1 | 21 | 13 |
| pma2 | 13 | 8 |
| pmm2 | 9 | 6 |
| TOTAL | 159 | |
| Begho | ||
|---|---|---|
| Strip Type | Number of Examples | Percentage of Total |
| p111 | 4 | 2 |
| p1m1 | 9 | 4 |
| pm11 | 22 | 10 |
| p112 | 19 | 8 |
| p1a1 | 2 | 1 |
| pma2 | 9 | 4 |
| pmm2 | 165 | 72 |
| TOTAL | 230 | |
- Which types of motions appear to be preferred for designs from each of the two localities?
- What other conclusions do you draw from the data of this table?
- On the evidence of the table alone, in which locality is each of the following strip patterns (but not necessarily the motif) most likely to have been found?
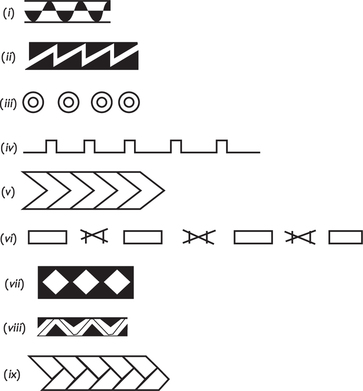
45.
(a) Patterns with vertical reflections are preferred on the Chinese pieces, while patterns with both horizontal and vertical reflections are strongly preferred on the Begho pipes.
(b) Neither culture completely excludes any strip type.
(c) (i) or : China. (ii) : China. (iii) : Begho. (iv) : China. (v) : Begho. (vi) : Begho. (vii) : Begho. (viii) : China. (ix) : China.
Question 19.76
![]() 46. For the Nigerian Yoruba cloths (a) and (b) in the following illustration, use the flowchart in Spotlight 19.9 (page 797) to identify (by notation) the type of wallpaper pattern.
46. For the Nigerian Yoruba cloths (a) and (b) in the following illustration, use the flowchart in Spotlight 19.9 (page 797) to identify (by notation) the type of wallpaper pattern.

Patterns on Yoruba (West Africa) adire cloth, made by starching a pattern onto white cloth, then dyeing the cloth before rinsing out the starch, so that the starched portion remains as a white design against a colored background.
Question 19.77
![]() 47. For the Nigerian Yoruba cloths (c) and (d) in the accompanying illustration, use the flowchart in Spotlight 19.9 (page 797) to identify (by notation) the type of wallpaper pattern.
47. For the Nigerian Yoruba cloths (c) and (d) in the accompanying illustration, use the flowchart in Spotlight 19.9 (page 797) to identify (by notation) the type of wallpaper pattern.
47.
(c) Smallest rotation is 90°, there are reflections, there are reflections in lines that intersect at 45°: .
(d) Smallest rotation is 90°, there are no reflections: .
Question 19.78
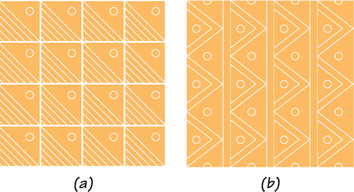
48. For the floor tilings (a) and (b) below, use the flowchart in Spotlight 19.9 (page 797) to identify (by notation) the type of wallpaper pattern.

Question 19.79
49. For the floor tilings (c) and (d) that follow, use the flowchart in Spotlight 19.9 (page 797) to identify (by notation) the type of wallpaper pattern.

49.
(c)
(d) Regarding the red/brown shapes as squares: , if color is disregarded; otherwise .
Question 19.80
![]() 50. The triangles in the grid at the top of the following figure show the beginning steps in forming instances of several of the wallpaper patterns by putting together a vertical motion and a horizontal motion.
50. The triangles in the grid at the top of the following figure show the beginning steps in forming instances of several of the wallpaper patterns by putting together a vertical motion and a horizontal motion.
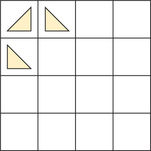
- Identify the horizontal motion.
- Identify the vertical motion.
- Fill in the remaining empty squares.
- Identify the wallpaper pattern.
Question 19.81
![]() 51. Which of the 17 wallpaper patterns can be formed by the technique used in Exercise 50?
51. Which of the 17 wallpaper patterns can be formed by the technique used in Exercise 50?
51.
None of the five patterns with hexagonal symmetry can be realized, nor any of , , , and . The remaining eight can all be formed by the technique.
For Exercises 52–57, refer to the following. In Chapter 20, we study both repeating and nonrepeating plane patterns, from the point of view of their basic building blocks (tiles). Here, we ask you to analyze the repeating patterns from figures in that chapter according to wallpaper type, using the flowchart of Spotlight 19.9 (page 797). Identify all the symmetries and give the notational type for the wallpaper pattern of the illustrations that follow.
Question 19.82
![]() 52.Figure 20.10 (page 837)
52.Figure 20.10 (page 837)
Question 19.84
![]() 54.Figure 20.16 (page 841)
54.Figure 20.16 (page 841)
Question 19.85
![]() 55. The figure in Spotlight 19.9 (page 836)
55. The figure in Spotlight 19.9 (page 836)
55.
Question 19.86
![]() 56. The hexagonal regular tiling at upper right in Figure 20.5 (page 831)
56. The hexagonal regular tiling at upper right in Figure 20.5 (page 831)
Question 19.88
![]() 58. Visit the website escher.epfl.ch/escher/, which features an interactive Java program called Escher Web Sketch. Experiment with choosing wallpaper patterns using crystallographic notation. For each one, draw on the screen a colored design for the motif; the program will reproduce the motif using the pattern.
58. Visit the website escher.epfl.ch/escher/, which features an interactive Java program called Escher Web Sketch. Experiment with choosing wallpaper patterns using crystallographic notation. For each one, draw on the screen a colored design for the motif; the program will reproduce the motif using the pattern.
19.4 Symmetry Groups
Question 19.89
59. For positive integers and , the expression mod means the remainder when is divided by . Thus, , because , and we say that “23 is equivalent to 3 modulo 4.” (See Chapter 17 for further details about this modular arithmetic.) Every positive integer is equivalent to 0, 1, 2, or 3 modulo 4. Consider the collection of elements {0, 1, 2, 3} and the operation on them defined by mod 4. Show that under this operation, the collection forms a group.
59.
Answers will vary.
Question 19.90
60. Explain, by referring to the properties of a group, whether the collection of all real numbers is a group under the operation of (a) addition and (b) multiplication.
Question 19.91
61. Explain why the table for the operation * below shows that the elements indicated do not form a group under *.
| * | |||
61.
There is no identity element.
Question 19.92
62. Consider the table below for an operation #.
| # | ||||||
- Explain why the elements form a group under #. (Don’t bother to check associativity.)
- What do you notice about # versus # ? (This is the smallest example of a group that is noncommutative.)
Question 19.93
63. Construct the table for the mattress group of Example 6 on page 804, putting down the side of the table the first turn made and, across the top of the table, the subsequent turn.
63.
| I | F | R | T | |
| I | I | F | R | T |
| F | F | I | T | R |
| R | R | T | I | F |
| T | T | R | F | I |
Question 19.94
64. The mattress group is a commutative group, meaning that the order of the turns doesn’t make any difference. How can you tell that from the table of Exercise 63? [A commutative group is sometimes called an abelian group, after Niels Henrik Abel (1801–1829), a Norwegian mathematician who died of tuberculosis at a young age.]
Question 19.95
65. A problem about mattress turning is that people usually don’t remember the immediately previous position or immediately previous turn that they made months ago. So the next time, they could wind up just turning the mattress back to the position that it was in only two seasons ago. Show that the mnemonic “Spin in spring, flip in fall” (courtesy of Bill Sandidge of Atlanta, Georgia), in fact, cycles the mattress through its four positions.
65.
The notation of Example 6 uses for flip, (rotation) for spin. Start in summer in the upper left position of the figure for Example 6 and follow the arrows: The in the fall brings the mattress to the position in the upper right, following that by takes it to the position in the lower left, doing another brings it to the position in the lower right, and yet another brings it back to the original position at upper left.
Question 19.96
66. A king mattress is officially , which is almost square. Make yourself a “square mattress” from a sheet of paper and investigate its group.
- What are the possible turns for a square mattress?
- Make a table for this mattress group.
Question 19.97
67. Show that the collection of numbers {1, 3, 5, 7} under multiplication modulo 8 (see Exercise 59) has the structure of the Klein 4-group (page 805).
67.
Answers will vary.
Question 19.98
68. Show that the dihedral rosette group has the structure of the Klein 4-group.
For Exercises 69–72, refer to the following. Like mattresses, car tires need to be rotated so as to promote even wear; wear on a tire varies with wheel position. The three main rotation schemes are shown below.
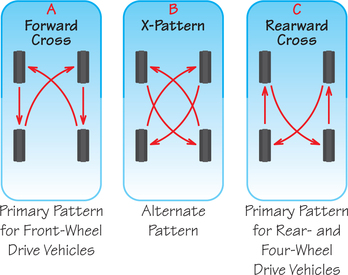
Question 19.99
69.  Show that successive tire rotations using scheme A form a group. Is it the Klein 4-group (page 805)?
Show that successive tire rotations using scheme A form a group. Is it the Klein 4-group (page 805)?
69.
Answers will vary. No, it is the cyclic group of order 4—e.g., the tire at position 1 goes to 3, then to 2, then to 4, and then back to 1.
Question 19.100
70. Observe that repeating scheme B will never take the front right tire to the back right wheel. Is there any combination of schemes A and C that will produce the result of scheme B?
Question 19.101
71. A tire rotation scheme is designed so that no tire will remain where it was. Such a rearrangement (permutation) of objects is called a derangement. Two more tire rotation schemes are shown below. Are there still more schemes that are derangements? One way to record a tire rotation is to label the original tire positions clockwise from the left front: 1 for left front, 2 for right front, 3 for right rear, and 4 for left rear. Record the results of a scheme by writing in turn where each tire goes; for example, scheme D below produces the derangement 4321 because tire 1 goes to position 4, tire 2 goes to position 3, and so forth.
71.
There are four more derangements: , where CW stands for clockwise and CCW for counterclockwise.
Question 19.102
72. Do the five tire rotation schemes A, B, C, D, and E, plus the identity rotation and any others that you found in Exercise 69, form a group? Why or why not?
Question 19.103
73. For the traditional North American beadwork shown below, answer the following questions.
- Which rosette pattern does it have?
- Specify two rigid motions that together generate the group of the pattern.
- List the elements of the group.

73.
(a)
(b) Any two of: (180° rotation around the center), (reflection in vertical line through its center), (reflection in horizontal line through its center).
(c)
Question 19.105
75. What are the elements for the group of symmetries of a square?
75.
There are four rotational symmetries (including the identity), two reflection symmetries, and two reflections across diagonal lines:
.
Question 19.106
76. Using the notation of rosette patterns, describe the group of symmetries of
- an equilateral triangle (all three sides equal).
- an isosceles triangle (two equal sides) that is not equilateral.
- a scalene triangle (no pair of sides equal).
Question 19.107
77. (a) Give a numerical example to show that the operation of subtraction on the integers is not associative.
(b) Repeat part (a), but for division on the positive real numbers.
77.
Answers will vary.
Question 19.108
78. What are the elements of the group of symmetries of
- Figure 19.11b?
- Figure 19.11f? (See page 795 for these images.)
Question 19.109
79. What are the elements of the group of symmetries of
79.
As in Example 6, number fixed positions, label with letters copies of the pattern elements in the positions, and pick a fixed position about which to make a half-turn .
(a) .
(b) .
Question 19.110
80. What are the elements of the group of symmetries of the dihedral pattern ? (See the flower in Figure 19.10a on page 794.)
Question 19.111
81. What are the elements of the group of symmetries of the cyclic pattern ?
81.
, where is a rotation by 45°.
Question 19.112
![]() 82. What is the group of symmetries of a cube?
82. What is the group of symmetries of a cube?
Question 19.113
![]() 83. What is the group of symmetries of a general rectangular solid (its length, width, and height are all unequal)?
83. What is the group of symmetries of a general rectangular solid (its length, width, and height are all unequal)?
83.
There are four rotational symmetries (including the identity), three reflection symmetries, and an inversion through the center that swaps diagonally opposite corners.
19.5 Fractal Patterns and Chaos
Question 19.114
![]() 84. Explore Sprott’s Fractal Gallery at sprott. sprott.physics.wisc.edu/fractals.htm, which features a “Fractal of the Day” and accompanying fractal music. There are various “rooms” in the gallery—including “Iterated Function Systems,” “Natural Fractals” (we particularly like “Broccoli” and “Trees”), and “Publication Quality Attractors” (“SMKBNZQA” is our favorite)— together with PC programs for generating such fractals. What are your favorites, and why?
84. Explore Sprott’s Fractal Gallery at sprott. sprott.physics.wisc.edu/fractals.htm, which features a “Fractal of the Day” and accompanying fractal music. There are various “rooms” in the gallery—including “Iterated Function Systems,” “Natural Fractals” (we particularly like “Broccoli” and “Trees”), and “Publication Quality Attractors” (“SMKBNZQA” is our favorite)— together with PC programs for generating such fractals. What are your favorites, and why?
Question 19.115
85. Explain how the pattern of the following illustration is fractal.
85.
The green branches have, in turn, smaller branches extending from them, and even smaller ones branch from those.
Exercises 86–88 use applets that require a computer with a web browser equipped with Java and Flash plug-ins. These plug-ins are available at links from the website csdt.rpi.edu/.
Question 19.116
86. The website csdt.rpi.edu/African/MANG_DESIGN/culture/mang_homepage.html offers information about a fractal-patterned ivory hatpin from the Mangbetu culture in Africa. The site includes a tutorial on producing similar designs using reflection, rotation, translation, and scaling. Work your way through the tutorial and then create a Mangbetu-style artifact.
Question 19.117
87. Cornrow hairstyles are fractal in nature. At the website csdt.rpi.edu/african/CORNROW_CURVES/, you can see how and why, including a tutorial on designing cornrow hairstyles using reflection, rotation, translation, and scaling. Work your way through the tutorial and then create a hairstyle. The website also includes instructions for actual braiding, with a short video.
87.
Answers will vary.
Question 19.118
88. Download fractal-creation software and accompanying documentation and use the software to create your own fractal. Links to software, most of it free, are available at www.Nahee.com/PNL/Fractal_Software.html and at fractalfoundation.org/resources/fractal-software/. Recommended software:
For Windows: Fractint, from www.Nahee.com/spanky/www/fractint/fractint.html
For Macintosh: XaoS, a fractal zoomer, from fractalfoundation.org/resources/fractal-software/.
Chapter Review
Question 19.119
89. You have 42 in. of string that you want to use as the perimeter of a rectangle whose sides have lengths in inches that are Fibonacci numbers. What are the dimensions of your rectangle?
89.
Question 19.120
90. Identify the rigid motions that preserve the pattern of DDDDDDDD.
Question 19.121
91. What is the notation for the symmetry pattern of DDDDDDDDD?
91.
Question 19.122
92. What is the notation for the symmetry pattern of the pinwheel below?

Question 19.123
93. For the floor tiling below, use the flowchart in Spotlight 19.9 (page 797) to identify (by notation) the type of wallpaper pattern.

93.
Question 19.124
94. Do the real numbers form a group under division?
Question 19.125
95. What are the elements of the group of symmetries of rosette pattern ?
95.
The pattern is the pattern of symmetries of an equilateral triangle. Let be a clockwise rotation of 120° about the center and let be a reflection about the vertical line of symmetry. Then the elements of the group are . To convince yourself, label the vertices , and , and apply the symmetries.


