Left to its own devices, a free market with externalities produces more than (if the externalities are negative) or less than (if the externalities are positive) the optimal welfare-maximizing quantity. As a result, the market generates deadweight losses when a good has negative or positive externalities.

Is society doomed to live with this inefficiency? Not necessarily. Just as we saw in Chapter 16 that asymmetric information’s potential welfare losses offer powerful incentives to create institutions that remedy them, the same is true for externalities. Governments or the economic actors in markets with externalities may implement one of several interventions that can reduce the inefficiencies externalities create.

Externality fixes come in two basic types: those that work through their effect on price and those that work through their effect on quantity. Both types try to steer the market away from the inefficient outcome of the private market (in which only private marginal costs and benefits are considered) toward the more efficient outcome (in which social marginal costs and benefits are considered). The price approach pushes prices to reflect the true social costs and benefits. The quantity approach pushes quantities toward efficient levels.

Because many real-world solutions to externalities occur to try to correct for the ill effects of pollution, we focus on that particular negative externality throughout this section.

Before considering how to correct for an externality, we need to consider how the government chooses its efficiency target. The goal is to set the level of total pollution allowable at its efficient level. The efficient level of pollution is the level of emissions necessary to produce the efficient quantity of the good tied to the externality. Therefore, the total amount of emissions allowable is set at the level that allows the market for the good to produce the quantity at which demand equals marginal social cost.

We can also think about the efficient amount of pollution (or any negative externality) as the level that balances its costs and benefits. Pollution’s costs—the health implications and such—are easy to grasp. Pollution’s “benefits” derive from the fact that some pollution is a necessary by-product of the production of goods, like electricity. To ban pollution would mean banning the production of all these goods and create a loss for society. The benefit of pollution simply reflects the benefit of these goods. (It is for this reason that market efficiency does not generally mean that the level of a negative externality must be driven to zero.)

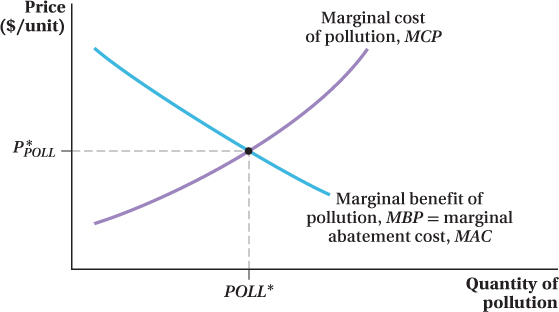
We can see how the efficient level of pollution is determined in Figure 17.3. In reality, it is likely that the marginal cost of pollution (MCP) rises with the level of pollution. The incremental damage of more pollution is relatively modest at low levels, but the severity of the damage grows as pollution increases. This is reflected in the shape of curve MCP in Figure 17.3.

660

The marginal benefit of pollution (MBP), on the other hand, is likely to be high at low levels because some positive level of pollution is necessary to make goods. But, the marginal benefit will tend to fall as pollution output increases (and as output of the good increases). At higher output levels of pollution (and the good), production technologies can become more flexible so that less pollution is produced at higher quantities of the good’s output. Also, because demand curves slope down, the price at which an industry can sell its marginal unit of output falls, which, in turn, makes pollution less valuable on the margin. These factors are reflected in curve MBP in Figure 17.3.

There is a different way to think about the marginal benefit curve MBP that allows us to consider how much it would cost a firm to reduce the level of pollution it creates. Just as the MBP curve shows the marginal benefit from pollution, it also reflects the flip-side: the marginal cost of cutting pollution, also called pollution abatement. After all, every unit of pollution a producer cuts entails a lost marginal benefit: the loss of the sale of the extra product that could have been made using that extra unit of pollution. As more cuts in the amount of pollution are made (i.e., as we move from right to left along the horizontal axis in the figure), the marginal cost of cutting pollution rises. Therefore, MBP also reflects the marginal cost of cutting pollution, which economists often call the marginal abatement cost (MAC). This is shown in Figure 17.3 by indicating that MBP and MAC are equal, allowing us to view this curve in either way.

The efficient level of pollution is where its marginal benefit equals its marginal cost, or POLL* in Figure 17.3. The logic is the same as we’ve seen before: If something’s marginal benefit is higher than its marginal cost, produce more; if its marginal cost is greater than its marginal benefit, produce less. Net benefits are maximized where the next unit equates the two marginal effects.

If we want to think of the marginal benefit curve as being the marginal abatement cost curve instead, we can interpret optimal pollution in terms of emissions cuts. Emissions should be cut whenever the marginal cost of a reduction in the level of emissions (as reflected by the MAC curve) is less than the reduced harm (as reflected by MCP). This will be true at any pollution levels greater than POLL*. On the other hand, if marginal abatement costs are greater than the marginal cost of the pollution, which will be the case at pollution levels less than POLL*, then pollution cuts should be scaled back. These considerations are balanced at the optimal pollution level POLL*.

661

The optimal “price” of pollution is equal to the marginal cost of pollution (and marginal benefit) at the optimal quantity, or P*_POLL in Figure 17.3. If pollution were tradable (which, as we see later, it can be), at P*_POLL polluters would be willing to purchase the right to pollute up to the level POLL*. For levels of pollution below POLL*, the price P*_POLL is lower than the value from being able to pollute more (measured by the marginal benefit of pollution). At the same time, those harmed by pollution would still be willing to sell an amount of pollution rights equal to POLL*, because at this price they are being more than compensated for the harm they suffer (P*_POLL > MCP).

In principle, an efficient level of pollution could result from either price or quantity mechanisms. If regulators could impose the socially optimal price in a market, for instance, the quantity (of either the good or the externality) at that price would also be at its optimal level. Similarly, if regulators could specify the socially optimal quantity, the price at that quantity would be the optimal price. In practice, however, we will see that one approach may be easier than the other to enact, depending on the nature of the externality and the information available to regulators.

One way to view the failure of the free market in the presence of externalities is that the market participants do not consider the correct, society-wide costs and benefits when they make their decisions. If prices can be modified so that the private cost matches the social cost or the private benefit matches the social benefit, then producers and consumers would make the “right” choice, the choice that results in a welfare-maximizing price and quantity.

For goods tied to negative externalities, price-based mechanisms apply additional costs by making firms or consumers pay an extra amount for each unit of the good they produce or consume. This causes them to cut back on production or consumption, bringing down the market quantity toward the efficient level.

For goods associated with positive externalities, additional demand can be added by paying firms for producing (or buyers for purchasing) each unit of output. This, in essence, raises the demand curve faced by the producers, spurring them to increase output. Therefore, the price received by the seller and the amount of output produced will become equal to their efficient levels.

Pigouvian Taxes One of the most common types of price-modification policy used to address negative externalities is a Pigouvian tax.8 This type of tax (named after the British economist Arthur Pigou who pioneered the idea in 1920) raises a good’s price to take into account the external marginal costs imposed by a negative externality.9

Let’s look at how a Pigouvian tax works. Suppose that coal-burning power plants emit pollution that dirties the air of surrounding communities and imposes health costs on the people living in those areas. A Pigouvian tax on electricity generated by these plants would bring equilibrium in the electricity market toward an efficient level of output and price (Figure 17.4).

662

Because the electricity industry’s private marginal costs MC_I are not the same as the social marginal costs SMC, we get overproduction: The power company generates Q_MKT when the optimal quantity is Q*.

Now, let’s say that a government could impose a tax T per MWh on electricity production equal to the external marginal cost EMC of pollution. This would increase the private marginal cost of supplying energy, and shift MC_I up to MC_I + T. Because T = EMC, the industry’s marginal cost curve is now the same as the social marginal cost curve SMC. The old marginal cost curve MC_I intersected the demand curve at the price P_MKT. At that price, the industry’s output was Q_MKT. If the size of the tax is chosen so that the tax-inclusive marginal cost curve MC_I + T intersects the demand curve at the efficient price P*, the industry’s output falls to the efficient quantity Q*.

The Pigouvian tax raises the electricity industry’s marginal cost by an amount equal to the external damages its production causes. This exactly aligns the industry’s private incentives with society’s. In effect, the Pigouvian tax “internalizes” the pollution externality. That is, it forces the industry to take into account the external damage of its operations when it decides how much electricity to generate. This process results in the efficient market outcome.

In reality, there are all kinds of Pigouvian taxes. One of the rationales for placing taxes on cigarettes and alcohol and for the recent calls for imposing taxes on soda arises from the external costs (from second-hand smoke, drunk driving, obesity, health expenses, etc.) that consumers of these goods do not otherwise bear.

Another example of a Pigouvian tax comes from the European Union. A few years ago, the EU proposed curbing greenhouse gas pollution and global warming by imposing a carbon emissions fee on international airline flights. This fee would force the airlines to account for the high amounts of greenhouse gas emissions made by large commercial aircraft. The effectiveness of this fee suffered when several large nations including India and China refused to require their airlines to pay it.

663

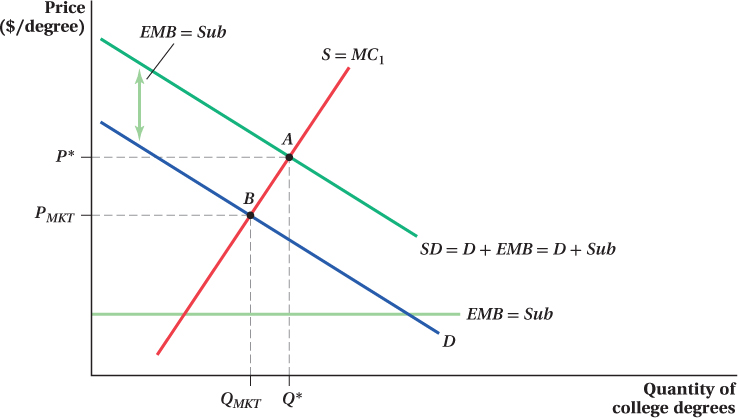
Pigouvian Subsidy When there is a positive externality, a Pigouvian subsidy can be used to decrease a good’s price (paid by the buyer) to take into account the external marginal benefits. The subsidy raises the effective price (the market price plus the subsidy) at which producers can sell their products, thus making it profit-maximizing for them to increase their outputs to the socially optimal level. In the market for college degrees (presented again in Figure 17.5), the private market would produce only Q_MKT degrees if left to its own devices. However, if the government institutes a subsidy of Sub per student (exactly equal to the EMB), the demand for college degrees rises to D + Sub, which also happens to be the social demand curve. Output in the market rises to Q*, the socially optimal level of output.

664

There are many types of actual subsidies that are at least supposed to be based on Pigouvian principles. Tax credits for education or to buy hybrid cars and fuel-efficient home appliances are examples of Pigouvian subsidies.

One practical problem facing Pigouvian taxes and subsidies is how to figure out their correct size. Realistically, it’s difficult to estimate the exact external marginal cost of carbon pollution or the exact external marginal benefit from more college degrees, so setting the correct rate for the Pigouvian tax or subsidy is also difficult. If a government sets the Pigouvian tax or subsidy at the incorrect level, the market price and quantity will still be inefficient. We discuss this problem more below.

665

Quantity-based interventions have the same goal as price-based mechanisms: to move a market with externalities toward the efficient outcome. They just use a different lever.

Quotas The simplest of the quantity-based approaches is to set a quota, a mandated limit on the quantity of a good or an externality a producer can make or a consumer can buy (if the externality is negative), or a required quantity of a good or an externality a producer must make or a consumer must purchase (if the externality is positive). By regulating output, the amount of the externality associated with producing this output is also regulated. With negative externalities, the quantity restriction must be set below the free-market equilibrium quantity, at the lower, socially efficient quantity. Quantity can also be controlled with licensing, where only a particular amount of an activity (production or consumption) is allowed by authorities.

In Figure 17.6, we look once again at the market for electricity production and see that the pollution externality leads to excessive production at Q_MKT and an inefficient market outcome. Suppose that the government enacts a law mandating that the production of electricity can be no greater than Q*. With this law in place, the private MC_I curve becomes vertical at that quantity level. The private MC_I curve now intersects the demand curve at point A and the private decision matches the socially efficient one.

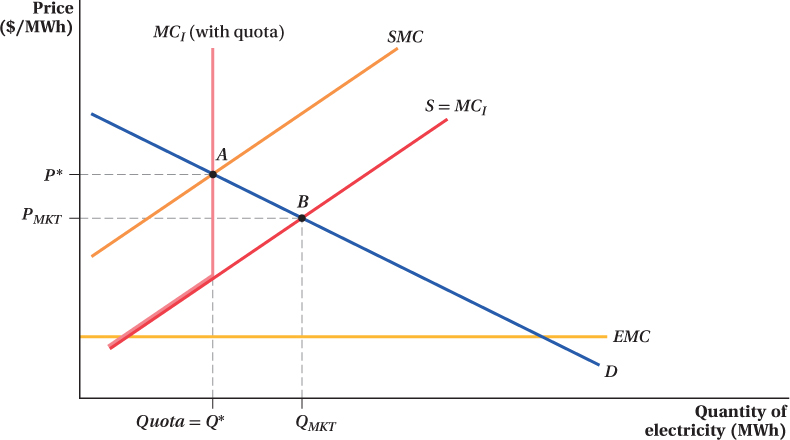
Examples of quotas used in actual practice include restrictions on the amount of pollution factories can emit and the amount of noise neighbors can make. Similarly, hunting and fishing licenses limit the number of fish or animals a person can take because of the negative externality of overfishing and overhunting.

We see fewer real-world mandates for positive externalities. Such quotas require people to supply or purchase a minimum quantity that is higher than the free-market equilibrium output. For example, people are required by law to attend school until age 16 in most states. Vaccines for infectious diseases are often mandated by law, as is the purchase of auto liability insurance for drivers. Each of these is a quantity-based way to promote more of an activity that has a positive externality on others.

667

Practically speaking, however, the use of quotas creates complications. First, as with setting Pigouvian taxes, it is difficult to determine what the socially optimal amount of the quotas actually should be.

A second difficulty with quotas is that the government often wants to influence the total amount of an externality produced by an industry, but can only set quotas on a firm-by-firm basis. For example, it might be much more expensive to reduce pollution emitted from old power plants and much cheaper to reduce pollution from newer plants. Under these conditions, enacting a rule that says each plant must hit the same target level will not be the most cost-effective way to accomplish the goal of less pollution. (In the next section, we discuss how giving out permits and allowing permit holders to buy and sell the permits can solve this complication.)

Third is the question of the distribution of costs and benefits. A Pigouvian tax, for example, generates revenues for the government (or costs the government in the case of subsidies). With quotas and mandates, the benefits or costs are left with the market participants. With licensing, the government receives some revenue, while market participants incur some cost but also reap some benefits.

Government Provision of a Good Another type of quantity intervention in the case of positive externalities occurs when the government actually provides the product itself. Basic scientific research has a large positive externality and little private sponsorship, so the federal government subsidizes it through tax credits and research funding. Governments also perform research directly, as does the United States at the National Institutes of Health and a system of federal labs around the country.

668

We saw above that, as a matter of principle, quantity and price mechanisms can be equally effective at addressing externalities. In reality, though, there are situations in which one type of market intervention might be preferred to the other.

A particularly important situation in which one mechanism might be preferred to the other is when the optimal level of the externality is not fully known. The importance of uncertainty in dealing with externalities was first pointed out by American economist Martin Weitzman in 1974.12

Such uncertainty is common. The marginal benefits and the marginal costs of pollution are difficult to measure and often shift with changes in technologies, input costs, and new discoveries about how damaging pollution is to human health. As a result, efforts to intervene in markets with externalities are generally inexact, so any Pigouvian taxes or quantity mandates that regulators set are not exactly right. Not being exactly right is always costly, but it can be even more costly if the wrong intervention is used.

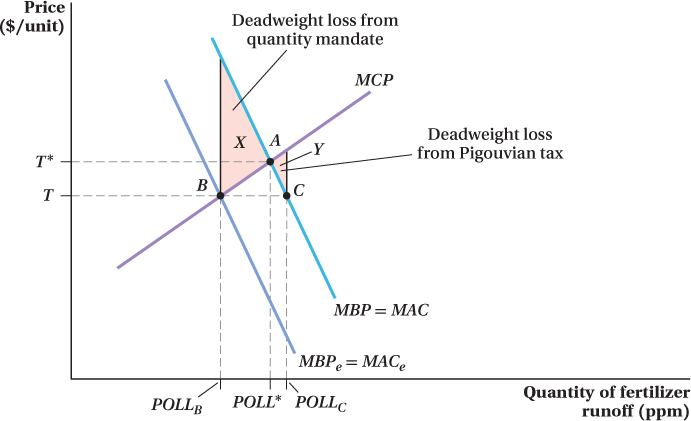
Let’s look at Figure 17.7, which illustrates the marginal cost and marginal benefit of water pollution caused by fertilizer runoff from farms (measured in parts per million, or milligrams per liter of water). The marginal cost of water pollution is shown by the MCP curve. The marginal benefit of pollution and the marginal cost of removing this pollution are shown by the MBP = MAC curve. In Figure 17.7, the efficient quantity of runoff pollution in the market POLL* is found where the marginal benefit of pollution is exactly equal to the marginal cost of pollution (point A).

669

Before we examine how uncertainty can affect the ability of a regulation to move the market to its efficient level of pollution, let’s remind ourselves of how to measure the deadweight loss that occurs when the pollution level is not at the efficient level. The deadweight loss equals the area between the marginal benefit of pollution (alternatively, the marginal abatement costs) and the marginal cost of pollution for each of the units of pollution between the efficient level of pollution and the current level of pollution.

If the level of pollution is too high (to the right of POLL*), pollution costs society more (as seen by the MCP curve) than its value (in terms of output produced along with the pollution, reflected in the MBP curve). Conversely, when the level of pollution is inefficiently low (the level lies to the left of POLL*), there are units of pollution that provide greater value (in terms of the output that would be produced along with the pollution) than their cost.

Now suppose the regulator does not know exactly what farmers’ marginal abatement costs are, and so is unsure about the true marginal benefits of water pollution. Can we say whether the regulator would be better off choosing a quantity- or price-based mechanism to reduce the pollution to its efficient level?

For example, suppose the regulator mistakenly estimates farmers’ marginal abatement costs as being lower than they really are, shown by curve MBP_e = MAC_e in Figure 17.7. If these were the true abatement costs, the optimal level of pollution would be POLL_B because the marginal cost of pollution is equal to the estimated marginal benefit of pollution at point B. The regulator could achieve a pollution level of POLL_B in two ways: by limiting the quantity of fertilizer used so that total runoff pollution is POLL_B, or by setting a tax on runoff at price T.

If the regulator uses a quantity mechanism, the amount of pollution will be limited to POLL_B, lower than the socially optimal level POLL*. In this case, the deadweight loss from incorrectly mandating the quantity is the triangle X in Figure 17.7. This area reflects the pollution for which the true marginal benefit is higher than the marginal cost to society. This pollution does not occur, however, because of the quantity restriction at the wrong pollution level.

If the regulator instead uses a Pigouvian tax equal to T, farmers will reduce their fertilizer use from where it would be without any tax until their marginal abatement cost equals the tax (at point C). Additional cuts in the level of pollution beyond this point would be more expensive (in terms of forgone output) than simply paying the pollution tax. So, this incorrect tax (due to the mis-estimate of marginal abatement costs) results in the farmers polluting an amount, POLL_C, that is much greater than the optimal level. The deadweight loss from this mistake by the regulator is area Y. Comparing area Y (caused by setting the wrong price) to the deadweight loss of area X (caused by setting the wrong quantity), it’s clear that setting the wrong tax creates a much bigger loss, even though both the quantity restriction and tax were not far from their optimal values in absolute terms. Note that the optimal tax level would be T*, which would result in the efficient level of pollution POLL*.

This result—that price-based mechanisms led to larger inefficiency losses—is not a consequence of the regulator believing that abatement costs were lower than they actually were. If the regulator were instead mistaken in the other direction—that is, it thought abatement costs were higher than they really were—we’d find the same thing. (Though in that case, pollution will be above the optimal level under a quantity-based intervention and below it with a Pigouvian tax.)

The reason why the deadweight losses are so much larger with price mechanisms results from the way we set up the example. We’ve drawn the marginal abatement curve as relatively flat and the marginal cost of pollution curve as relatively steep. The flat MAC curve implies that farmers’ abatement choices are very sensitive to the price of abatement (in other words, the tax), so being just a little wrong on setting a Pigouvian tax leads to wild swings in the amount of pollution the farmers create. These large swings, in turn, cause big inefficiency losses because the marginal cost of pollution is so sensitive to the amount of pollution (as shown by the steep MCP curve). Therefore, when faced with cases in which farmers’ abatement choices are sensitive to a tax and the marginal cost of pollution is likely to rise rapidly with pollution, regulators should favor quantity-based interventions. That way, if they’re wrong about how much tweaking the market needs, damages will be limited.

670

If the situation were reversed, and the marginal abatement cost curves were fairly steep and the marginal cost of pollution curve were relatively flat, price mechanisms cause fewer inefficiency losses than quantity-based interventions. This case is shown in Figure 17.8.

In Figure 17.8, the optimal level of pollution from fertilizer runoff is at point A, where the marginal cost of pollution equals the marginal benefit of pollution (or marginal abatement cost), and the efficient level of pollution is POLL*. Once again, suppose the regulator believes that farmers’ abatement costs are lower than they really are, shown by curve MBP_e = MAC_e. If regulators use a quantity-based intervention, they will set the quantity mandate at POLL_B, pollution will be POLL_B instead of POLL*, and area X will be the deadweight loss from inefficiency. If a Pigouvian tax is used instead, regulators will set it at T. Farmers will produce a quantity of pollution POLL_C, and the deadweight loss from the inefficient level of pollution is area Y.

Figure 17.8 shows that when the marginal abatement cost curve is steep relative to the marginal cost of pollution curve, setting incorrect Pigouvian taxes is less costly than setting incorrect quantity mandates. The relative insensitivity of abatement to the level of the tax means that being a little wrong about the optimal tax won’t have much effect on the actual level of pollution. But, setting the wrong quantity will be very costly. Regulations that force producers to undertake unnecessarily high abatement will be expensive relative to the marginal costs of pollution it saves. Similarly, mandating too little abatement will mean that some pollution cuts with benefits that would far outweigh their costs won’t be made.

671

Therefore, when regulators are uncertain about the optimal level of an externality, the choice of quantity- or price-based market interventions should depend on what the regulator perceives are the relative sensitivities of the marginal cost of pollution and the marginal abatement cost (or marginal benefit of pollution).

Trying to mandate the total externality in a market by restricting each firm’s quantity or determining the correct amount to tax involves a lot of effort. Worse, it may lead to costly errors if producers differ in their costs of changing output levels. It would be optimal for firms that could do this more cheaply to make a larger share of the necessary quantity adjustments. But, it can be very difficult for a regulator to know what each firm’s costs are and set quantity restrictions or taxes appropriately.

In these cases, it can be preferable to allow firms to jointly determine how best to reduce an externality to its optimal level. Tradable permits for pollution can achieve this. These are permits issued to firms by the government that allow the holder to emit a certain amount of pollution, and no one can pollute without one. After the permits are allocated among firms, they can be traded, allowing some firms to emit a greater amount of pollution than others. In essence, a market for pollution emissions develops. Such systems are sometimes called “cap-and-trade” programs for this reason: The government sets a cap on pollution emissions, issues an amount of permits equal to this cap, and then firms trade the rights to pollute among them. For example, the United States regulates sulfur dioxide (SO₂) using a system of tradable permits.

A competitive tradable permits market will arrive at a price per permit that equates the marginal cost of pollution abatement across all firms. Suppose the permit price was above a firm’s marginal abatement cost (alternatively, its marginal benefit of polluting). It could then make a profit by reducing its pollution by 1 unit and selling the permit that the marginal unit of pollution would have required. If permit prices were instead below its marginal benefit of pollution, it could raise its profits by buying a permit and polluting an extra unit. Only when the permit price equals the marginal abatement cost of the firm would it not want to change its pollution level. Because this logic holds for every firm, each firm’s level of pollution must equate that firm’s marginal abatement cost to the permit price. (This is similar to the logic in a perfectly competitive market where all firms produce a quantity that equates their marginal cost to the output price.)

This is an important result; it means the total amount of abatement in the industry (as set by the government cap) is done efficiently. If one firm has a lower marginal abatement cost than another, it should reduce pollution more. A permit market ensures that all firms have the same marginal abatement cost, so no reshuffling of pollution reduction across firms would lower the total cost of reducing pollution.

Moreover, if the government sets the total number of permits to the efficient level of pollution, then (by definition of the efficient level) the permit price will equal the marginal benefit of pollution reduction. Therefore, a competitive permit market ends up with each firm cutting pollution to the point where its cost of doing so equals society’s benefit from those cuts.

672

The permit market achieves the total emissions cuts necessary for efficiency at the lowest possible cost, and it does so without the regulator having to determine which firm cuts how much. It works because allowing permit trading lets firms that face lower abatement costs shoulder more of the emissions-cutting burden and be compensated for it by selling their permits. High-abatement-cost firms prefer to buy these permits because it’s cheaper for them than cutting emissions directly.