Producer Behavior 6

Problems

Consider the production function presented in the table below:

Capital (K)		Labor (L)
	0	1	2	3	4	5	6
	1	100	200	300	400	500	600
	2	200	400	600	800	1,000	1,200
	3	300	600	900	1,200	1,500	1,800
	4	400	800	1,200	1,600	2,000	2,400
	5	500	1,000	1,500	2,000	2,500	3,000
	6	600	1,200	1,800	2,400	3,000	3,600

If the firm decides to employ 6 units of capital and 1 worker, what is its output?

The firm’s output is 600.
What other combinations of capital and labor could be used to produce the same level of output you found in (a)?

Output of 600 can also be achieved with either 3 units of capital and 2 units of labor, 2 units of capital and 3 units of labor, or 1 unit of capital and 6 units of labor.
Plot the combinations you determined in (a) and (b) on a graph, with labor on the horizontal axis and capital on the vertical axis. Connect the dots to form the production isoquant corresponding to 600 units of output.

The table below represents the production function for Hawg Wild, a small catering company specializing in barbecued pork. The numbers in the cells represent the number of customers that can be served with various combinations of labor and capital.

Capital (K)		Labor (L)
	0	1	2	3	4	5	6
	1	100	132	155	174	190	205
	2	152	200	235	264	289	310
	3	193	255	300	337	368	396
	4	230	303	357	400	437	470
	5	263	347	408	457	500	538
	6	293	387	455	510	558	600

Is this production function a short-run or long-run production function? How can you tell?
Suppose that Hawg Wild employs 5 units of capital and 2 workers. How many diners will be served?
Suppose that Hawg Wild employs 5 units of capital and 2 workers, but that the owner, Billy Porcine, is considering adding his nephew to the payroll. What will the marginal product of Billy’s nephew be?

234
Notice that when Hawg Wild uses 1 unit of capital, the marginal product of the fifth unit of labor is 16. But when Hawg Wild uses 5 units of capital, the marginal product of the fifth unit of labor is 43. Does this production function violate the law of diminishing marginal product of labor? Why or why not?
Suppose that Hawg Wild employs 5 units of capital and 2 workers, but that the owner, Billy Porcine, is considering adding another meat smoker to the kitchen (which will raise the amount of capital input to 6 units). What will the marginal product of the smoker be?
Hawg Wild employs 5 units of capital and 2 workers. Billy is considering the choice between hiring another worker or buying another smoker. If smokers cost $8 and workers $12, then at the margin, what is the most cost-effective choice for Billy to make?

Complete the table below:

Labor Input Total Product Marginal Product Average Product

0 0 — —

1 70

2 135

3 63

4 51

5 57

6 324
Jerusha, a woodworker, builds coffee tables using both labor (L) and tools (capital, or K). Her production function for coffee tables is a Cobb–Douglas production function: Q = 4K^.5L^.5.
1. Can Jerusha build any coffee tables without tools?
2. Can Jerusha completely mechanize coffee table production?
3. Jerusha currently has 16 tools, and in the short run can neither acquire more tools nor sell existing tools. Her woodshop is capable of holding up to 49 employees. What is Jerusha’s short-run production function?
4. Graph the production function you found in (c), with labor on the horizontal axis and output on the vertical axis. (Hint: Don’t plot every possible amount of labor; instead, choose convenient levels of L that are perfect squares: 0, 1, 4, 9, etc.)
5. Determine the average and marginal products of labor at each level of labor you worked with in (d). (Hint: To compute the marginal product of the 25th worker, you’ll need to figure out how much Jerusha would produce with both 25 and 26 workers.)
6. Suppose that overnight, 7 of Jerusha’s machines fail. Show what happens to the total, marginal, and average products of labor as a result.
Abel, Baker, and Charlie all run competing bakeries, where each makes loaves of bread.
1. At Abel’s bakery, the marginal product of labor is 15 and the average product of labor is 12. Would Abel’s average product increase or decrease if he hired another worker?
2. At Baker’s bakery, the marginal product of labor is 7 and the average product of labor is 12. Would Baker’s average product increase or decrease if he hired another worker?
3. At Charlie’s bakery, the MPL is –12. Does this mean her average product must also be negative?
4. Based on your answers above, can you generalize the nature of the relationship between the average and marginal products of labor?
Work this problem with calculus

Suppose that a firm’s production function is given by Q = K^0.33L^0.67, where MP_K = 0.33K^–0.67L^0.67 and MP_L = 0.67K^0.33L^–0.33.
1. As L increases, what happens to the marginal product of labor?
2. As K increases, what happens to the marginal product of labor?
3. Why would the MP_L change as K changes?
4. What happens to the marginal product of capital as K increases? As L increases?
Fetzer valves can be made in either China or the United States, but because labor in the United States is more skilled, on average, than labor in China, the production technologies differ. Consider the two production isoquants in the figure below. Each represents either the production technology for the United States or for China. Based on the MRTS, which production isoquant is more likely to represent the United States and which represents China? Explain.

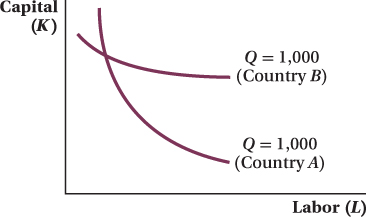
235
Work this problem with calculus

Solution

Consider the production functions given below:
1. Suppose that the production function faced by a 30-weight ball bearing producer is given by Q = 4K^0.5L^0.5, where MP_K = 2K^–0.5L^0.5 and MP_L = 2K^0.5L^–0.5. Do both labor and capital display diminishing marginal products? Find the marginal rate of technical substitution for this production function. (Hint: The MRTS = MP_L/MP_K.) Does this production function display a diminishing marginal rate of substitution?
  
  The marginal product of capital will decrease as capital increases, and the marginal product of labor will decrease as labor increases. Thus, they both exhibit diminishing marginal products. The MRTS is
  
  (2K^0.5L^–0.5)/(2K^–0.5L^0.5) = K/L
  
  As labor increases, this value will diminish. Therefore, the marginal rate of substitution is diminishing.
2. Suppose that the production function faced by a 40-weight ball bearing producer is given by Q = 4KL, where MP_K = 4L and MP_L = 4K. Do both labor and capital display diminishing marginal products? Find the marginal rate of technical substitution for this production function. Does this production function display a diminishing marginal rate of substitution?
  
  For a given amount of labor, the marginal product of capital is constant. For a given amount of capital, the marginal product of labor is constant. Hence, neither input exhibits diminishing marginal returns. The MRTS is
  
  4K/4L = K/L
  
  As labor increases, the MRTS will diminish.
3. Compare your answers to (a) and (b). Must labor and capital display diminishing marginal products in order for the MRTS to diminish?
  
  In both (a) and (b), the production function displays a diminishing MRTS. Yet in (b), both inputs were characterized by a constant marginal product. So a diminishing rate of substitution can be found even when marginal product is not diminishing.
Suppose that Manny, Jack, and Moe can hire workers for $12 per hour, or can rent capital for $7 per hour.
1. Write an expression for Manny, Jack, and Moe’s total cost as a function of how many workers they hire and how much capital they employ.
  
  The cost function is
  
  $12 × L + $7 × K
2. Assume that Manny, Jack, and Moe wish to hold their total costs to exactly $100. Use your answer from (a) to find the equation for an isocost line corresponding to exactly $100 of costs. Rearrange your equation to isolate capital.
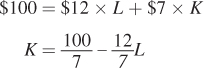
3. Graph the equation for the isocost line, putting labor on the horizontal axis and capital on the vertical axis.
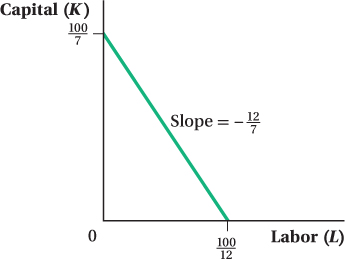
4. What is the vertical intercept of the line you drew? The horizontal intercept? What does each represent?
  
  The vertical intercept indicates the quantity of capital that can be rented with $100 if no labor is hired. The horizontal intercept indicates the quantity of labor that can be hired with $100 if no capital is rented.
5. What is the slope of the line you drew? What does it represent?
  
  The slope is the (negative) ratio of the price of labor (wage) and the rental price of capital. The isocost line has a slope of .
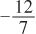6. Suppose that bargaining with the local labor union raises wages. Manny, Jack, and Moe must now pay $14 per hour. What happens to the isocost line corresponding to $100 of expenditure? Explain. Show the new isocost line on your graph.
  
  In this case, the isocost function rotates inward as shown:
  
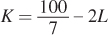
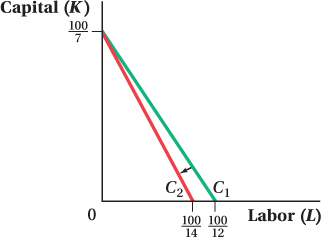
  The new isocost line is steeper; the slope is –2.
A jeweler can potentially use two inputs in her handcrafted jewelry: copper or bronze. She finds that when she minimizes her costs, she uses either copper or bronze, but never both. What must her isoquants look like? What does this suggest about the relationship between copper and bronze?
Work this problem with calculus

Miguel and Jake run a paper company. Each week they need to produce 1,000 reams of paper to ship to their customers. The paper plant’s long-run production function is Q = 4K^0.75L^0.25, where Q is the number of reams produced, K is the quantity of capital rented, and L is the quantity of labor hired. For this production function, the MP_L = K^0.75/L^0.75 and the MP_K = 3L^0.25/K^0.25. The weekly cost function for the paper plant is C = 10K + 2L, where C is the total weekly cost.
1. What ratio of capital to labor minimizes Miguel and Jake’s total costs?
2. How much capital and labor will Miguel and Jake need to rent and hire in order to produce 1,000 reams of paper each week?
3. How much will hiring these inputs cost them?
Baldor, Inc. measures the marginal rate of technical substitution (MRTS) at MP_L/MP_K = 3. The prices of labor and capital faced by Baldor are such that currently W/R = 4.
1. Is Baldor minimizing its costs?
2. What can Baldor do to improve its situation?
Suppose that the production function for iPhones is Q = 20K^0.5L^0.5. The marginal product of labor is 10(K/L)^0.5, and the marginal product of capital is 10(L/K)^0.5.
1. Suppose that labor can be hired for $6, and capital can be hired for $9. When the firm is producing 49 units at lowest cost, what will the firm’s marginal rate of technical substitution be?
  
  The firm’s marginal rate of technical substitution is
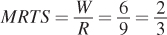
2. Solve for the lowest-cost combination of labor and capital that will allow the firm to produce 49 iPhones. Fractional units of labor and capital are permissible.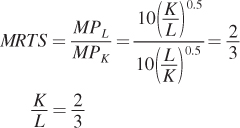
  
  Using the production function, we get
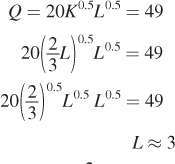
3. What is the minimum cost of producing 49 iPhones?
  
  The minimum cost of producing 49 iPhones is
  
  $6 × 3 + $9 × 2 = $36
4. Suppose that the firm has exactly $300 to spend on producing iPhones. What is the maximum number of iPhones it can produce?
  
  From the cost function
  
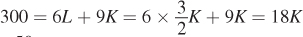
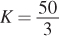  . Hence,
  
  L = 25
  
  Thus, the maximum number of iPhones it can produce is
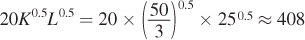
236
Work this problem with calculus

A young college student on a tight budget is campaigning for an open city council seat. A friend in her economics class estimates that voters are influenced by TV and newspaper ads according to the following function: Votes = 300TV^0.6NP^0.2, where TV represents the number of television ads and NP represents the number of newspaper ads. Thus, the marginal product of a newspaper ad is 60TV^0.6NP^–0.8 and the marginal product of a TV ad is 180TV^–0.4NP^0.2. A local television ad costs $400, and a local newspaper ad costs $250. If the candidate needs 1,800 votes to win, what is the lowest-cost combination of newspaper and TV ads that will bring her victory?
Mad Max’s Road Warriors fix potholes in interstate highways. Max’s road crews fill potholes using workers and shovels in 1 to 1 correspondence. A worker with 1 shovel can fill 10 potholes in a day. A worker with 2 shovels can still only fill 10 potholes, as can 2 workers with 1 shovel.
1. Draw the production isoquant corresponding to filling 30 potholes.
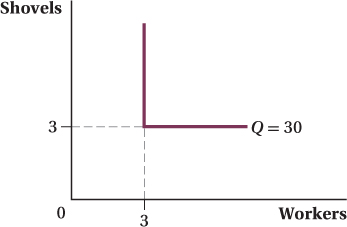
2. Assume that production displays constant returns to scale, and draw a few more isoquants.
3. If shovels rent for $5, and workers must be paid $25, draw several isocost lines.
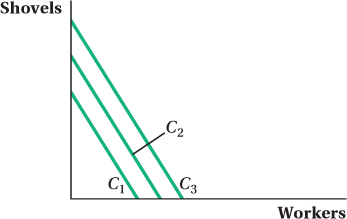
4. If Mad Max has received a state contract to fill 30 potholes, what is the minimum cost at which it can fulfill the contract?
  
  The minimum cost at which Mad Max can fulfill the contract is
  
  3 × $5 + 3 × $25 = $90
5. If the cost of renting a shovel suddenly rises from $5 to $6, what will happen to the composition of inputs that Mad Max uses to fill potholes? Why?
  
  The composition of inputs will not change as Mad Max still needs to have an equal number of workers and shovels.
Use a diagram with one ordinary production isoquant and various isocost lines to show that a firm’s cost of producing a given level of output in the long run will always be less than or equal to its cost of producing that same level of output in the short run. (Hint: To represent the short run, fix capital at one level, K₁. To do this, simply erase the portion of the isoquant that corresponds to capital levels higher than K₁.) Explain intuitively why this must be the case.
Determine whether each of the production functions below displays constant, increasing, or decreasing returns to scale:
1. Q = 10K^0.75L^0.25
2. Q = (K^0.75L^0.25)²
3. Q = K^0.75L^0.75
4. Q = K^0.25L^0.25
5. Q = K + L + KL
6. Q = 2K² + 3L²
7. Q = KL
8. Q = min(3K, 2L)
The graph below illustrates production isoquants for various levels of labor and capital. In the graph, supply the quantities Q₁, Q₂, and Q₃ so that the production function displays
1. Increasing returns to scale
2. Decreasing returns to scale
3. Constant returns to scale
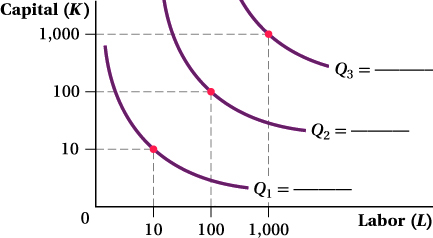
True or false: A production function that displays increasing returns to scale must also display increasing marginal returns to either labor or capital. Explain your answer and provide an example that supports your explanation.
Suppose that the production function for Alfredo Barbuda, a producer of fine violins, is given by the following: Q = 10K^0.5L^0.5.
1. Suppose that Alfredo is currently using 1 unit of capital. If he hires 4 workers, how many violins will they produce?
  
  With 1 unit of capital and 4 units of labor, Alfredo produces
  
  10K^0.5L^0.5 = 10 × 1 × 2 = 20
2. Suppose that Alfredo is currently using not 1, but 2 units of capital. How many workers must he hire to match the level of production you found in (a)?
  
  With 2 units of capital,
  
  20 = 10 × 2^0.5L^0.5
  
  L = 2
  
  Thus, Alfredo must hire 2 workers.
3. Rework your answer to (b), assuming that Alfredo is currently using 4 units of capital.
  
  With 4 units of capital,
  
  20 = 10 × 4^0.5L^0.5
  
  L = 1
  
  SB-11
  
  Thus, Alfredo must hire 1 worker.
4. Plot the combinations of labor and capital you found in (a–c) as a production isoquant.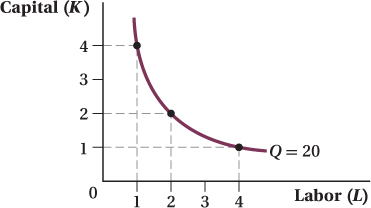
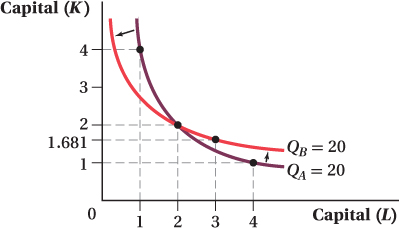
5. (A test of your math skills) A change in capital technology alters Alfredo’s production function. Now Alfredo’s output is given by Q = 10K^0.7L^0.3. If Alfredo employs 3 workers, how many machines will he have to use to achieve the production level you found in (a)? What happens to the isoquant you drew?
  
  The new production function is
  
  10K^0.7L^0.3
  
  To achieve the same level of production with 3 workers,
  
  20 = 10K^0.73^0.3
  
  K ≈ 1.681
  
  The isoquant curve becomes more flat since, to maintain the level of production, more labor is required to substitute 1 unit of capital.
237
Cam’s Cannolis produces delicious desserts. Cam’s production function is depicted by the isoquants in the graph below. If labor and capital are both priced at $10 per unit,
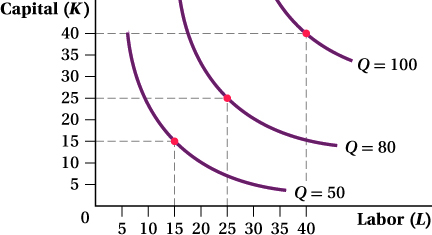
1. Add appropriately sloped isocost lines to the graph to determine the combination of labor and capital that minimizes the cost of producing each level of output shown in the graph.
2. Trace Cam’s expansion path.
3. Determine the total cost of producing each level of output shown in the graph.
4. Create a new graph of Cam’s total cost function, plotting output on the horizontal axis and total cost on the vertical axis.

Labor Input	Total Product	Marginal Product	Average Product
0	0	—	—
1		70
2	135
3			63
4		51
5			57
6	324