Long-run economic growth depends almost entirely on one ingredient: rising productivity. However, a number of factors affect the growth of productivity. Let’s look first at why productivity is the key ingredient and then examine what affects it.

Sustained economic growth occurs only when the amount of output produced by the average worker increases steadily. The terms labour productivity, or Average Productivity of Labour (AP_L) or simply productivity for short, are used to refer either to output per worker or, in some cases, to output per hour. (The number of hours worked by an average worker differs to some extent across countries, although this isn’t an important factor in the difference between living standards in, say, India and Canada.) In this book we’ll focus on output per worker. For the economy as a whole, productivity—output per worker—is simply real GDP divided by the number of people working.

You might wonder why we say that higher productivity is the only source of long-run growth. Can’t an economy also increase its real GDP per capita by putting more of the population to work? The answer is, yes, but …. For short periods of time, an economy can experience a burst of growth in output per capita by putting a higher percentage of the population to work. That happened in Canada during World War II, when hundreds of thousands of women who previously worked only in the home entered the paid workforce. The percentage of adult civilians employed outside the home rose from 51% in 1939 to 61% in 1944, and you can see the resulting bump in real GDP per capita for Canada during those years in Figure 9-1.

Over the longer run, however, the rate of employment growth is never very different from the rate of population growth. Over the course of the twentieth century, for example, Canada’s population rose at an average rate of about 1.7% per year and employment rose by 2.1% per year. Real GDP per capita rose 2.0% per year; of that, 1.6%—that is, about 80% of the total—was the result of rising productivity. In general, overall real GDP can grow because of population growth; a higher population increases the number of workers employed, which in turns raises the real amount of goods and services produced. But any large increase in real GDP per capita must be the result of increased output per worker, that is, it must be due to higher productivity.³

So increased productivity is the key to long-run economic growth. But what leads to higher productivity?

There are three main reasons why the average Canadian worker today produces far more than his or her counterpart a century ago. First, on average, each modern worker has far more physical capital, such as machinery and office space, to work with. Second, the modern worker is much better educated and so possesses much more human capital. Finally, modern firms have the advantage of a century’s accumulation of technical advancements reflecting a great deal of technological progress.

Let’s look at each of these factors in turn.

Increase in Physical Capital Economists define physical capital as manufactured resources such as buildings and machines. Physical capital makes workers more productive. For example, a farmworker operating a tractor can cultivate a lot more farmland per day than one equipped only with a shovel.

The average Canadian private-sector worker today is backed up by more than $190 000 worth of non-residential physical capital—far more than a Canadian worker had 100 years ago and far more than the average worker in most other countries has today.

Increase in Human Capital It’s not enough for a worker to have good equipment—he or she must also know what to do with it. Human capital refers to the improvement in labour created by the education and knowledge embodied in the workforce.

Canada’s human capital has increased dramatically over the past century. A hundred years ago, most Canadians could read and write, but few had an extensive education. In 1920, only 3.2% of Canadians under the age of 25 were enrolled in university or college and about 3% of Canadians between 25 and 29 had a post-secondary degree. By way of contrast, far more people have a post-secondary education today. In 2009, 88% of Canadians aged 25–64 had a high school education and 55% had a college or university education—it would be impossible to run today’s economy with a population as poorly educated as that of a century ago.

Analyses based on growth accounting, described later in this chapter, suggest that education—and its effect on productivity—is an even more important determinant of growth than increases in physical capital.

Technological Progress Probably the most important driver of productivity growth is technological progress, which is broadly defined as an advance in the technical means of the production of goods and services. We’ll see shortly how economists measure the impact of technology on growth.

Workers today are able to produce more than those in the past, even with the same amount of physical and human capital, because technology has advanced over time. It’s important to realize that economically important technological progress need not be flashy or rely on cutting-edge science. Historians have noted that past economic growth has been driven not only by major inventions, such as the railroad or the semiconductor chip, but also by thousands of modest innovations, such as the green plastic garbage bag, invented in Canada in 1950, which made collecting garbage easier, and the egg carton, invented in British Columbia in 1911, which allowed eggs to be delivered unbroken. Experts attribute much of the productivity surge that took place in Canada late in the twentieth century to new technology adopted by retail companies like Loblaws and by cultural services firms such as publishers and broadcasters rather than to high-technology companies.

Aggregate real output for an economy is higher, other things equal, when i) more physical capital is used, ii) more labour (workers) is used, iii) more human capital is used, and/or iv) the technology improves. Economists use the aggregate production function to demonstrate this relation:

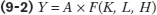
where

This equation shows that if total factor productivity rises, then aggregate real output will also rise, all else the same⁴—a result that can be interpreted as an improvement in technology. We assume that a small increase in K, holding all other inputs and technology fixed, causes the amount of aggregate real output to rise by a marginal amount, called the positive marginal productivity of physical capital (positive MP_K). We also assume that the marginal products of labour and human capital are both positive. If total factor productivity is held constant, then the production function F(…) shows how generous the technology is in increasing productivity, that is, how the technology magnifies the effect of inputs K, L, and H into aggregate real output. Similarly, if the levels of the inputs and the aggregate production remain fixed, then increases in total factor productivity can be interpreted as improvements in technology, since this allows for higher levels of real output to be produced without having to use more inputs.

Likewise, productivity is higher, all else the same, when i) more physical capital is used, ii) human capital increases, and/or iii) the technology improves. In this case we assume that an increase in physical capital per worker causes a rise in real output per worker and that the same holds true for an increase in human capital per worker. So, when total factor productivity rises, then the real output per worker will rise. To quantify these effects, economists use the per worker production function, which shows how productivity depends on the quantities of physical capital per worker and human capital per worker as well as the state of technology:

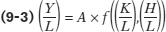
where

In general, all three factors on the right side of the function tend to rise over time, as workers, for example, are equipped with more machinery, receive more education, and benefit from technological advances. What the per worker production function does is allow economists to disentangle the effects of these three factors on overall productivity.

An example of a per worker production function applied to real data comes from a comparative study of Chinese and Indian economic growth by the economists Barry Bosworth and Susan Collins of the Brookings Institution. They used the following aggregate production function:

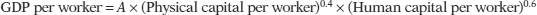
where A represents an estimate of the level of technology and they assumed that each year of education raises workers’ human capital by 7%. Using this function, they tried to explain why China grew faster than India between 1978 and 2004. About half the difference, they found, was due to China’s higher levels of investment spending, which raised its level of physical capital per worker faster than India’s. The other half was due to faster Chinese technological progress (growth in A).

In analyzing historical economic growth, economists have discovered a crucial fact about the estimated per worker production function: it exhibits diminishing returns to physical capital. This is often called diminishing marginal productivity of (physical) capital (dimMP_K). So when the amount of human capital per worker and the state of technology are held fixed, each successive increase in the amount of physical capital per worker leads to a smaller increase in productivity. The graph and table in Figure 9-4 give a hypothetical example of how the level of physical capital per worker might affect the level of real GDP per worker, holding human capital per worker and the state of technology fixed. In this example, we measure the quantity of physical capital in dollars.

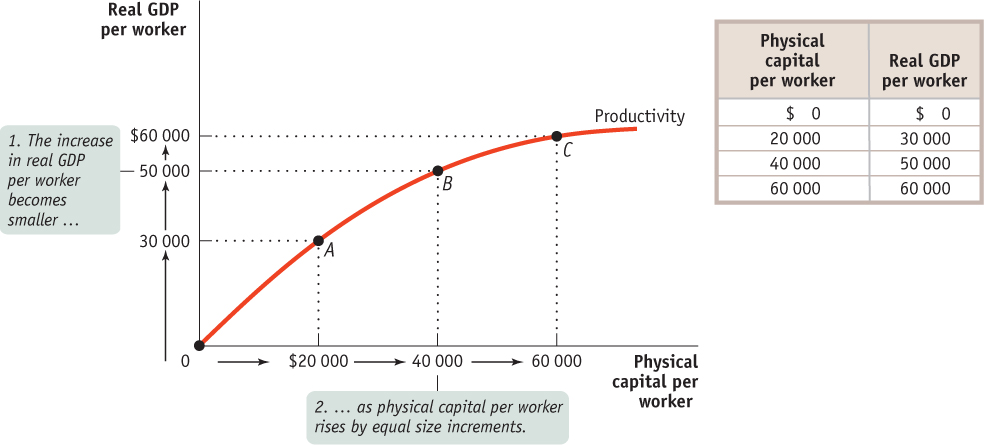
To see why the relationship between physical capital per worker and productivity exhibits diminishing returns, think about how having farm equipment affects the productivity of farmworkers. A little bit of equipment makes a big difference: a worker equipped with a tractor can do much more than a worker without one. And a worker using more expensive equipment will, other things equal, be more productive: a worker with a $40 000 tractor will normally be able to cultivate more farmland in a given amount of time than a worker with a $20 000 tractor because the more expensive machine will be more powerful, perform more tasks, or both.

But will a worker with a $40 000 tractor, holding human capital and technology constant, be twice as productive as a worker with a $20 000 tractor? Probably not: there’s a huge difference between not having a tractor at all and having even an inexpensive tractor; there’s much less difference between having an inexpensive tractor and having a better tractor. And we can be sure that a worker with a $200 000 tractor won’t be 10 times as productive: a tractor can be improved only so much. Because the same is true of other kinds of equipment, the per worker production function shows diminishing returns to physical capital.

Diminishing returns to physical capital imply a relationship between physical capital per worker and real output per worker like the one shown in Figure 9-4. As the productivity curve for physical capital per worker and the accompanying table illustrate, more physical capital per worker leads to more output per worker. But each $20 000 increment in physical capital per worker adds less to productivity. As you can see from the table, there is a big payoff for the first $20 000 of physical capital: real GDP per worker rises by $30 000. The second $20 000 of physical capital also raises productivity, but not by as much: real GDP per worker goes up by only $20 000. The third $20 000 of physical capital raises real GDP per worker by only $10 000. By comparing points along the curve you can also see that as physical capital per worker rises, output per worker also rises (positive MP_K, as shown by an upward slope)—but at a diminishing rate (diminishing MP_K, as shown by a decreasing slope as (K/L) rises). Going from the origin at 0 to point A, a $20 000 increase in physical capital per worker, leads to an increase of $30 000 in real GDP per worker. Going from point A to point B, a second $20 000 increase in physical capital per worker, leads to an increase of only $20 000 in real GDP per worker. And from point B to point C, a $20 000 increase in physical capital per worker increased real GDP per worker by only $10 000.

It’s important to realize that diminishing returns to physical capital is an “other things equal” phenomenon: additional amounts of physical capital are less productive when the amount of human capital per worker and the technology are held fixed.⁵ Diminishing returns may disappear if we increase the amount of human capital per worker, or improve the technology, or both at the same time the amount of physical capital per worker is increased.

For example, a worker with a $40 000 tractor who has also been trained in the most advanced cultivation techniques may in fact be more than twice as productive as a worker with only a $20 000 tractor and no additional human capital. But diminishing returns to any one input—regardless of whether it is physical capital, human capital, or number of workers—is a pervasive characteristic of production. Typical estimates suggest that in practice a 1% increase in the quantity of physical capital per worker increases output per worker by only one-third of 1%, or 0.33%.

In practice, all the factors contributing to higher productivity rise during the course of economic growth: both physical capital and human capital per worker increase, and technology advances as well. To disentangle the effects of these factors, economists use growth accounting, which estimates the contribution of each major factor in the per worker production function to economic growth. Growth accounting can be applied to either the aggregate or the per worker versions of the production function. Growth accounting decomposes the growth rate of output per worker into estimated portions that are the results of the growth rates of physical capital per worker, human capital per worker, and total factor productivity owing to technology. For example, suppose the following are true:

In that case, we would estimate that growing physical capital per worker is responsible for 3% × 0.33 = 1 percentage point of productivity growth per year. A similar but more complex procedure is used to estimate the effects of growing human capital. The procedure is more complex because there aren’t simple dollar measures of the quantity of human capital.

Growth accounting allows us to calculate the effects of greater physical and human capital on economic growth. But how can we estimate the effects of technological progress? We do so by estimating what is left over after the effects of physical and human capital have been taken into account. For example, let’s imagine that there was no increase in human capital per worker so that we can focus on changes in physical capital and in technology.

In Figure 9-5, the lower curve shows the same hypothetical relationship between physical capital per worker and output per worker shown in Figure 9-4. Let’s assume that this was the relationship given the technology available in 1940. The upper curve also shows a relationship between physical capital per worker and productivity, but this time given the technology available in 2010. (We’ve chosen a 70-year stretch to allow us to use the Rule of 70.) The 2010 curve is shifted up compared to the 1940 curve because technologies developed over the previous 70 years make it possible to produce more output for a given amount of physical capital per worker than was possible with the technology available in 1940. (Note that the two curves are measured in constant dollars.)

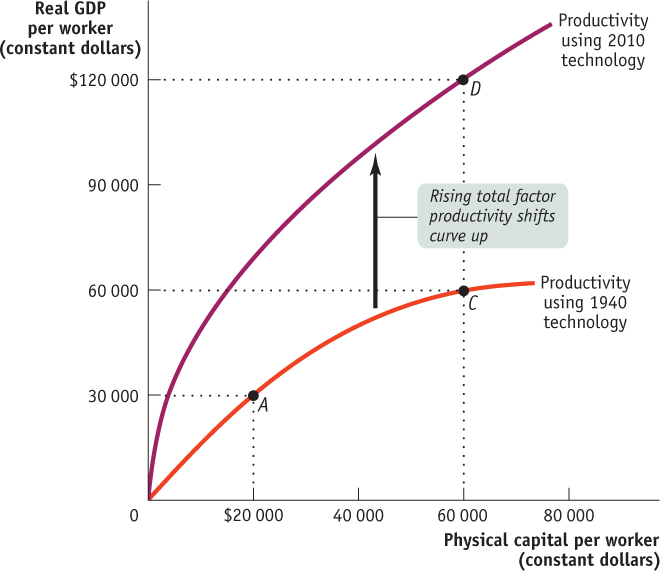
Let’s assume that between 1940 and 2010 the amount of physical capital per worker rose from $20 000 to $60 000. If this increase in physical capital per worker had taken place without any technological progress, the economy would have moved from A to C: output per worker would have risen, but only from $30 000 to $60 000, or 1% per year (using the Rule of 70 tells us that a 1% growth rate over 70 years doubles output). In fact, however, the economy moved from A to D: output rose from $30 000 to $120 000, or 2% per year. There was an increase in both physical capital per worker and technological progress, which shifted the per worker production function.

In this case, 50% of the annual 2% increase in productivity—that is, 1% in annual productivity growth—is due to higher total factor productivity, which here accounts for any additional output per worker produced that did not come from changes in inputs. So when total factor productivity (A) increases, the economy can produce more output with the same quantity of physical capital, human capital, and labour.

Most estimates find that increases in total factor productivity are central to a country’s economic growth in the long-run. Economists believe that, on average, observed increases in total factor productivity do measure the economic effects of technological progress. All of this implies that technological change is crucial to long-run economic growth. Statistics Canada estimates the growth rate of both labour productivity and total factor productivity for various business sectors of Canada. According to estimates from Statistics Canada, from 1961 to 2010 Canadian labour productivity rose 2% per year. Only 57% of that rise is explained by increases in physical and human capital per worker; the rest is explained by rising total factor productivity—that is, by technological progress.

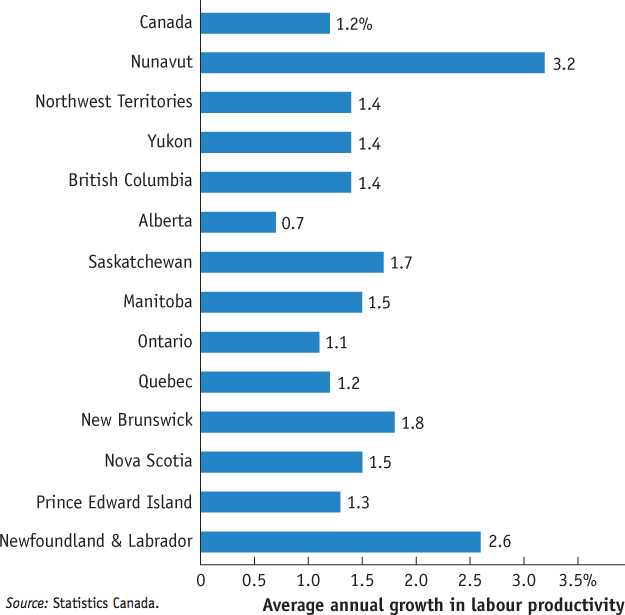
Figure 9-6 shows the average annual growth in labour productivity for all provinces and territories up to 2011. The average labour productivity growth was 1.2% for Canada as a whole. All regions experienced positive labour productivity growth during this period, but the amount of growth varied significantly. Nunavut enjoyed the highest growth rate, with an annual growth rate of 3.2%. Newfoundland and Labrador had the second highest growth with an annual growth rate of 2.6%. On the other hand, Alberta had the lowest labour productivity growth, at 0.7%. You may find this surprising, given the significant amount of industry in Alberta. So why is that province’s annual growth rate so low?

According to Statistics Canada, the answer lies in the rate of accumulation of productive capital or stock of physical capital and total factor productivity growth. During the time frame in question, all regions saw an increase in their physical capital. In fact, Alberta’s (and Saskatchewan’s) physical capital increased by much more than that of the other regions. This is to be expected, because these two provinces are engaged in projects, such as the Alberta oil sands, that are extremely capital-intensive. But the effect of increased physical capital intensity on labour productivity was offset because Alberta and Saskatchewan had negative total factor productivity growth. This negative growth might be attributed to the fact that it requires more effort to produce the same amount of oil from the oil sands as from an oil well. In contrast, in Newfoundland and Labrador, the total factor productivity growth was primarily a result of the province moving toward high productivity economic activity, such as onshore and offshore oil production.

Some regions grew faster while some grew more slowly. But whether the growth is fast or slow, the bottom line is that higher labour productivity transforms into and reflects higher (per capita) economic growth.

In our discussion so far, we haven’t mentioned natural resources, which certainly have an effect on productivity. Other things equal, countries that are abundant in valuable natural resources, such as highly fertile land or rich mineral deposits, have higher real GDP per capita than less fortunate countries. The most obvious modern example is the Middle East, where enormous oil deposits have made a few sparsely populated countries very rich. For example, Kuwait has about the same level of real GDP per capita as Germany, but Kuwait’s wealth is based on oil, not manufacturing, the source of Germany’s high real output per worker.

But other things are often not equal. In the modern world, natural resources are a much less important determinant of productivity than human or physical capital for the great majority of countries. For example, some nations with very high real GDP per capita, such as Japan, have very few natural resources. Some resource-rich nations, such as Nigeria (which has sizable oil deposits), are very poor.

Historically, natural resources played a much more prominent role in determining productivity. In the nineteenth century, the countries with the highest real GDP per capita were those abundant in rich farmland and mineral deposits: Canada, the United States, Argentina, and Australia. As a consequence, natural resources figured prominently in the development of economic thought. In a famous book published in 1798, An Essay on the Principle of Population, the English economist Thomas Malthus made the fixed quantity of land in the world the basis of a pessimistic prediction about future productivity. As population grew, he pointed out, the amount of land per worker would decline. And this, other things equal, would cause productivity to fall.

His view, in fact, was that improvements in technology or increases in physical capital would lead only to temporary improvements in productivity because they would always be offset by the pressure of rising population and more workers on the supply of land. In the long run, he concluded, the great majority of people were condemned to living on the edge of starvation. Only then would death rates be high enough and birth rates low enough to prevent rapid population growth from outstripping productivity growth.

It hasn’t turned out that way, although many historians believe that Malthus’s prediction of falling or stagnant productivity was valid for much of human history. Population pressure probably did prevent large productivity increases until the eighteenth century. But in the time since Malthus wrote his book, any negative effects on productivity from population growth have been far outweighed by other, positive factors—advances in technology, increases in human and physical capital, and the opening up of enormous amounts of cultivatable land in the New World.

It remains true, however, that we live on a finite planet, with limited supplies of resources such as oil and limited ability to absorb environmental damage. We address the concerns these limitations pose for economic growth in the final section of this chapter.