11.1 Using the F Distributions with Three or More Samples
The talking-
Type I Errors When Making Three or More Comparisons
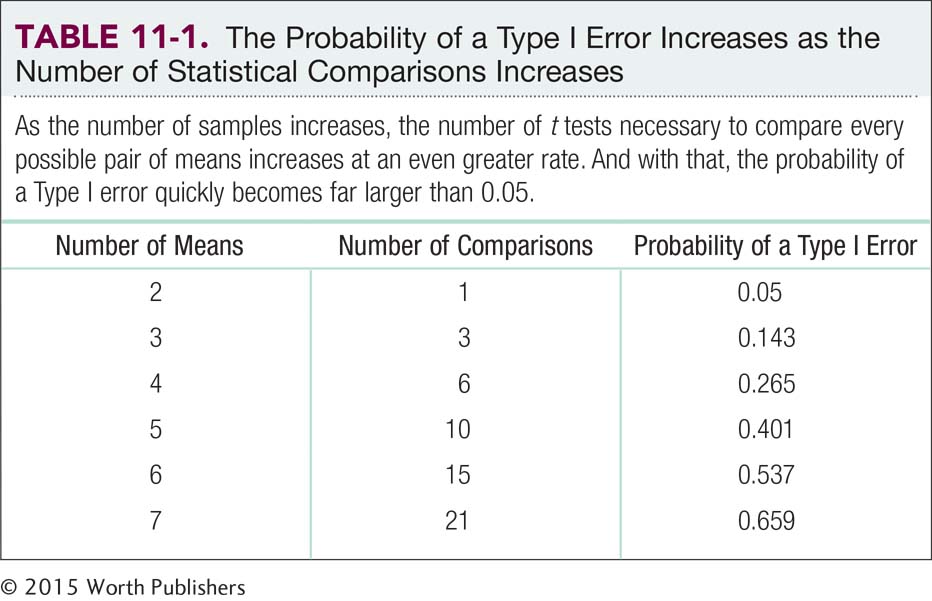
When comparing three or more groups, it is tempting to conduct an easy-
Group 1 with group 2
Group 1 with group 3
Group 2 with group 3
That’s 3 comparisons. If there were four groups, there would be 6 comparisons. With five groups, there would be 10 comparisons, and so on. With only 1 comparison, there is a 0.05 chance of having a Type I error in any given analysis if the null hypothesis is true, and a 0.95 chance of not having a Type I error when the null hypothesis is true. Those are pretty good odds, and we would tend to believe the conclusions in that study. However, Table 11-1 shows what happens when we conduct more studies on the same sample. The chances of not having a Type I error on the first analysis and not having a Type I error on the second analysis are (0.95)(0.95) = (0.95)2 = 0.903, or about 90%. This means that the chance of having a Type I error is almost 10%. With three analyses, the chance of not having a Type I error is (0.95)(0.95)(0.95) = (0.95)3 = 0.857, or about 86%. This means that there is about a 14% chance of having at least one Type I error. And so on, as we see in Table 11-1. ANOVA is a more powerful approach because it lets us test differences among three or more groups in just one test.
The F Statistic as an Expansion of the z and t Statistics



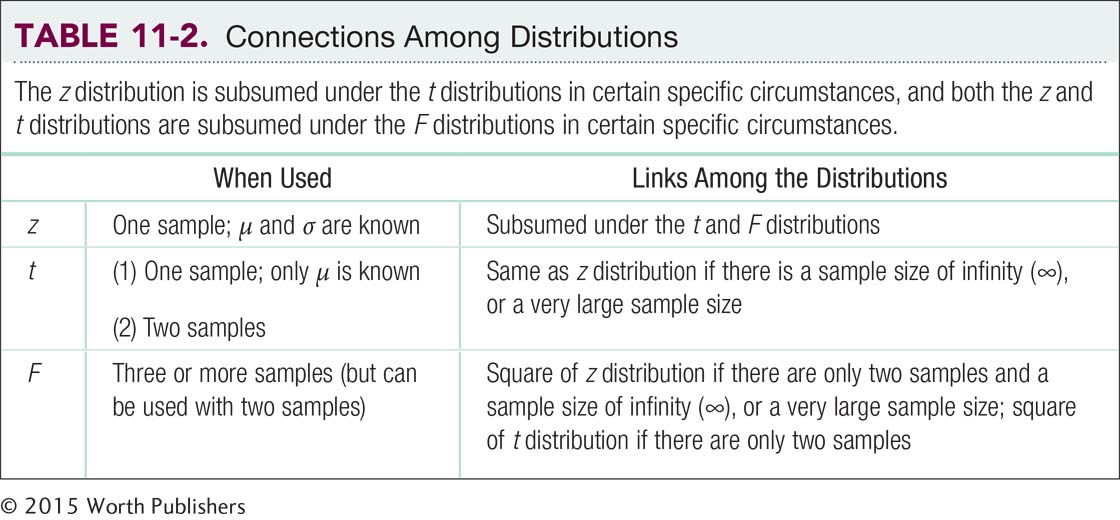
We use F distributions because they allow us to conduct a single hypothesis test with multiple groups. F distributions are more conservative versions of the z distribution and the t distributions. Just as the z distribution is still part of the t distributions, the t distributions are also part of the F distributions—
Analysis of variance (ANOVA) is a hypothesis test typically used with one or more nominal (and sometimes ordinal) independent variables (with at least three groups overall) and a scale dependent variable.
MASTERING THE CONCEPT
11-
The hypothesis tests that we have learned so far—
The F Distributions for Analyzing Variability to Compare Means
The F statistic is a ratio of two measures of variance: (1) between-
groups variance, which indicates differences among sample means, and (2) within- groups variance, which is essentially an average of the sample variances.
Comparing the height between men and women demonstrates that the F statistic is a ratio of two measures of variance: (1) between-
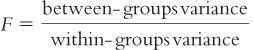
Between-
groups variance is an estimate of the population variance, based on the differences among the means.
Let’s begin with the numerator, called between-groups variance because it is an estimate of the population variance, based on the differences among the means. A big number in the numerator indicates a great deal of distance (or spread) between the means, suggesting that they come from different populations. A small number in the numerator indicates very little distance (or spread) between the means, suggesting that they come from the same population. With more than two means, we can’t use simple subtraction to find a number that indicates how spread apart they are, so we calculate the variance among the sample means. For example, if we wanted to compare how fast people talk in Vancouver, Memphis, Chicago, and Toronto, then the number representing between-
Within-
groups variance is an estimate of the population variance, based on the differences within each of the three (or more) sample distributions.
The denominator of the F statistic is called the within-groups variance, an estimate of the population variance, based on the differences within each of the three (or more) sample distributions. For example, not everyone living in Vancouver, Memphis, Chicago, or Toronto speaks at the same pace. There are within-
To calculate the F statistic, we simply divide the between-
To summarize, we can think of within-
The F Table
The F table is an expansion of the t table. Just as there are many t distributions represented in the t table—
The F table for two samples can even be used as a t test; the numbers are the same except that the F is based on variance and the t on the square root of the variance, the standard deviation. For example, if we look in the F table under two samples for a sample size of infinity for the equivalent of the 95th percentile, we see 2.71. If we take the square root of this, we get 1.646. We can find 1.645 on the z table for the 95th percentile and on the t table for the 95th percentile with a sample size of infinity. (The slight differences are due only to rounding decisions.) The connections between the z, t, and F distributions are summarized in Table 11-2.
The Language and Assumptions for ANOVA
Here is a simple guide to the language that statisticians use to describe different kinds of ANOVAs (Landrum, 2005). The word ANOVA is almost always preceded by two adjectives that indicate: (1) the number of independent variables; and (2) the research design (between-
A one-
way ANOVA is a hypothesis test that includes both one nominal independent variable with more than two levels and a scale dependent variable.
A between-
groups ANOVA is a hypothesis test in which there are more than two samples, and each sample is composed of different participants.
Study 1. What would you call an ANOVA with year in school as the only independent variable and Consideration of Future Consequences (CFC) scores as the dependent variable? Answer: A one-
A within-
groups ANOVA is a hypothesis test in which there are more than two samples, and each sample is composed of the same participants; also called a repeated-measures ANOVA.
Study 2. What if you wanted to test the same group of students every year? Answer: You would use a one-
Study 3. And what if you wanted to add gender to the first study, something we explore in the next chapter? Now you have two independent variables: year in school and gender. Answer: You would use a two-
All ANOVAs, regardless of type, share the same three assumptions that represent the optimal conditions for valid data analysis.
Assumption 1. Random selection is necessary if we want to generalize beyond a sample. Because of the difficulty of random sampling, researchers often substitute convenience sampling and then replicate their experiment with a new sample.
Assumption 2. A normally distributed population allows us to examine the distributions of the samples to get a sense of what the underlying population distribution might look like. This assumption becomes less important as the sample size increases.
Homoscedastic populations are those that have the same variance; homoscedasticity is also called homogeneity of variance.
Heteroscedastic populations are those that have different variances.
Assumption 3. Homoscedasticity (also called homogeneity of variance) assumes that the samples all come from populations with the same variances. (Heteroscedasticity means that the populations do not all have the same variance.) Homoscedastic populations are those that have the same variance. Heteroscedastic populations are those that have different variances.
What if your study doesn’t match these ideal conditions? You may have to throw away your data—
CHECK YOUR LEARNING
| Reviewing the Concepts |
|
|
| Clarifying the Concepts | 11- |
The F statistic is a ratio of what two kinds of variance? |
| 11- |
What are the two types of research designs for a one- |
|
| Calculating the Statistics | 11- |
Calculate the F statistic, writing the ratio accurately, for each of the following cases:
|
| Applying the Concepts | 11- |
Consider the research on multitasking that we explored in Chapter 9 (Mark, Gonzalez, & Harris, 2005). Let’s say we compared three conditions to see which one would lead to the quickest resumption of a task following an interruption. In one condition, the control group, no changes were made to the working environment. In the second condition, a communication ban was instituted from 1:00 to 3:00 P.M. In the third condition, a communication ban was instituted from 11:00 A.M. to 3:00 P.M. We recorded the time, in minutes, until work on an interrupted task was resumed.
|
Solutions to these Check Your Learning questions can be found in Appendix D.