8.1 Confidence Intervals
A point estimate is a summary statistic from a sample that is just one number used as an estimate of the population parameter.
MASTERING THE CONCEPT
8-
In studies on gender differences in mathematics performance, researchers calculate a mean difference by subtracting a mean score for girls from a mean score for boys. All three summary statistics—
Interval Estimates
An interval estimate is based on a sample statistic and provides a range of plausible values for the population parameter.
An interval estimate is based on a sample statistic and provides a range of plausible values for the population parameter. Interval estimates are frequently used by the media, often when reporting political polls, and are usually constructed by adding and subtracting a margin of error from a point estimate.
EXAMPLE 8.1
For example, a Marist poll asked 938 adult respondents in the United States to select from five choices the word or phrase that they found “most annoying in conversation” (http:/
Because 47 − 3.2 = 43.8 and 47 + 3.2 = 50.2, the interval estimate for “whatever” is 43.8% to 50.2% (Figure 8-2). Interval estimates provide a range of plausible values, not just one statistic.

Intervals and Overlap
When two intervals, like those for “whatever” and “you know,” do not overlap, we conclude that the population means are likely different. In the population, it seems that “whatever” really is more annoying than “you know.” However, when two intervals do overlap, like those for “it is what it is” and “anyway,” then it is plausible that the two phrases are perceived as equal—
Pay attention to whether the interval estimates overlap. “You know” came in second, with 25%, giving an interval estimate of 21.8% to 28.2%. There’s no overlap with the first-
A confidence interval is an interval estimate based on a sample statistic; it includes the population mean a certain percentage of the time if the same population is sampled from repeatedly.
Language Alert! The terms “margin of error,” “interval estimate,” and “confidence interval” all represent the same idea. Specifically, a confidence interval is an interval estimate based on a sample statistic; it includes the population mean a certain percentage of the time if the same population is sampled from repeatedly. (Note: We are not saying that we are confident that the population mean falls in the interval; we are merely saying that we expect to find the population mean within a certain interval a certain percentage of the time—
The confidence interval is centered around the mean of the sample. A 95% confidence level is most commonly used, indicating the 95% that falls between the two tails (i.e., 100% − 5% = 95%). Note the terms used here: The confidence level is 95%, but the confidence interval is the range between the two values that surround the sample mean.
Calculating Confidence Intervals with z Distributions
The symmetry of the z distribution makes it easy to calculate confidence intervals.
EXAMPLE 8.2
We already conducted hypothesis testing in Example 7.5 in Chapter 7 for a study on calories consumed by patrons of different Starbucks stores that either did or did not post the calories on their menus (Bollinger, Leslie, & Sorensen, 2010). Here is how confidence intervals can help us listen more closely to the story these data tell. The population mean was 247 calories, and we considered 201 to be the population standard deviation. The 1000 people in the sample consumed a mean of 232 calories. When we conducted hypothesis testing, we centered the curve around the mean according to the null hypothesis, the population mean of 247. We determined critical values based on this mean and compared the sample mean to these cutoffs. The test statistic (−2.36) was beyond the critical z statistic, so we rejected the null hypothesis. The data led us to conclude that people going to those Starbucks that posted calories consumed fewer calories, on average, than people going to those Starbucks that did not post calories.
There are several steps to calculating a confidence interval.
STEP 1: Draw a picture of a distribution that will include the confidence interval.
We draw a normal curve (Figure 8-3) that has the sample mean, 232, at its center, instead of the population mean, 247.
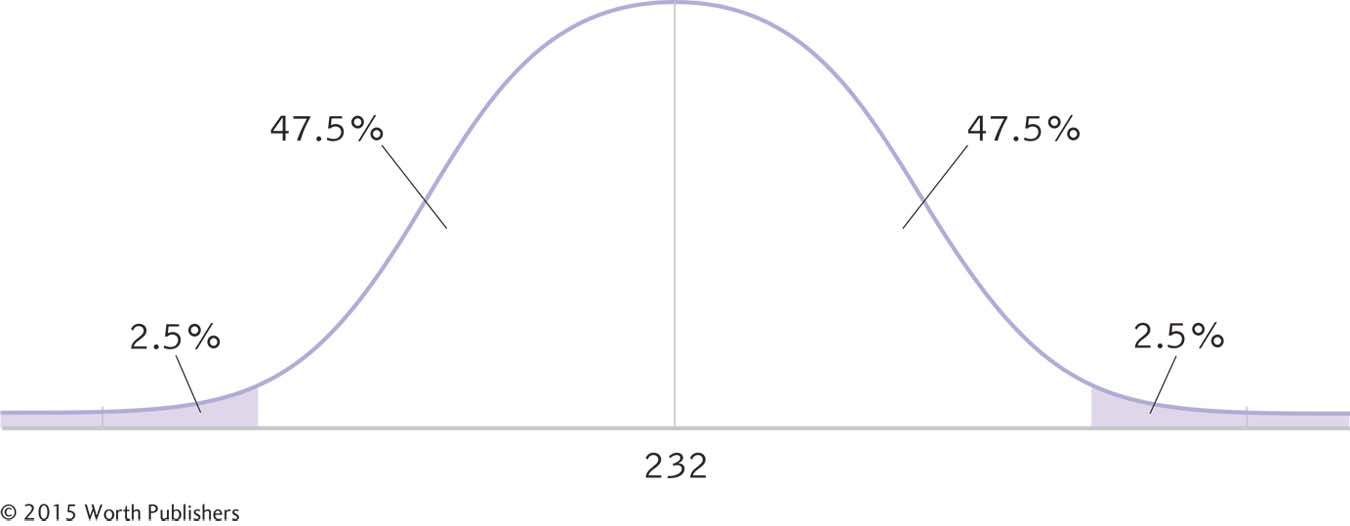
A 95% Confidence Interval, Part I
To begin calculating a confidence interval for a z distribution, we draw a normal curve, place the sample mean at its center, and indicate the percentages within and beyond the confidence interval.
STEP 2: Indicate the bounds of the confidence interval on the drawing.
We draw a vertical line from the mean to the top of the curve. For a 95% confidence interval, we also draw two small vertical lines to indicate the middle 95% of the normal curve (2.5% in each tail, for a total of 5%).
The curve is symmetric, so half of the 95% falls above and half falls below the mean. Half of 95 is 47.5, so we write 47.5% in the segments on either side of the mean. In the tails beyond the two lines that indicate the end of the middle 95%, we also write the appropriate percentages. You can see these percentages in Figure 8-3.
STEP 3: Determine the z statistics that fall at each line marking the middle 95%.
To do this, we turn back to the versatile z table in Appendix B. The percentage between the mean and each of the z scores is 47.5%. When we look up this percentage in the z table, we find a z statistic of 1.96. (Note that this is identical to the cutoffs for the z test; this will always be the case because the p level of 0.05 corresponds to a confidence level of 95%.) We can now add the z statistics of −1.96 and 1.96 to the curve, as seen in Figure 8-4.
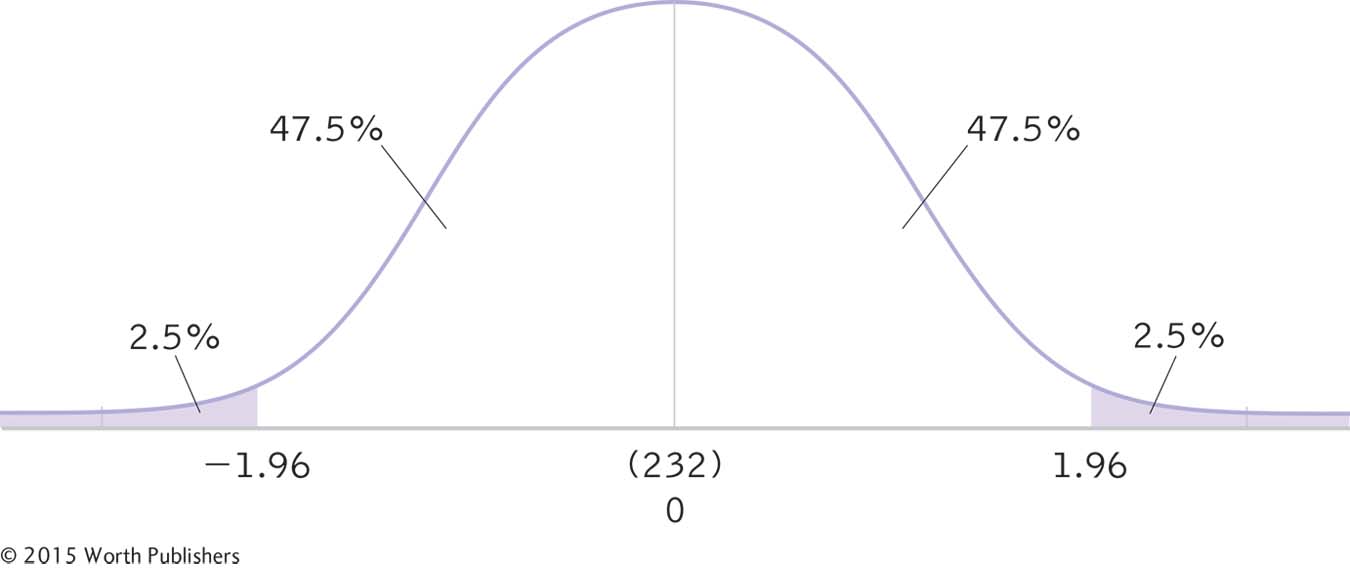
A 95% Confidence Interval, Part II
The next step in calculating a confidence interval is identifying the z statistics that indicate each end of the interval. Because the curve is symmetric, the z statistics will have the same magnitude—
STEP 4: Turn the z statistics back into raw means.
We use the formula for this conversion, but first we identify the appropriate mean and standard deviation. There are two important points to remember. First, we center the interval around the sample mean (not the population mean). So we use the sample mean of 232 in the calculations. Second, because we have a sample mean (rather than an individual score), we use a distribution of means. So we calculate standard error as the measure of spread:
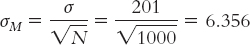
Notice that this is the same standard error that we calculated in Example 7.5 in Chapter 7 when we conducted a hypothesis test.
Using this mean and standard error, we calculate the raw mean at each end of the confidence interval, and add them to the curve, as in Figure 8-5:
Mlower = −z(σM) + Msample = −1.96(6.356) + 232 = 219.54
Mupper = z(σM) + Msample = 1.96(6.356) + 232 = 244.46
The 95% confidence interval, reported in brackets as is typical, is [219.54, 244.46].
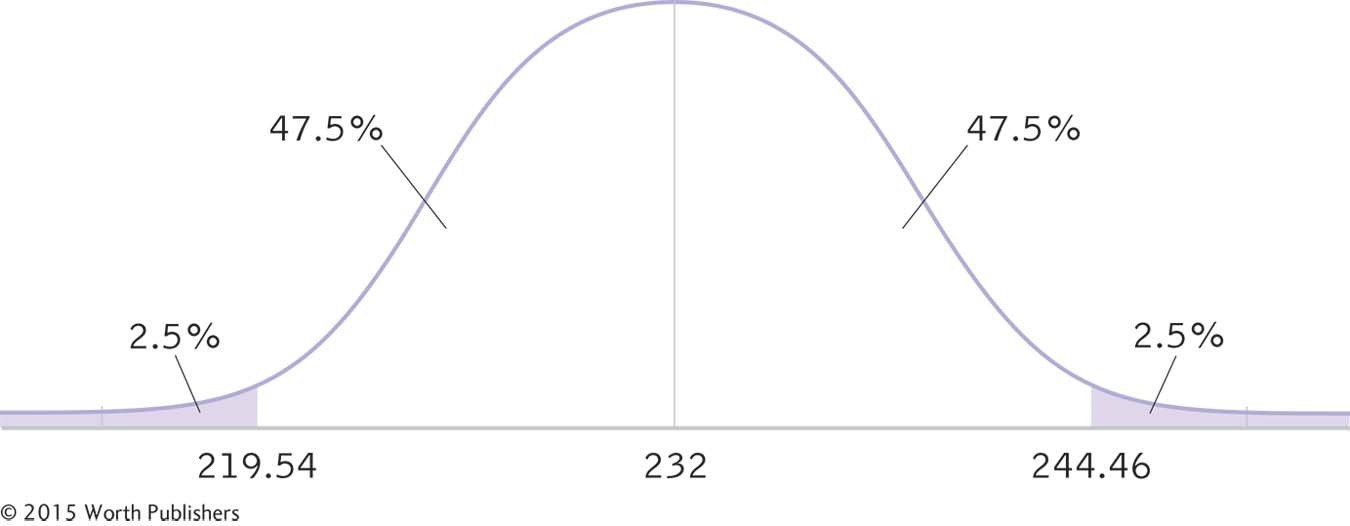
A 95% Confidence Interval, Part III
The final step in calculating a confidence interval is converting the z statistics that indicate each end of the interval into raw means.
MASTERING THE FORMULA
8-
STEP 5: Check that the confidence interval makes sense.
The sample mean should fall exactly in the middle of the two ends of the interval.
219.54 − 232 = −12.46 and 244.46 − 232 = 12.46
We have a match. The confidence interval ranges from 12.46 below the sample mean to 12.46 above the sample mean. We can think of this number, 12.46, as the margin of error.
To recap the steps for the creation of a confidence interval for a z statistic:
Draw a normal curve with the sample mean in the center.
Indicate the bounds of the confidence interval on either end, and write the percentages under each segment of the curve.
Look up the z statistics for the lower and upper ends of the confidence interval in the z table. These are always −1.96 and 1.96 for a 95% confidence interval around a z statistic.
Page 191Convert the z statistics to raw means for each end of the confidence interval.
Check your answer; each end of the confidence interval should be exactly the same distance from the sample mean.
If we were to sample 1000 customers at the Starbucks that post calories on their menus from the same population over and over, the 95% confidence interval would include the population mean 95% of the time. Note that the population mean for customers at the Starbucks that do not post calories, 247, falls outside of this interval. So, it is not plausible that the sample of customers at Starbucks that post calories comes from the population according to the null hypothesis—
CHECK YOUR LEARNING
| Reviewing the Concepts |
|
|
| Clarifying the Concepts | 8- |
Why are interval estimates better than point estimates? |
| Calculating the Statistics | 8- |
If 21% of voters want to raise taxes, with a margin of error of 4%, what is the interval estimate? What is the point estimate? |
| Applying the Concepts | 8- |
In How It Works 7.2, we conducted a z test based on the following information adapted from a study by Adams (2012) that used the Consideration of Future Consequences (CFC) scale as the dependent variable. The population mean CFC score was 3.20, with a standard deviation of 0.70. The sample was 45 students who joined a career discussion group, and the study examined whether this might have changed CFC scores. The mean for this group was 3.45.
|
Solutions to these Check Your Learning questions can be found in Appendix D.