nolanessentials3e

9.1 The t Distributions

The t distributions (note the plural) help us specify how confident we can be about research findings. We want to know whether we can generalize what we have learned about one sample to a larger population. The t test, based on the t distributions, tells us how confident we can be that the sample differs from the larger population.

The t distributions are more versatile than the z distribution because we can use them when (a) we don’t know the population standard deviation, and (b) we compare two samples. Figure 9-1 demonstrates that there are many t distributions—one for each possible sample size. Just as we are less likely to believe gossip from only one or two people, we are less certain about what the population distribution really looks like when we have a small sample size. The uncertainty of a small sample size means that the t distributions become flatter and more spread out. However, as the sample size gets larger, the t distributions begin to merge with the z distribution because we gain confidence as more participants are added to a study, just as we become increasingly confident in gossip that is repeated by many independent sources.

Figure 9.1: FIGURE 9-1
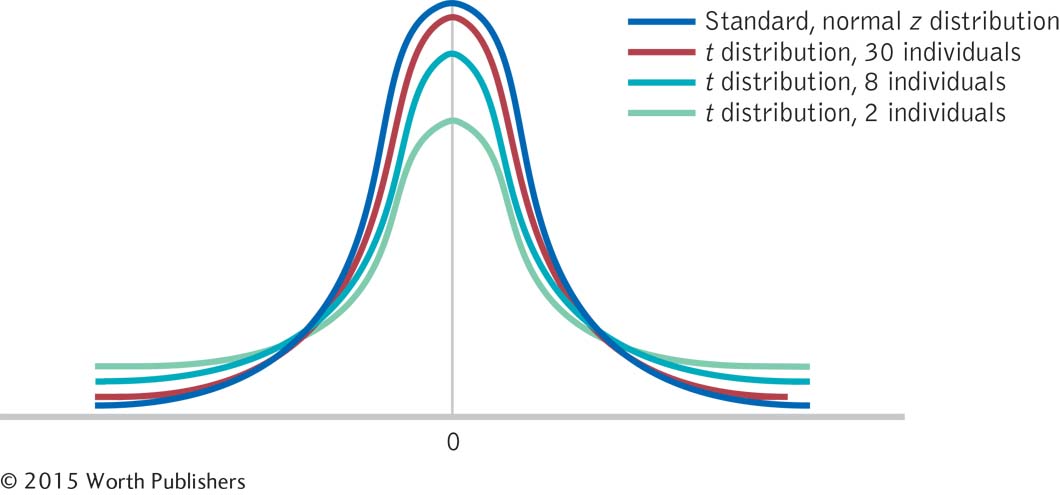
The Wider and Flatter t Distributions

Figure 9.1: For smaller samples (such as of 2 or 8 individuals), the t distributions are wider and flatter than the z distribution. However, as the sample size increases (such as of 30 individuals), the t distributions look more like the z distribution. This makes sense because a larger sample size would be more similar to the entire population than a smaller sample size.

215

Estimating Population Standard Deviation from a Sample

Before we conduct a single-sample t test, we must estimate the population standard deviation by using the sample standard deviation. Estimating the standard deviation is the only practical difference between conducting a z test with the z distribution and conducting a t test with a t distribution. Here is the sample standard deviation formula that we have used up until now:

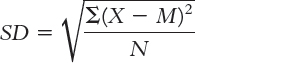
We need to make a correction to this formula to account for the fact that there is likely to be some level of error when we estimate the population standard deviation from a sample. Specifically, any given sample is likely to have somewhat less spread than does the entire population. One tiny alteration of this formula leads to a slightly larger and more accurate standard deviation. Instead of dividing by N, we divide by (N − 1) to get the mean of the squared deviations. Subtraction is the key. For example, if the numerator were 90 and the denominator (N) were 10, the answer would be 9; if we divide by (N − 1) = (10 − 1) = 9, the answer would be 10, a slightly larger value. So the formula is:

MASTERING THE FORMULA

9-1: The formula for standard deviation when estimating from a sample is:

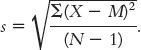
We subtract 1 from the sample size in the denominator to correct for the probability that the sample standard deviation slightly underestimates the actual standard deviation in the population.

Multitasking If multitasking reduces productivity in a sample, we can estimate the amount by which multitasking reduces productivity in a larger population.

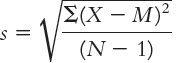
Notice that we call this standard deviation s instead of SD. We still use Latin rather than Greek letters because it is a statistic (from a sample) rather than a parameter (from a population). From now on, we will calculate the standard deviation in this way because we will be estimating the population standard deviation.

Let’s apply the new formula for standard deviation to a familiar activity: multitasking. Employees were observed at one of two high-tech companies for more than 1000 hours (Mark, Gonzalez, & Harris, 2005). The employees spent just 11 minutes, on average, on one project before being interrupted. Moreover, after each interruption, they needed an average of 25 minutes to get back to the original project! So maybe the reality is that multitasking actually reduces overall productivity.

216

Suppose you were a manager at one of these firms and decided to reserve a period from 1:00 to 3:00 each afternoon during which employees could not interrupt one another, but might still be interrupted by people outside the company. To test the intervention, you observe five employees and develop a score for each—time spent on a selected task before being interrupted. Here are the fictional data: 8, 12, 16, 12, and 14 minutes. In this case, we treat 11 minutes as the population mean, but we do not know the population standard deviation.

EXAMPLE 9.1

To calculate the estimated standard deviation for the population, there are two steps.

STEP 1: Calculate the sample mean.

Even though we know the population mean (11), we use the sample mean to calculate the corrected sample standard deviation. The mean for these scores is:

STEP 2: Use the sample mean in the corrected formula for the standard deviation.

Remember, the easiest way to calculate the numerator under the square root sign is by first organizing the data into columns, as shown here:

X	X − M	(X − M)²
8	−4.4	19.36
12	−0.4	0.16
16	3.6	12.96
12	−0.4	0.16
14	1.6	2.56

The numerator is:

𝚺(X − M)² = 𝚺(19.36 + 0.16 + 12.96 + 0.16 + 2.56) = 35.2

217

A Simple Correction: N − 1 When estimating variability, subtracting one person from a sample of four makes a big difference. Subtracting one person from a sample of thousands makes only a small difference.

And given a sample size of 5, the corrected standard deviation is:

Calculating Standard Error for the t Statistic

MASTERING THE FORMULA

9-2: The formula for standard error when we estimate from a sample is:

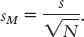
It only differs from the formula for standard error we learned previously in that we use s instead of σ because we’re working from a sample instead of a population.

We now have an estimate of the standard deviation of the distribution of scores, but not an estimate of the spread of a distribution of means, the standard error. As we did with the z distribution, we make the spread smaller to reflect the fact that a distribution of means is less variable than a distribution of scores. We do this in exactly the same way that we adjusted for the z distribution. We divide s by 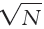. The formula for the standard error as estimated from a sample, therefore, is:

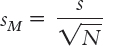
Notice that we have replaced σ with s because we are using the corrected sample standard deviation rather than the population standard deviation.

EXAMPLE 9.2

Here’s how we convert the corrected standard deviation of 2.97 to a standard error. The sample size was 5, so we divide by the square root of 5:

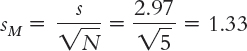
So the standard error is 1.33. Just as the central limit theorem predicts, the standard error for the distribution of sample means is smaller than the standard deviation of sample scores. (Note: This step can lead to a common mistake. Because we implemented a correction when calculating s, students often want to implement an extra correction here by dividing by . Do not do this! We still divide by 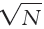in this step. There is no need for a further correction to the standard error.)

218

Using Standard Error to Calculate the t Statistic

The t statistic indicates the distance of a sample mean from a population mean in terms of the estimated standard error.

We now have the tools necessary to conduct the single-sample t test. When conducting a single-sample t test, we calculate the t statistic, the distance of a sample mean from a population mean in terms of the estimated standard error. We introduce the formula for that t statistic here, and in the next section we go through all six steps for a single-sample t test. The formula is identical to that for the z statistic, except that it uses estimated standard error. Here is the formula for the t statistic for a distribution of means:

MASTERING THE FORMULA

9-3: The formula for the single-sample t statistic is:

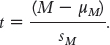
It only differs from the formula for the z statistic in that we use s_M (estimated from a sample) instead of σ_M (based on the population).

Note that the denominator is the only difference between this formula for the t statistic and the formula used to compute the z statistic for a sample mean. The corrected denominator makes the t statistic smaller and thereby reduces the probability of having an extreme t statistic. That is, a t statistic is not as extreme as a z statistic; in scientific terms, it’s more conservative.

EXAMPLE 9.3

The t statistic for the sample of five scores representing minutes until interruptions is:

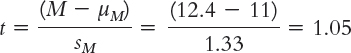
As part of the six steps of hypothesis testing, the t statistic can help us make an inference about whether the ban on internal interruptions affected the average number of minutes until an interruption.

CHECK YOUR LEARNING

Reviewing the Concepts		We use t distributions when we do not know the population standard deviation and are comparing only two groups. The two groups may be a sample and a population, or two samples as part of a within-groups design or a between-groups design. The formula for the t statistic for a single-sample t test is the same as the formula for the z statistic for a distribution of means, except that we use estimated standard error in the denominator rather than the actual standard error for the population. We calculate estimated standard error by dividing by N − 1, rather than dividing by N, when calculating standard error.
Clarifying the Concepts	9-1	What is the t statistic?
Calculating the Statistics	9-2	Calculate the standard deviation for a sample (SD) and as an estimate of the population (s) using the following data: 6, 3, 7, 6, 4, 5.
	9-3	Calculate standard error for t for the data given in Check Your Learning 9-2.
Applying the Statistics	9-4	In the discussion of a study on multitasking (Mark et al., 2005), we imagined a follow-up study in which we measured time until a task was interrupted. For each of the five employees, let’s now examine time until work on the initial task was resumed at 20, 19, 27, 24, and 18 minutes. Remember that the original research showed it took 25 minutes on average for an employee to return to a task after being interrupted. What distribution would be used in this situation? Explain your answer. Determine the appropriate mean and standard deviation (or standard error) for this distribution. Show all your work; use symbolic notation and formulas where appropriate. Calculate the t statistic.

Solutions to these Check Your appropriate. Learning questions can be found in Appendix D.

219