11.1 Conducting an Independent-Samples t Test
An independent-
The independent-
263
A Distribution of Differences Between Means
Because we have different people in each condition of the study, we cannot create a difference score for each person. We’re looking at overall differences between two independent groups, so we need to develop a new type of distribution, a distribution of differences between means.
MASTERING THE CONCEPT
11.1: An independent-
Let’s use the Chapter 6 data about heights to demonstrate how to create a distribution of differences between means. Let’s say that we were planning to collect data on two groups of three people each and wanted to determine the comparison distribution for this research scenario. Remember that in Chapter 6, we used the example of a population of 140 college students from the authors’ classes. We described writing the height of each student on a card and putting the 140 cards in a bowl.
EXAMPLE 11.1
Let’s use that example to create a distribution of differences between means. We’ll walk through the steps for this process.
STEP 1: We randomly select three cards, replacing each after selecting it, and calculate the mean of the heights listed on them. This is the first group.
STEP 2: We randomly select three other cards, replacing each after selecting it, and calculate their mean. This is the second group.
STEP 3: We subtract the second mean from the first.
That’s really all there is to it—
Here’s an example using the three steps.
STEP 1: We randomly select three cards, replacing each after selecting it, and find that the heights are 61, 65, and 72. We calculate a mean of 66 inches. This is the first group.
STEP 2: We randomly select three other cards, replacing each after selecting it, and find that the heights are 62, 65, and 65. We calculate a mean of 64 inches. This is the second group.
STEP 3: We subtract the second mean from the first: 66 − 64 = 2. (Note that it’s fine to subtract the first from the second, as long as we’re consistent in the arithmetic.)
264
We repeat the three-
Figure 11-
The Six Steps of the Independent-Samples t Test
EXAMPLE 11.2
Does the price of a product influence how much you like it? If you’re told that your sister’s new flat-

© Lenscap/Alamy
Economics researchers from Northern California, not far from prime wine country, wondered whether enjoyment of wine is influenced by price (Plassmann, O’Doherty, Shiv, & Rangel, 2008). In part of their study, they randomly assigned some wine drinkers to taste wine that was said to cost $10 per bottle and others to taste the same wine at a supposed price of $90 per bottle. (Note that we’re altering some aspects of the design and statistical analysis of this study for teaching purposes, but the results are similar.) The researchers asked participants to rate how much they liked the wine; they also used functional magnetic resonance imaging (fMRI), a brain-
265
We will conduct an independent-
- Mean “liking ratings” of the wine
- “$10” wine: 1.5 2.3 2.8 3.4
- “$90” wine: 2.9 3.5 3.5 4.9 5.2
STEP 1: Identify the populations, distribution, and assumptions.
In terms of determining the populations, this step is similar to that for the paired-
| Hypothesis Test | Number of Samples | Comparison Distribution |
|---|---|---|
| z test | One | Distribution of means |
| Single- |
One | Distribution of means |
| Paired- |
Two (same participants) | Distribution of mean difference scores |
| Independent- |
Two (different participants) | Distribution of differences between means |
As usual, the comparison distribution is based on the null hypothesis. As with the paired-
Summary: Population 1: People told they are drinking wine from a $10 bottle. Population 2: People told they are drinking wine from a $90 bottle.
The comparison distribution will be a distribution of differences between means based on the null hypothesis. The hypothesis test will be an independent-
266
STEP 2: State the null and research hypotheses.
This step for an independent-
Summary: Null hypothesis: On average, people drinking wine they were told was from a $10 bottle give it the same rating as people drinking wine they were told was from a $90 bottle—
STEP 3: Determine the characteristics of the comparison distribution.
This step for an independent-
Because we have two samples for an independent-
- Calculate the corrected variance for each sample. (Notice that we’re working with variance, not standard deviation.)
- Pool the variances. Pooling involves taking an average of the two sample variances while accounting for any differences in the sizes of the two samples. Pooled variance is an estimate of the common population variance.
- Convert the pooled variance from squared standard deviation (that is, variance) to squared standard error (another version of variance) by dividing the pooled variance by the sample size, first for one sample and then again for the second sample. These are the estimated variances for each sample’s distribution of means.
- Add the two variances (squared standard errors), one for each distribution of sample means, to calculate the estimated variance of the distribution of differences between means.
- Calculate the square root of this form of variance (squared standard error) to get the estimated standard error of the distribution of differences between means.
Notice that stages (a) and (b) are an expanded version of the usual first calculation for a t test. Instead of calculating one corrected estimate of standard deviation, we’re calculating two for an independent-
267
(a) We calculate corrected variance for each sample (corrected variance is the one we learned in Chapter 9 that uses N − 1 in the denominator). First, we calculate variance for X, the sample of people told they are drinking wine from a $10 bottle. Be sure to use the mean of the ratings of the $10 wine drinkers only, which we calculate to be 2.5. Notice that the symbol for this variance uses s2, instead of SD2 (just as the standard deviation used s instead of SD in the previous t tests). Also, we included the subscript X to indicate that this is variance for the first sample, whose scores are arbitrarily called X. (Remember, don’t take the square root. We want variance, not standard deviation.)
| X | X − M | (X − M)2 |
|---|---|---|
| 1.5 | −1.0 | 1.00 |
| 2.3 | −0.2 | 0.04 |
| 2.8 | 0.3 | 0.09 |
| 3.4 | 0.9 | 0.81 |
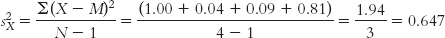
Now we do the same for Y, the people told they are drinking wine from a $90 bottle. Remember to use the mean for Y; it’s easy to forget and use the mean we calculated earlier for X. We calculate the mean for Y to be 4.0. The subscript Y indicates that this is the variance for the second sample, whose scores are arbitrarily called Y. (We could call these scores by any letter, but statisticians tend to call the scores in the first two samples X and Y.)
| Y | Y − M | (Y − M)2 |
|---|---|---|
| 2.9 | −1.1 | 1.21 |
| 3.5 | −0.5 | 0.25 |
| 3.5 | −0.5 | 0.25 |
| 4.9 | 0.9 | 0.81 |
| 5.2 | 1.2 | 1.44 |
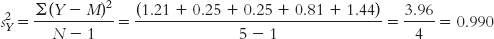
Pooled variance is a weighted average of the two estimates of variance—
(b) We pool the two estimates of variance. Because there are often different numbers of people in each sample, we cannot simply take their mean. We mentioned earlier in this book that estimates of spread taken from smaller samples tend to be less accurate. So we weight the estimate from the smaller sample a bit less and weight the estimate from the larger sample a bit more. We do this by calculating the proportion of degrees of freedom represented by each sample. Each sample has degrees of freedom of N − 1. We also calculate a total degrees of freedom that sums the degrees of freedom for the two samples. Here are the calculations:
268
MASTERING THE FORMULA
11-
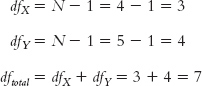
Using these degrees of freedom, we calculate a sort of average variance. Pooled variance is a weighted average of the two estimates of variance—
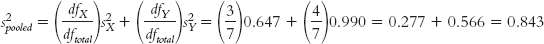
MASTERING THE FORMULA
11-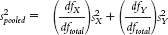 . This formula takes into account the size of each sample. A larger sample has a larger degrees of freedom in the numerator, and that variance therefore has more weight in the pooled variance calculations.
. This formula takes into account the size of each sample. A larger sample has a larger degrees of freedom in the numerator, and that variance therefore has more weight in the pooled variance calculations.
(Note: If we had exactly the same number of participants in each sample, this would be an unweighted average—
(c) Now that we have pooled the variances, we have an estimate of spread. This is similar to the estimate of the standard deviation in the previous t tests, but now it’s based on two samples (and is an estimate of variance rather than standard deviation). The next calculation in the previous t tests was dividing standard deviation by  to get standard error. In this case, we divide by N instead of
to get standard error. In this case, we divide by N instead of  . Why? Because we are dealing with variances, not standard deviations. Variance is the square of standard deviation, so we divide by the square of
. Why? Because we are dealing with variances, not standard deviations. Variance is the square of standard deviation, so we divide by the square of  , which is simply N. We do this once for each sample, using pooled variance as the estimate of spread. We use pooled variance because an estimate based on two samples is better than an estimate based on one. The key here is to divide by the appropriate N: in this case, 4 for the first sample and 5 for the second sample.
, which is simply N. We do this once for each sample, using pooled variance as the estimate of spread. We use pooled variance because an estimate based on two samples is better than an estimate based on one. The key here is to divide by the appropriate N: in this case, 4 for the first sample and 5 for the second sample.
MASTERING THE FORMULA
 11-
11- For the second sample, the formula is:
For the second sample, the formula is: 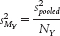 . Note that because we’re dealing with variance, the square of standard deviation, we divide by N, the square of
. Note that because we’re dealing with variance, the square of standard deviation, we divide by N, the square of  — the denominator for standard error.
— the denominator for standard error.
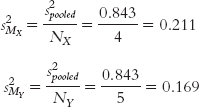
(d) In stage (c), we calculated the variance versions of standard error for each sample, but we want only one such measure of spread when we calculate the test statistic. So, we combine the two variances, similar to the way in which we combined the two estimates of variance in stage (b). This stage is even simpler, however. We merely add the two variances together. When we sum them, we get the variance of the distribution of differences between means, symbolized as 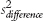 . Here are the formula and the calculations for this example:
. Here are the formula and the calculations for this example:
269
MASTERING THE FORMULA
11-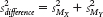 .
.
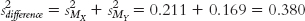
(e) We now have paralleled the two calculations of the previous t tests by doing two things: (1) We calculated an estimate of spread (we made two calculations, one for each sample, then combined them), and (2) we then adjusted the estimate for the sample size (again, we made two calculations, one for each sample, then combined them). The main difference is that we have kept all calculations as variances rather than standard deviations. At this final stage, we convert from variance form to standard deviation form. Because standard deviation is the square root of variance, we do this by simply taking the square root:
MASTERING THE FORMULA
11-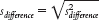 .
.
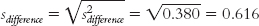
Summary: The mean of the distribution of differences between means is: μX − μY = 0. The standard deviation of the distribution of differences between means is: sdifference = 0.616.
STEP 4: Determine critical values, or cutoffs.
This step for the independent-
Summary: The critical values, based on a two-
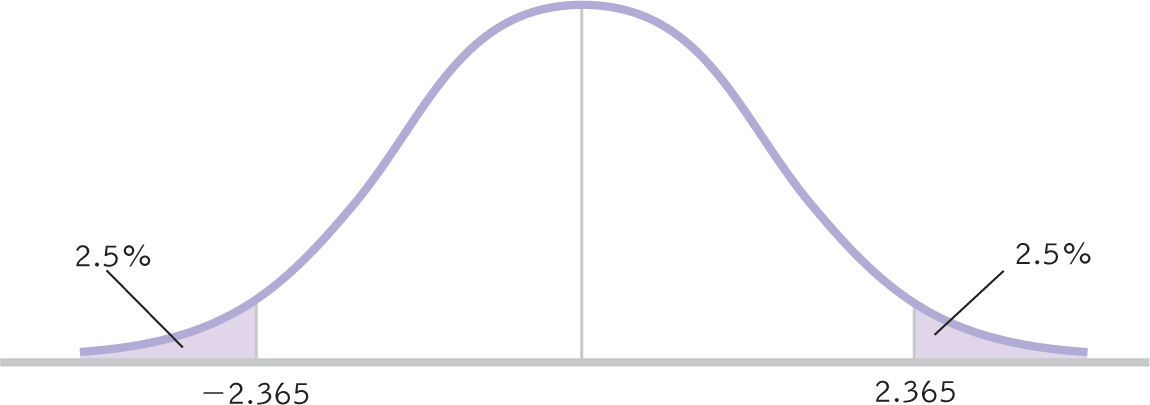
Figure 11-
STEP 5: Calculate the test statistic.
This step for the independent-
MASTERING THE FORMULA
 11-
11-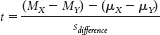 . We subtract the difference between means according to the null hypothesis, usually 0, from the difference between means in the sample. We then divide this by the standard deviation of the differences between means. Because the difference between means according to the null hypothesis is usually 0, the formula for the test statistic is often abbreviated as:
. We subtract the difference between means according to the null hypothesis, usually 0, from the difference between means in the sample. We then divide this by the standard deviation of the differences between means. Because the difference between means according to the null hypothesis is usually 0, the formula for the test statistic is often abbreviated as:  .
.
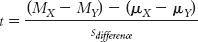
As in previous t tests, the test statistic is calculated by subtracting a number based on the populations from a number based on the samples, then dividing by a version of standard error. Because the population difference between means (according to the null hypothesis) is almost always 0, many statisticians choose to eliminate the latter part of the formula. So the formula for the test statistic for an independent-
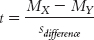
You might find it easier to use the first formula, however, as it reminds us that we are subtracting the population difference between means according to the null hypothesis (0) from the actual difference between the sample means. This format more closely parallels the formulas of the test statistics we calculated in Chapter 9.
270
Summary: 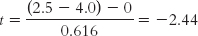
STEP 6: Make a decision.
This step for the independent-
Summary: Reject the null hypothesis. It appears that those told they are drinking wine from a $10 bottle give it lower ratings, on average, than those told they are drinking from a $90 bottle (as shown by the curve in Figure 11-3).

Figure 11-
This finding documents the fact that people report liking a more expensive wine better than a less expensive one—
Reporting the Statistics
To report the statistics as they would appear in a journal article, follow standard APA format, including the degrees of freedom, the value of the test statistic, and the p value associated with the test statistic. (Note that because the t table in Appendix B only includes the p values of 0.10, 0.05, and 0.01, we cannot use it to determine the actual p value for the test statistic. Unless we use software, we can only report whether or not the p value is less than the critical p level.) In the current example, the statistics would read:
t(7) = −2.44, p < 0.05
In addition to the results of hypothesis testing, we would also include the means and standard deviations for the two samples. We calculated the means in step 3 of hypothesis testing, and we also calculated the variances (0.647 for those told they were drinking from a $10 bottle and 0.990 for those told they were drinking from a $90 bottle). We can calculate the standard deviations by taking the square roots of the variances. The descriptive statistics can be reported in parentheses as:
($10 bottle: M = 2.5, SD = 0.80; $90 bottle: M = 4.0, SD = 0.99)
271
CHECK YOUR LEARNING
Reviewing the Concepts
- When we conduct an independent-
samples t test, we cannot calculate individual difference scores. That is why we compare the mean of one sample with the mean of the other sample. - The comparison distribution is a distribution of differences between means.
- We use the same six steps of hypothesis testing that we used with the z test and with the single-
sample and paired- samples t tests. - Conceptually, the t test for independent samples makes the same comparisons as the other t tests. However, the calculations are different, and critical values are based on degrees of freedom from two samples.
Clarifying the Concepts
- 11-
1 In what situation do we conduct a paired-samples t test? In what situation do we conduct an independent- samples t test? - 11-
2 What is pooled variance?
Calculating the Statistics
- 11-
3 Imagine you have the following data from two independent groups: - Group 1: 3, 2, 4, 6, 1, 2
- Group 2: 5, 4, 6, 2, 6
- Compute each of the following calculations needed to complete your final calculation of the independent-
samples t test. - Calculate the corrected variance for each group.
- Calculate the degrees of freedom and pooled variance.
- Calculate the variance version of standard error for each group.
- Calculate the variance of the distribution of differences between means, then convert this number to standard deviation.
- Calculate the test statistic.
Applying the Concepts
- 11-
4 In Check Your Learning 11-3, you calculated several statistics; now let’s consider a context for those numbers. Steele and Pinto (2006) examined whether people’s level of trust in their direct supervisor was related to their level of agreement with a policy supported by that leader. They found that the extent to which subordinates agreed with their supervisor was statistically significantly related to trust and showed no relation to gender, age, time on the job, or length of time working with the supervisor. We have presented fictional data to re- create these findings, where group 1 represents employees with low trust in their supervisor and group 2 represents the high- trust employees. The scores presented are the level of agreement with a decision made by a leader, from 1 (strongly disagree) to 7 (strongly agree). - Group 1 (low trust in leader): 3, 2, 4, 6, 1, 2
- Group 2 (high trust in leader): 5, 4, 6, 2, 6
- State the null and research hypotheses.
- Identify the critical values and make a decision.
- Write your conclusion in a formal sentence that includes presentation of the statistic in APA format.
- Explain why your results are different from those in the original research, despite having a similar mean difference.
Solutions to these Check Your Learning questions can be found in Appendix D.
272