Concept 43.2: Interactions within and among Species Affect Population Dynamics and Species Distributions

Individual members of a population usually vary in their survival and reproduction, a point we will return to in Concept 43.4. Even so, we can sum up the contributions of all members to obtain the total population growth rate. The resulting value is exactly equivalent to what we obtained by using averages in Concept 42.2. There we showed that the population growth rate equals the average individual’s contribution (the per capita growth rate, r) multiplied by the number of individuals in the population (N). If r does not change, population size either grows at an ever-faster rate (if r is positive) or gradually shrinks to zero (if r is negative).

The value of r is not fixed, however, because of intraspecific (Latin, “within species”) competition: mutually detrimental interactions among members of the same species that occur because they use the same limiting resources. As population density increases, per capita resource availability shrinks, the per capita growth rate decreases, and overall population growth slows (see Concept 42.4). This negative feedback (see Concept 1.2) dramatically alters the growth trajectory: instead of growing toward infinity, the population stops growing and fluctuates around a carrying capacity (K).

Interspecific interactions can modify per capita growth rates

Per capita growth rates are affected by interspecific as well as intraspecific interactions, and we can study how these interactions affect population dynamics by including both of them in an equation for population growth. The word equation on p. 874 describes the growth of a single population in which intraspecific competition causes r to decrease as population density increases. A competing species will decrease r by an additional amount that depends on its density:

Notice that to describe this interaction, we need to write a pair of equations: one for species A and one for species B. Each equation consists of an expression that describes the growth of one species in the absence of the other, minus an expression that describes the effect of the other species.

Interspecific interactions other than competition can be described in a similar way. Depending on the type of interaction, we must either subtract or add the effect of the other species (see Figure 43.1A). In consumer–resource interactions, we subtract the effect of the consumer species (e.g., the predator) in the equation for the resource species (e.g., the prey), since the consumer increases the mortality of the resource species. Conversely, we add an effect of the resource species in the equation for the consumer, since the consumer benefits from the presence of the resource. In mutualistic interactions, we add an effect of each mutualist to the equation for the other. In commensal interactions, we add a term in the equation of the species that benefits, and in amensal interactions, we subtract a term in the equation of the species that is harmed. (In these two types of interactions, equations for the partner species contain no reciprocal terms, because, by definition, the partner is unaffected by the interaction.)

APPLY THE CONCEPT: Interactions within and among species affect population dynamics and species distributions

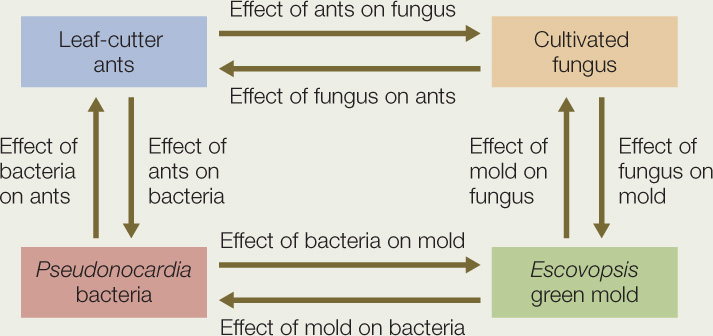
A leaf-cutter ant nest can be considered a community—an ecological system (see Concepts 1.2 and 41.1) in which the species are components that interact with one another. Major components of the system are shown as labeled boxes, and their interactions as arrows between those boxes.

Use the description of interactions within leaf-cutter ant nests in the opening story of this chapter to answer the following questions:

1. What is the sign of the following direct effects of each species on another?
   
2. Explain for each interaction the mechanism by which the fitness of interacting individuals is affected.
3. To which of the five categories of interspecific interactions does each pairwise interaction belong?
4. Explain how the spatial distribution of the green mold Escovopsis might affect the spatial distribution of leaf-cutter ant colonies.

Interspecific interactions affect population dynamics and can lead to extinction

Because interspecific interactions modify per capita growth rates, populations show different dynamics in the presence and absence of other species. The Russian ecologist Georgii F. Gause explored the effects of interspecific interactions on populations of several species of the protist Paramecium (see Figure 20.6). He grew these unicellular organisms in single-species cultures and in cultures containing either a competing species of Paramecium or a protist predator, Didinium. To understand the results, Gause used both word equations, such as the one we gave earlier, and mathematical expressions of the same interactions. In the decades since Gause’s work, mathematical models have proved to be important for understanding how interspecific interactions affect population dynamics. In the case of competition, all models lead to the following conclusions:

• The presence of a competitor always reduces population growth rate. In FIGURE 43.3A, notice that the slope of the curve of population density versus time is shallower in the presence of a competitor, because the competitor reduces the per capita growth rate from what it would be with intraspecific density dependence alone.
  

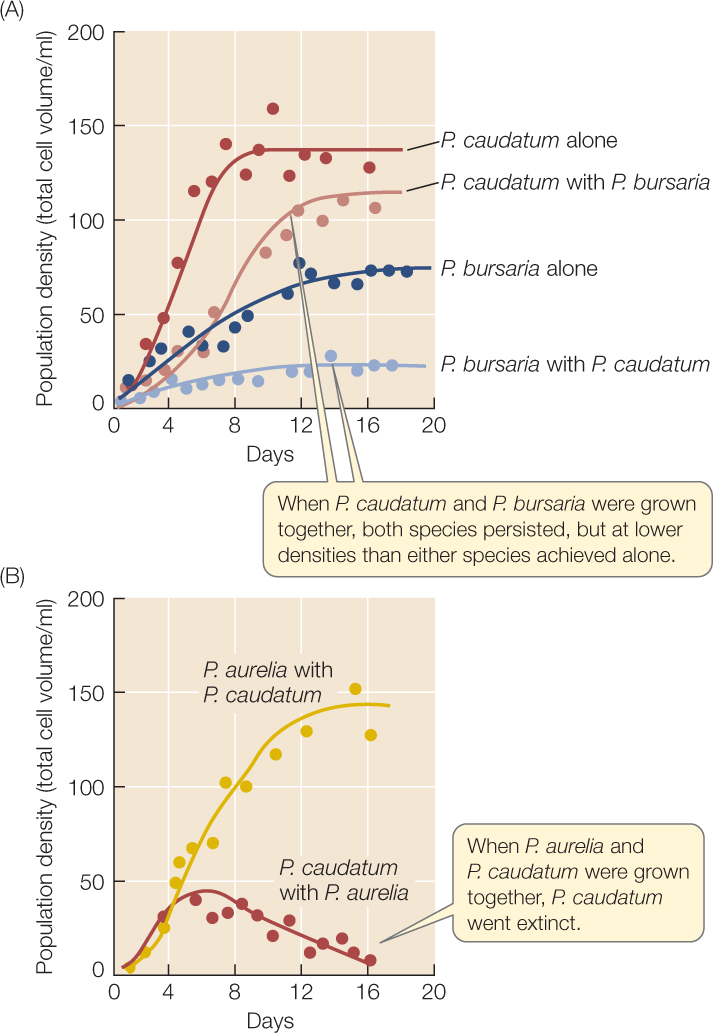  Figure 43.3: Interspecific Competition Affects Population Growth (A) Some species of the unicellular protist Paramecium are able to coexist, but their populations grow more slowly, and reach lower equilibrium densities, when a competitor is present. (B) Competition between some Paramecium species results in local extinction of one species.
• When two competitors coexist, as in Figure 43.3A, they achieve lower equilibrium population densities than either would achieve alone.
• In some cases, as in FIGURE 43.3B, one competitor drives the other extinct.

Other types of interspecific interactions also affect population growth rates and average densities:

• In all interspecific interactions, the per capita growth rate of at least one species is modified by the presence of the other, sometimes positively and sometimes negatively.
• In all interspecific interactions, the average population density of at least one species differs in the presence and in the absence of the other species. Population densities are increased in species for which the interaction is positive and are decreased in species for which the interaction is negative.
• In interactions that have negative effects—that is, consumer− resource interactions, competition, and amensalism—local extinction of one or both of the interacting species is possible.

Interspecific interactions can affect species distributions

We have seen that a species may be absent from a particular location because barriers to dispersal have prevented the species from colonizing it (see Concept 41.4), or because the environment is unfavorable for the species’ population growth (see Concept 42.3). We can now see that other species—not just physical conditions—may determine whether a population can persist. A site may be unfavorable because it lacks suitable prey or because it harbors a competitor or predator; conversely, an otherwise unfavorable site may become favorable if a mutualist is present.

FIGURE 43.4 shows an example of how competitive interactions can restrict the habitats in which species occur. The rock barnacle (Semibalanus balanoides) and Poll’s stellate barnacle (Chthamalus stellatus) compete for space on rocky shorelines of the North Atlantic Ocean. Adult barnacles attach themselves permanently to rocks and filter food particles from the water that flows past them; therefore, occupying a space amounts to having the opportunity to feed. The planktonic (swimming) larvae of both S. balanoides and C. stellatus settle in the intertidal zone and metamorphose into immobile adults. There is little overlap between the areas occupied by adults; the smaller stellate barnacles generally live higher in the intertidal zone, where they face longer periods of exposure to air and desiccation than do rock barnacles.

Figure 43.4: Interspecific Competition Can Restrict Distributions The left-hand bar for each species shows the zone over which larvae settle, and thus the potential adult distribution. The right-hand bar shows the actual adult distribution. Competition with rock barnacles restricts stellate barnacles to a smaller portion of the intertidal zone than they could otherwise occupy.

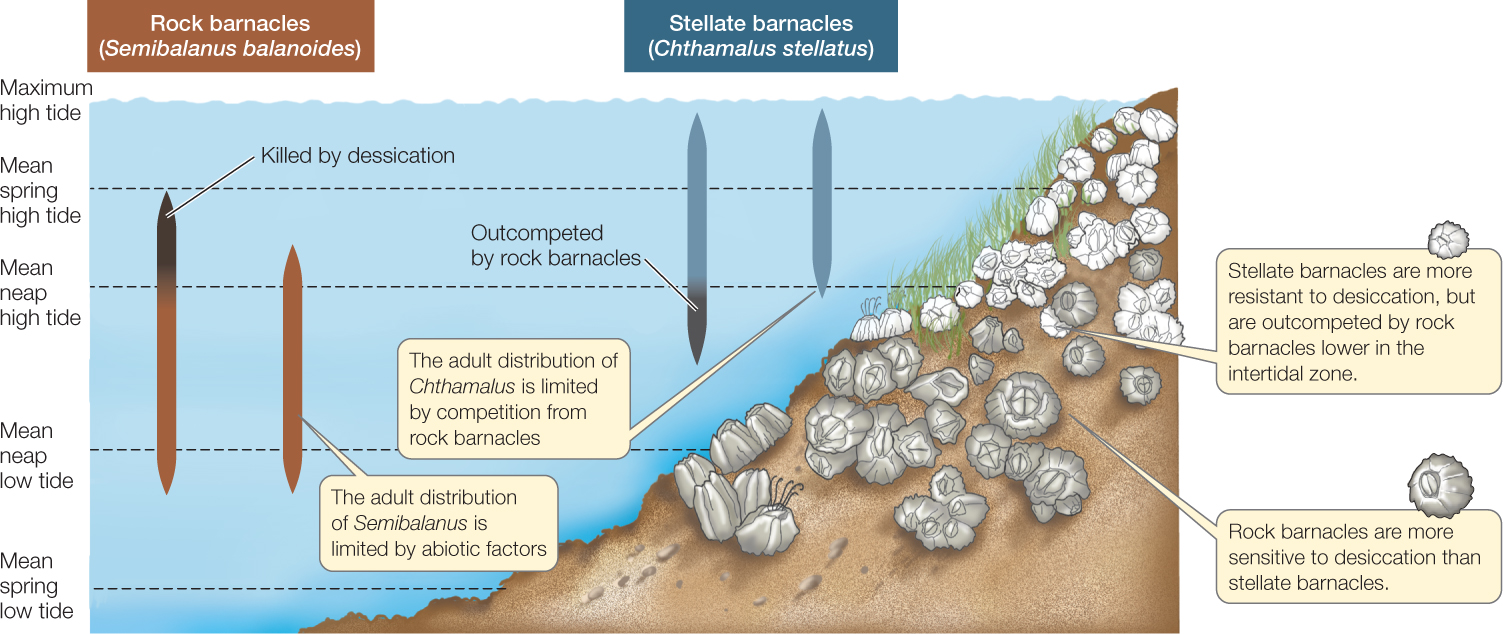
In a famous experiment conducted more than 50 years ago, Joseph Connell removed each of the species from its characteristic zone and observed the response of the other species. Stellate barnacle larvae settled in large numbers throughout much of the intertidal zone, including the lower levels where rock barnacles are normally found, but they thrived at those levels only when rock barnacles were absent. The rock barnacles grew so fast when present that they smothered, crushed, or undercut the stellate barnacles. By outcompeting them for space, rock barnacles made the lower intertidal zone unsuitable for stellate barnacles. In contrast, removing stellate barnacles from higher in the intertidal zone did not lead to their replacement by rock barnacles; the rock barnacles were less tolerant of desiccation and so failed to thrive there even when stellate barnacles were absent.

Rarity advantage promotes species coexistence

Mathematical models of interspecific interactions have been useful not only in helping us understand how these interactions affect population dynamics and species distributions, but also by giving us insights into the conditions that allow interacting species to coexist.

Models of interspecific competition indicate that two competitors will coexist when individuals of each species suppress their own per capita growth rate more than they suppress the per capita growth rate of their competitor. In other words, intraspecific competition must be stronger than interspecific competition: you harm yourself more than you harm your competitor. When this is the case, a species gains a growth advantage when it is rare—that is, when it is at a low density and its competitor is at a high density—and this rarity advantage prevents the population from decreasing to zero. The result is coexistence.

One mechanism that can cause intraspecific competition to be stronger than interspecific competition is resource partitioning: differences between competing species in resource use. Individuals of the same species, which use very similar resources, will suppress their own per capita resource availability more than they suppress that of the competitor, unless the competitor uses identical resources. But this is unlikely, and if differences in resource use are sufficiently large, competing species can coexist (FIGURE 43.5).

Figure 43.5: Resource Partitioning Can Cause Intraspecific Competition to Be Greater Than Interspecific Competition When two species differ in their use of resources, individuals will have a greater effect on the availability of resources to individuals of their own species than to individuals of the other species. In this hypothetical scenario, birds of species A eat smaller seeds on average than birds of species B. Individuals of species A affect the food supply for their own species (smaller seeds) more than they affect the food supply for species B (larger seeds), and vice versa. In other words, the two species partition, or divide up, the seed resource.

Paramecium aurelia, for instance, outcompetes both P. caudatum and P. bursaria, but the latter two species can coexist (see Figure 43.3A) because P. bursaria can feed on bacteria in the low-oxygen sediment layer at the bottom of culture flasks, a habitat that P. caudatum cannot tolerate. This partitioning of habitat is possible because P. bursaria harbors symbiotic algae that provide it with additional oxygen as a by-product of algal photosynthesis.

In the case of predators and prey, a number of processes can result in a rarity advantage that protects prey from being driven extinct by their predators. For example, prey may become harder to find as they become rarer because they can all hide in the best refuges; or they may be able to invest more in their defenses when they are at low densities and have more resources available per capita. Predators may also stop looking for rare prey and switch to a more abundant prey type.

Alternatively, some other limiting factor (such as availability of nest sites) may prevent the predators from becoming numerous enough to eat all the prey. The effect of such processes is that per capita growth rates may rebound when prey become rare, thus making their extinction less likely.

The examples of two-species interspecific interactions that we have discussed do not occur in isolation. As may already be apparent, they form parts of a larger web of interactions that connects any given species to many others living in the same area.