Finding the True Direction of an Airplane

An airplane has an air speed of \(400\) km/h and is headed east. Find the true direction of the airplane relative to the ground if there is a northwesterly wind of \(80~\text{km}/~\text{h}\).

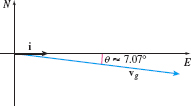
Solution This is the same situation from Example 8 of Section 10.3. There, we found the velocity of the airplane relative to the ground is \( \mathbf{v}_{\mathrm{g}}=( 400+40\sqrt{2}) \mathbf{i}-40\sqrt{2 }\mathbf{j}\).

The angle \(\theta\) between \(\mathbf{v}_{\mathrm{g}}\) and the vector \( \mathbf{i}\) (the positive \(x\)-axis) is given by \[ \begin{eqnarray*} \cos \theta &=&\dfrac{\mathbf{v}_{\mathrm{g}}\,{\cdot}\, \mathbf{i}}{\Vert \mathbf{v}_{\mathrm{g}}\Vert \Vert \mathbf{i}\Vert }&=&\dfrac{ 400+40\sqrt{2}}{460.06}\approx 0.9924 \\[5pt] \theta &\approx &\cos ^{-1}(0.9924) \approx 7.07^\circ \end{eqnarray*} \]

The true direction of the plane is approximately \(7.07^\circ\) south of east. See Figure 37.