Graphing a Function of Two Variables

Graph each function:

  1. \(z=f(x,y)=1-x-y\)
  2. \(z=f(x,y)=x^{2}+4y^{2}\)
  3. \(z=f(x,y)=\sqrt{x^{2}+y^{2}}\)

Planes in space are discussed in Section 10.6, pp. 737-740.

Solution (a) The graph of the equation \(z=1-x-y\), or \(x+y+z=1\), is a plane. The intercepts are the points \((1,0,0),\) \((0,1,0)\), and \((0,0,1)\). See Figure 6.

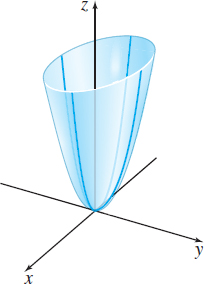
(b) The graph of the equation \(z=x^{2}+4y^{2}\) is an elliptic paraboloid whose vertex is at the origin. See Figure 7.

Quadric surfaces are discussed in Section 10.7, pp. 744-751.

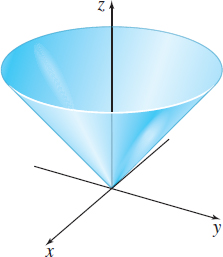
(c) The equation \(z=f(x,y) =\sqrt{x^{2}+y^{2}}\) is equivalent to \(z^{2}=x^{2}+y^{2}\), where \(z\geq 0\). The graph of the equation is part of a circular cone whose vertex is at the origin. Since \( z\geq 0,\) the graph of \(f\) is the upper nappe of the cone. See Figure 8.

Figure 6 \(z=f (x,y) =1-x-y\)
Figure 7 \(z=f(x, y)=x^{2} + 4y^{2}\)
Figure 8 \(z=f (x,y) = \sqrt{x^2 +y^2}\)