10.6 Equations of Lines and Planes in SpacePrinted Page 733
OBJECTIVES
When you finish this section, you should be able to:
- Find a vector equation of a line in space (p. 733)
- Find parametric equations of a line in space (p. 734)
- Find symmetric equations of a line in space (p. 734)
- Determine whether two distinct lines are skew, parallel, or intersecting (p. 736)
- Find an equation of a plane (p. 737)
- Determine whether two distinct planes are parallel or intersecting (p. 738)
- Find the distance from a point to a plane (p. 739)
1 Find a Vector Equation of a Line in SpacePrinted Page 733
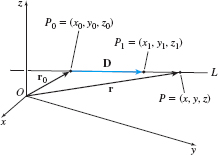
In space, a line is determined when we know a point on the line and its direction If P0=(x0,y0,z0) and P1=(x1,y1,z1) are two distinct points on a line, then the vector D represented by the directed line segment →P0P1 is a nonzero vector that gives the direction of the line. Note that D is not unique. Any two points on the line can be used to find the direction of the line. See Figure 51.
If r0 denotes the vector →OP0 and r denotes the vector →OP of any point P=(x,y,z) on the line, then the vector r−r0 is parallel to the vector D. That is, r−r0=tDfor some scalar tr=r0+tD
THEOREM Vector Equation of a line
A vector equation of a line in the direction D≠0 and containing the point P0=(x0,y0,z0) is \bbox[5px, border:1px solid black, #F9F7ED]{ \mathbf{r}=\mathbf{r}_{0}+t\mathbf{D} }
where \mathbf{r}_{0} is the vector \overrightarrow{{\it OP}_{0}} , \mathbf{r} is the vector \overrightarrow{\it OP}, and P= ( x,y,z) is any point on the line.
734
In the vector equation \mathbf{r}=\mathbf{r}_{0}+t\mathbf{D} of a line, both the vector \mathbf{r}_{0} and the vector \mathbf{D} are known. To locate other points P on the line, we assign values to the scalar t. For each real number t, we obtain a vector whose terminal point is on the line. Vector equations of a line are not unique since the choice of a point on the line and the choice of the vector representing the direction of the line can vary.
EXAMPLE 1Finding a Vector Equation of a Line in Space
Find a vector equation of the line containing the points P_{0}\,\,{=}\,\,(1,2,-1) and P_{1}=(4,3,-2).
Solution The vector \mathbf{D} in the direction from P_{0}=(1,2,-1) to P_{1}=(4,3,-2) is \begin{equation*} \mathbf{D}=\overrightarrow{P_{0}P_{1}}=3\mathbf{i+j-k} \end{equation*}
If we let \mathbf{r}_{0}=\mathbf{i}+2\mathbf{j-k}, then a vector equation of the line is \mathbf{r}=\mathbf{r}_{0}+t \mathbf{D}=\mathbf{i}+2\mathbf{j}-\mathbf{k} +t (3\mathbf{i}+\mathbf{j}-\mathbf{k})=(1+3t)\mathbf{i}+(2+t)\mathbf{j} +(-1-t)\mathbf{k}
NOW WORK
NEED TO REVIEW?
Parametric equations are discussed in Section 9.1, pp. 637-642.
2 Find Parametric Equations of a Line in SpacePrinted Page 734
The vector equation of a line in the direction \mathbf{D}=a\mathbf{i}+b \mathbf{j}+c\mathbf{k} and containing the point P_{0}=(x_{0},y_{0},z_{0}) can be written as \mathbf{r}=\mathbf{r}_{0}+t\mathbf{D}, where \mathbf{ r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k} and \ \mathbf{r}_{0}=x_{0}\mathbf{i} +y_{0}\mathbf{j}+z_{0}\mathbf{k}. Then \begin{eqnarray*} x\mathbf{i}+y\mathbf{j}+z\mathbf{k}&=&(x_{0}\mathbf{i}+y_{0}\mathbf{j}+z_{0} \mathbf{k})+t\,(a\mathbf{i}+b\mathbf{j}+c\mathbf{k})\\[3pt] &=& ( x_{0}+at) \mathbf{i}+\left( y_{0}+bt\right)\!\mathbf{j}+\left( z_{0}+ct\right)\! \mathbf{k } \end{eqnarray*}
Since two vectors are equal if and only if their corresponding components are equal, we have \bbox[5px, border:1px solid black, #F9F7ED]{\bbox { x=x_{0}+at\qquad y=y_{0}+bt\qquad z=z_{0}+ct }}
These equations are parametric equations of the line, and the variable t is the parameter. Points (x,y,z) on the line are obtained by assigning values to the parameter t. For example, when t=0, we obtain the point (x_{0},y_{0},z_{0}) on the line.
EXAMPLE 2Finding Parametric Equations of a Line in Space
Find parametric equations of the line containing the point (2,-3,1) and in the direction of the vector 4\mathbf{i}+\dfrac{3}{4}\mathbf{j}-\mathbf{k}.
Solution Let (x_{0},y_{0},z_{0})=(2,-3,1) and a\mathbf{i}+b \mathbf{j}+c\mathbf{k}=4\mathbf{i}+\dfrac{3}{4}\mathbf{j}-\mathbf{k}. Then, the parametric equations of the line are x=x_{0}+at=2+4t\qquad y=y_{0}+bt=-3+\frac{3}{4}t\qquad z=z_{0}+ct=1-t
NOW WORK
3 Find Symmetric Equations of a Line in SpacePrinted Page 734
In the parametric equations x=x_{0}+at, \ y=y_{0}+bt, and z=z_{0}+ct , if the numbers a, b, and c (the components of the vector \mathbf{D}) are all nonzero, we can solve for t, obtaining \begin{equation*} t=\frac{x-x_{0}}{a}\qquad t=\frac{y-y_{0}}{b} \qquad t=\frac{z-z_{0}}{c} \end{equation*}
735
from which \bbox[5px, border:1px solid black, #F9F7ED]{\bbox { \dfrac{x-x_{0}}{a}=\dfrac{y-y_{0}}{b}=\dfrac{z-z_{0}}{c} }}
NOTE
The symmetric equations actually represent a pair of equations
\dfrac{x-x_0}{a}=\dfrac{y-y_{0}}{b}
and
\dfrac{x-x_{0}}{a} = \dfrac{z-z_0}{c}.
These equations are referred to as symmetric equations of a line.
EXAMPLE 3Finding Symmetric Equations of a Line in Space
Find symmetric equations of the line containing the point (1,-1,2) and in the direction of the vector 5\mathbf{i}-2\mathbf{j}+3\mathbf{k}.
Solution The components of the vector 5\mathbf{i}-2\mathbf{j}+3 \mathbf{k} are all nonzero. So, we use a=5, b=-2, and c=3 and the coordinates of the point (1,-1,2) to obtain the symmetric equations \frac{x-1}{5}=\frac{y+1}{-2}=\frac{z-2}{3}
Parametric and symmetric equations of a line are not unique. For example, since the vector -10\,\mathbf{i}+4\mathbf{j}-6\mathbf{k} is parallel to 5\mathbf{i}-2\mathbf{j}+3\mathbf{k}, the symmetric equations of the line described in Example 3 can be written as \begin{equation*} \frac{x-1}{-10}=\frac{y+1}{4}=\frac{z-2}{-6} \end{equation*}
NOW WORK
If one of the components of \mathbf{D} equals 0, the symmetric equations have a different form. For example, if \mathbf{D}=a\mathbf{i}+b\mathbf{j}+c \mathbf{k} and a=0, but b\neq 0 and c\neq 0, the symmetric equations of the line are written as x=x_{0}\qquad \frac{y-y_{0}}{b}=\frac{z-z_{0}}{c}
where P_{0}=\left( x_{0},y_{0},z_{0}\right) is a point on the line. This particular line lies in the plane x=x_{0}.
EXAMPLE 4Finding Symmetric Equations of a Line
Find symmetric equations of the line that contains the point (5,-2, 3) and is in the direction of the vector \mathbf{D=} 3\mathbf{i}-2\mathbf{k}.
Solution For \mathbf{D=} 3\mathbf{i}-2\mathbf{k}, a=3, b=0, and c=-2. So, symmetric equations in the direction \mathbf{D} are \dfrac{x-5}{3}=\frac{z-3}{-2}\qquad y=-2
NOW WORK
EXAMPLE 5Analyzing Symmetric Equations of a Line
A line is defined by the symmetric equations \dfrac{x-6}{3}=\dfrac{y+2}{1}=\dfrac{z+3}{-2}.
- (a) Find a vector in the direction of the line.
- (b) Find two points on the line.
Solution (a) From the denominators of the symmetric equations, we find a=3, b=1, and c=-2. So, {\bf D}= 3\mathbf{i}+\mathbf{j} -2\mathbf{k} is a vector in the direction of the line.
(b) Since the line is defined by the symmetric equations \dfrac{x-6}{3}=\dfrac{y+2}{1}=\dfrac{z+3}{-2}, one point on the line is ( 6,-2,-3) . To find a second point, we assign a value to x say, x=0. Then \begin{eqnarray*} \frac{0-6}{3} &=&\frac{y+2}{1}=\frac{z+3}{-2} \\[4pt] -2 &=&\frac{y+2}{1}=\frac{z+3}{-2} \end{eqnarray*}
736
Now we solve for y and z, and find y=-4 and z=1. So, another point on the line is (0,-4,1).
NOW WORK
4 Determine Whether Two Distinct Lines Are Skew, Parallel, or IntersectingPrinted Page 736
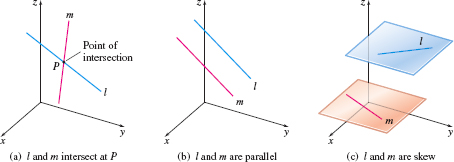
In the plane, two distinct lines either intersect or are parallel. In space, two distinct lines intersect, are parallel, or are skew. The lines intersect when they have exactly one point in common. The lines are parallel when they lie in the same plane but do not intersect. The lines are skew if they do not intersect and are not parallel. Figure 52 illustrates these possibilities.
As an example of skew lines, think of two airplanes, one flying at an altitude of 1000 m traveling north and the other flying at an altitude of 3000 m traveling east. Since they are flying at different altitudes, they will never collide (intersect). Since they are flying in different directions, they are not parallel.
EXAMPLE 6Determining Whether Two Lines Are Skew, Parallel, or Intersecting
Determine whether the lines given below intersect, are parallel, or are skew.
- (a) \begin{array}{l@{\quad}l@{\quad}l} & l_{1}\hbox{:}~ & ~\mathbf{r}_{1}=(3\mathbf{i}+3\mathbf{j}+ \mathbf{k})+t_{1}(\mathbf{i}-2\mathbf{j}+\mathbf{k}) \\ & l_{2}\hbox{:}~ & ~\mathbf{r}_{2}=(5\mathbf{i}+\mathbf{j}+\mathbf{k})+t_{2}( \mathbf{i}-4\mathbf{j}+3\mathbf{k})\\[3pt] \end{array}
- (b) \begin{array}{l@{\quad}l@{\quad}l} & l_{1}\hbox{:}~ & ~\mathbf{r}_{1}=(3\mathbf{i}+2\mathbf{ j}+\mathbf{k})+t_{1}\,(\mathbf{i}-\mathbf{j}+\mathbf{k}) \\ & l_{2}\hbox{:}~ & ~\mathbf{r}_{2}=(5\mathbf{i}+6\mathbf{j}+\mathbf{k} )+t_{2}(\mathbf{i}-\mathbf{j}+2\mathbf{k}) \end{array}
Solution (a) The line l_{1} is in the direction of the vector \mathbf{i}-2\mathbf{j}+\mathbf{k} and the line l_{2} is in the direction of the vector \mathbf{i}-4\mathbf{j}+3\mathbf{k}. Since these vectors are not parallel (do you know why?), l_{1} and l_{2} either intersect or are skew.
Suppose the lines intersect. Then there is some value of the parameter t_{1} and some value of the parameter t_{2} for which \mathbf{r}_{1}= \mathbf{r}_{2}. Since ~\mathbf{r}_{1}=(3+t_{1})\mathbf{i}+(3-2t_{1}) \mathbf{j}+(1+t_{1})\mathbf{k} and \mathbf{r}_{2}=(5+t_{2})\mathbf{i} +(1-4t_{2})\mathbf{j}+(1+3t_{2})\mathbf{k}, for \mathbf{r}_{1} to equal \mathbf{r}_{2}, we have \begin{equation*} (3+t_{1})\mathbf{i}+(3-2t_{1})\mathbf{j}+(1+t_{1})\mathbf{k}=(5+t_{2}) \mathbf{i}+(1-4t_{2})\mathbf{j}+(1+3t_{2})\mathbf{k}\qquad {\color{#0066A7}{\hbox{\(\mathbf{r}_{1}=\mathbf{r}_{2}\)}}} \end{equation*}
We equate the components of each vector to obtain 3+t_{1}=5+t_{2} \qquad 3-2t_{1}=1-4t_{2} \qquad 1+t_{1}=1+3t_{2}
737
The result is a system of three equations containing two variables. From the third equation, t_{1}=3t_{2}. Now substitute t_{1}=3t_{2} into each of the first two equations. \begin{equation*} \begin{array}{cllll} \begin{array}{rcl} 3+t_{1}&=&5+t_{2}\\ 3+3t_{2}&=&5+t_{2}\\ t_{2}&=&1 \end{array} & \ \ \ \ & \begin{array}{rcl} 3-2t_{1}&=&1-4t_{2}\\ 3-6t_{2}&=&1-4t_{2}\\ t_{2}&=&1 \end{array} & \ \ \ \ & {\color{#0066A7}{\hbox{\(t_{1}=3t_{2}\)}}} \end{array} \end{equation*}
Backsubstituting, we conclude t_{1}=3 and t_{2}=1. The point of intersection is found by substituting t_{1}=3 in l_{1} or t_{2}=1 in l_{2} . The result is \mathbf{r}_{1}=\mathbf{r}_{2}=6\mathbf{i}-3\mathbf{j}+4 \mathbf{k}. The point of intersection is (6,-3,4).
(b) The line l_{1} is in the direction of the vector \mathbf{i}- \mathbf{j}+\mathbf{k}, and the line l_{2} is in the direction of the vector \mathbf{i}-\mathbf{j}+2\mathbf{k}. These vectors are not parallel, so the lines l_{1} and l_{2} either intersect or are skew. As before, suppose they intersect. Then \mathbf{r}_{1}=\mathbf{r}_{2}\mathbf{\ }so that \begin{eqnarray*} &&( 3+t_{1}) \mathbf{i}+\left( 2-t_{1}\right)\! \mathbf{j}+( 1+t_{1}) \mathbf{k}=( 5+t_{2})\mathbf{i}+( 6-t_{2})\mathbf{j}+( 1+2t_{2}) \mathbf{k}\\[4pt] &&3+t_{1}=5+t_{2} \qquad 2-t_{1}=6-t_{2} \qquad 1+t_{1}=1+2t_{2} \qquad {\color{#0066A7}{\hbox{Equate components.}}} \end{eqnarray*}
Now substitute t_{1}=2t_{2} (from the third equation) into each of the first two equations. \begin{equation*} \begin{array}{cllll} \begin{array}{rcl} 3+t_{1}&=&5+t_{2} \\[6pt] 3+2t_{2}&=&5+t_{2} \\[6pt] t_{2}&=&2 \end{array} & \ \ \ \ & \begin{array}{rcl} 2-t_{1}&=&6-t_{2} \\[6pt] 2-2t_{2}&=&6-t_{2} \\[6pt] t_{2}&=&-4 \end{array} & \ \ \ \ & {\color{#0066A7}{\hbox{\(t_{1}=2t_{2}\)}}} \end{array} \end{equation*}
The system of equations has no solution, so the assumption that \mathbf{r} _{1}=\mathbf{r}_{2}\mathbf{,} for some t_{1} and some t_{2} is false. The lines are neither parallel nor intersecting, so they are skew.
CAUTION
When working with pairs of lines, be sure to use a different parameter for each line.
NOW WORK
5 Find an Equation of a PlanePrinted Page 737
The vector equation of a line is determined once a point on the line and a vector in the direction of the line are known. To determine the vector equation of a plane, we use a point on the plane and a vector perpendicular to the plane, a normal to the plane.
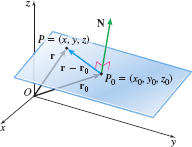
Suppose the point P_{0}=( x_{0},y_{0},z_{0}) is on a plane and suppose the nonzero vector \mathbf{N} is a normal to the plane. See Figure 53. Let P=( x,y,z) be any other point on the plane. Denote the vectors \overrightarrow{{\it OP}_{0}} and \overrightarrow{\it OP} by \mathbf{r }_{0} and \mathbf{r}, respectively. Since P is a point on the plane, the vector \mathbf{r}-\mathbf{r}_{0} is in the plane and is orthogonal to the vector \mathbf{N}. Then (\mathbf{r}-\mathbf{r}_{0})\,{\cdot}\, \mathbf{N} =0 .
THEOREM Vector Equation of a Plane
The vector equation of the plane containing the point P_{0} is (\mathbf{r}-\mathbf{r}_{0})\,{\cdot}\, \mathbf{N}=0
where \mathbf{r}_{0} is the vector \overrightarrow{{\it OP}_{0}}, \mathbf{r } is the vector \overrightarrow{\it OP} of any other point P on the plane, and \mathbf{N} is normal to the plane.
If the coordinates of P_{0} are ( x_{0},y_{0},z_{0}) and the vector \mathbf{N}=A\mathbf{i}+B\mathbf{j}+C\mathbf{k}, then \begin{eqnarray*} \left[ (x-x_{0})\mathbf{i}+(y-y_{0})\mathbf{j}+(z-z_{0})\mathbf{k} \right] \,{\cdot}\, (A\mathbf{i}+B\mathbf{j}+C\mathbf{k})& =&0 \\[5pt] A(x-x_{0})+B(y-y_{0})+C(z-z_{0})& =&0 \end{eqnarray*}
If D=Ax_{0}+By_{0}+Cz_{0}, we can write the equation as \begin{equation*} Ax+By+Cz=D \end{equation*}
Notice that the coefficients of x, y, and z in the equation are the components of the normal vector \mathbf{N}.
738
THEOREM General Equation of a Plane
An equation of the form \bbox[5px, border:1px solid black, #F9F7ED]{\bbox { Ax+By+Cz=D }}
with at least one of the numbers A, B, C not 0, is called the general equation of a plane, and the vector A\mathbf{i}+B\mathbf{j}+C \mathbf{k} is normal to this plane.
EXAMPLE 7Finding the General Equation of a Plane
Find the general equation of the plane containing the point ( 1,2,-1) if the vector \mathbf{N=\,}2\mathbf{i}+3\mathbf{j}-4 \mathbf{k} is normal to the plane. Then use the intercepts to graph the plane.
Solution The general equation of a plane is Ax+By+Cz=D, where A, B, and C are the components of a normal vector to the plane. Since the normal is \mathbf{N=\,}2\mathbf{i}+3\mathbf{j}-4\mathbf{k}, we have 2x+3y-4z=D
To find D, we use the point (1,2,-1). Then D=2(1) +3(2) -4(-1) =12. The general equation of the plane is 2x+3y-4z=12
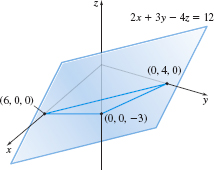
We find the intercepts by letting two variables equal zero and then solving for the third variable. For example, to find the x-intercept, we let y=0 and z=0. Then 2x=12 or x=6. Similarly, the y-intercept is 4 and the z-intercept is -3. Figure 54 illustrates how the intercepts are used to graph the plane.
NOW WORK
EXAMPLE 8Finding the General Equation of a Plane
Find the general equation of the plane containing the points P_{1}=(1,-1,2)\quad P_{2}=( 3,0,0)\quad P_{3}=(4,2,1)
Solution The vectors \mathbf{v}=\overrightarrow{P_{1}~P_{2}}=2 \mathbf{i}+\mathbf{j}-2\mathbf{k} and \mathbf{w}=\overrightarrow{P_{1}~P_{3} }=3\mathbf{i}+3\mathbf{j}-\mathbf{k} lie in the plane. The vector \begin{equation*} \mathbf{N}=\mathbf{v}\times \mathbf{w}=\left\vert \begin{array}{r@{\quad}r@{\quad}r} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] 2 & 1 & -2 \\[3pt] 3 & 3 & -1 \end{array} \right\vert =\left\vert \begin{array}{r@{\quad}r} 1 & -2 \\[3pt] 3 & -1 \end{array} \right\vert \mathbf{i}-\left\vert \begin{array}{r@{\quad}r} 2 & -2 \\[3pt] 3 & -1 \end{array} \right\vert \mathbf{j}+\left\vert \begin{array}{r@{\quad}r} 2 & 1 \\[3pt] 3 & 3 \end{array} \right\vert \mathbf{k}=5\mathbf{i}-4\mathbf{j}+3\mathbf{k} \end{equation*}
is orthogonal to both \mathbf{v} and \mathbf{w} and so is normal to the plane. Using the point (1,-1,2) and the vector \mathbf{N}, the general equation of the plane is \begin{eqnarray*} 5(x-1)-4(y+1)+3(z-2)& =&0 \\[2pt] 5x-5-4y-4+3z-6& =&0 \\[2pt] 5x-4y+3z& =&15 \end{eqnarray*}
NOW WORK
NOTE
The planes p_{1}: 2x+y-z=3 and p_{2}: 4x+2y-2z=6 are identical. Do you see why?
6 Determine Whether Two Distinct Planes Are Parallel or IntersectingPrinted Page 738
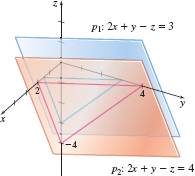
Two distinct planes are parallel if they have parallel normal vectors, that is, if \mathbf{N}_{1}=k\mathbf{N}_{2} for some scalar k\neq 0. For example, the distinct planes p_{1}:\quad 2x+y-z=3\qquad \hbox{and} \qquad p_{2}: 2x+y-z=4
739
are parallel because \mathbf{N}_{1}=2\mathbf{i}+\mathbf{j}-\mathbf{k}= \mathbf{N}_{2} and D_{1}=3 is not equal to D_{2}=4. See Figure 55.
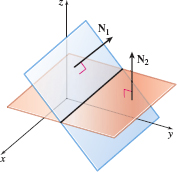
If the normal vectors of two planes are not parallel, then the planes intersect in a line, as shown in Figure 56. The line of intersection lies in both planes and so is perpendicular to both \mathbf{N} _{1} and \mathbf{N}_{2}.
EXAMPLE 9Determining the Line of Intersection of Two Nonparallel Planes
Find an equation of the line of intersection of the two planes x-2y+z=-1\quad \hbox{and}\quad 3x+y-z=4
Solution First notice that the normals \mathbf{N}_{1} = \mathbf{i}\, -\, 2\mathbf{j}\, +\, \mathbf{k} and \mathbf{N}_{2} = 3\mathbf{i}\, +\, \mathbf{j}\, -\, \mathbf{k} of the two planes are not parallel. To find an equation of the line of intersection, we need a point on the line and the direction of the line. Since the line of intersection is perpendicular to both \mathbf{N}_{1} and \mathbf{N}_{2}, it is parallel to the vector \mathbf{D}= \mathbf{N} _{1}\times \mathbf{N}_{2}. \mathbf{D=N}_{1}\times \mathbf{N}_{2}= \left|\begin{array}{r@{\quad}r@{\quad}r} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] 1 & -2 & 1 \\[3pt] 3 & 1 & -1 \end{array}\right| =\mathbf{i}+4\mathbf{j}+7\mathbf{k}
The vector \mathbf{D} gives the direction of the line. We can find a point on the line by locating any point common to both planes. For example, if z=0, then x-2y=-1 and 3x+y=4. Solving these equations simultaneously, we find x=1 and y=1. So, the point (1,1,0) is on the line, and symmetric equations of the line of intersection are \dfrac{x-1}{1}=\dfrac{y-1}{4}=\dfrac{z}{7}
NOTE
We did not have to choose z=0; a value could have been assigned to any of the variables and the resulting two equations solved. Different choices would give equivalent equations of the line.
NOW WORK
7 Find the Distance from a Point to a PlanePrinted Page 739
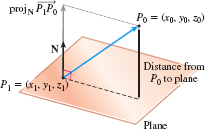
To find the distance from a point P_{0} to a plane, we use projections. As Figure 57 illustrates, if P_{1} is a point on a plane with a normal vector \mathbf{N}, then the distance from P_{0} to the plane is the magnitude of the projection of \overrightarrow{P_{1}~P_{0}} onto \mathbf{N}.
Suppose a plane is given by the general equation Ax+By+Cz=D
A normal vector \mathbf{N} to the plane is \mathbf{N}= A\mathbf{i}+ B\mathbf{j}+ C\mathbf{k}
740
The distance from the point P_{0}=(x_{0},y_{0},z_{0}) to the plane is \left[ \begin{array}{l} \hbox{Distance from} \\[0pt] P_{0} \hbox{ to the plane} \end{array} \right] =\left\Vert \hbox{proj}_{\mathbf{N}}\,\overrightarrow{P_{1}~P_{0}} \right\Vert =\frac{\left\vert \overrightarrow{P_{1}~P_{0}}\,{\cdot}\, \mathbf{N} \right\vert }{\left\Vert \,\mathbf{N}\right\Vert }
where P_{1}=(x_{1},y_{1},z_{1}) is a point on the plane.
Since \overrightarrow{P_{1}~P_{0}}=(x_{0}-x_{1})\mathbf{i}+(y_{0}-y_{1})\,\mathbf{ j}+(z_{0}-z_{1})\mathbf{k}, then \begin{eqnarray*} \left[ \begin{array}{l} \hbox{Distance from} \\ P_{0} \hbox{ to the plane} \end{array} \right] &=&\dfrac{\left\vert\,A(x_{0}-x_{1})+B(y_{0}-y_{1})+C(z_{0}-z_{1})\right\vert }{\sqrt{A^{2}+B^{2}+C^{2}}}\\ &=&\dfrac{\left\vert\,(Ax_{0}+By_{0}+Cz_{0})-(Ax_{1}+By_{1}+Cz_{1})\right\vert }{\sqrt{A^{2}+B^{2}+C^{2}}}\\ &\underset{\underset{\underset{\color{#0066A7}{\hbox{\(Ax_{1}+By_{1}+Cz _{1} =D\)}}}{\color{#0066A7}{\hbox{\(P_{1}\) is on the plane, so}}}}{\color{#0066A7}{\uparrow}}} {=}&\dfrac{|Ax_{0}+By_{0}+Cz_{0}-D|}{\sqrt{A^{2}+B^{2}+C^{2}}} \end{eqnarray*}
THEOREM Distance from a Point to a Plane
The distance d from the point P_{0}=(x_{0},y_{0},z_{0}) to the plane Ax+By+Cz=D is \bbox[5px, border:1px solid black, #F9F7ED]{ d=\dfrac{\left\vert \,Ax_{0}+By_{0}+Cz_{0}-D\,\right\vert }{\sqrt{A^{2}+B^{2}+C^{2}}}}\tag {1}
EXAMPLE 10Finding the Distance from a Point to a Plane
Find the distance d from the point ( 2,3,-1) to the plane x+4y+z=5.
Solution We use (1) with A=1, B=4, C=1, D=5, and P_{0}=(2,3,-1). Then d=\frac{\left\vert (1)(2)+(4)(3)+(1)(-1)-5\right\vert }{\sqrt{1+16+1}}= \frac{8}{3\sqrt{2}}=\frac{4\sqrt{2}}{3}
NOW WORK
EXAMPLE 11Finding the Distance Between Two Parallel Planes
Find the distance d between the parallel planes p_{1}:\ 2x+3y-z=3 \quad \hbox{and}\quad p_{2}: \ 2x+3y-z=4
Solution The planes p_{1} and p_{2} are parallel because \mathbf{N}_{1}=2\mathbf{i}+3\mathbf{j}-\mathbf{k}=\mathbf{N}_{2} and D_{1}=3 is not equal to D_{2}=4.
We find the distance between the planes by choosing a point on one plane and using the formula for distance from that point to the other plane. A point on p_{1} can be found by letting x=0 and y=0. Then z=-3, and ( 0,0,-3) is a point on p_{1}. The distance d from the point ( 0,0,-3) to the plane p_{2} is d=\dfrac{\left\vert \,2(0) +3(0) -1 (-3) -4\,\right\vert }{\sqrt{2^{2}+3^{2}+(-1) ^{2}}}=\dfrac{1}{\sqrt{ 14}}=\dfrac{\sqrt{14}}{14}