9.1 Parametric EquationsPrinted Page 637
637
The graph of an equation of the form y=f(x), where f is a function, is intersected no more than once by any vertical line. There are many graphs, however, such as circles and some parabolas, that do not pass the Vertical-line Test. To study such graphs requires a different model. One such model uses a pair of equations and a third variable, called a parameter.
DEFINITION
Suppose x=x(t) and y=y(t) are two functions of a third variable t, called the parameter, that are defined on the same interval I. Then the equations \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ x=x(t)\qquad y=y(t) }}
where t is in I are called parametric equations, and the collection of points defined by \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ (x,y) =( x( t) ,y( t) ) }}
is called a plane curve.
1 Graph Parametric EquationsPrinted Page 637
Parametric equations are particularly useful for describing motion along a curve. Suppose an object moves along a curve represented by the parametric equations \begin{equation*} x=x( t) \qquad y=y( t) \end{equation*}
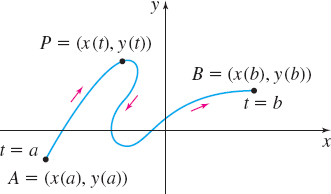
where each function is defined over the interval a\leq t\leq b. For a given value of t, the values of x=x( t) and y=y( t) determine a point ( x, y) on the curve. In fact, as t varies over the interval from t=a to t=b, successive values of t determine the direction of the motion of the object moving along the curve. See Figure 1. The arrows show the direction, or the orientation, of the object as it moves from A to B.
| t | x | y | (x,y) |
|---|---|---|---|
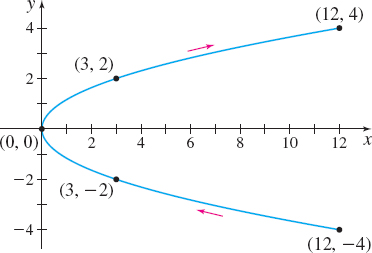
| -2 | 12 | -4 | (12,-4) |
| -1 | 3 | -2 | (3,-2) |
| 0 | 0 | 0 | (0,0) |
| 1 | 3 | 2 | (3,2) |
| 2 | 12 | 4 | (12,4) |
EXAMPLE 1Graphing a Plane Curve
Graph the plane curve represented by the parametric equations \begin{equation*} x( t) =3t^{2} \qquad y( t) =2t\;-2\leq t\leq 2 \end{equation*}
Indicate the orientation of the curve.
Solution Corresponding to each number t, -2\leq t\leq 2, there are a number x and a number y that are the coordinates of a point ( x,y) on the curve. We form a table listing various choices of the parameter t and the corresponding values for x and y, as shown in Table 1.
The motion begins when t=-2 at the point ( 12,-4) and ends when t=2 at the point ( 12,4). Figure 2 illustrates the plane curve whose parametric equations are x( t) =3t^{2} and y( t) =2t. The arrows indicate the orientation of the plane curve for increasing values of the parameter t.
2 Find a Rectangular Equation for a Curve Represented ParametricallyPrinted Page 638
638
The plane curve in Figure 2 should look familiar. To identify it, we find the corresponding rectangular equation by eliminating the parameter t from the parametric equations \begin{equation*} x( t) =3t^{2}\qquad y( t) =2t\quad -2\leq t\leq 2 \end{equation*}
We begin by solving for t in y=2t, obtaining t=\dfrac{y}{2}. Then we substitute t =\dfrac{y}{2} in the other equation. \begin{equation*} x=3t^{2}=3\left( \dfrac{y}{2}\right) ^{2}=\dfrac{3y^{2}}{4} \end{equation*}
The equation x=\dfrac{3y^{2}}{4} is a parabola with its vertex at the origin and its axis of symmetry along the x-axis. We refer to this equation as the rectangular equation of the curve to distinguish it from the parametric equations.
Notice that the plane curve represented by the parametric equations x( t) =3t^{2}, y( t) =2t, -2\leq t\leq 2, is only part of the parabola x=\dfrac{3y^{2}}{4}. In general, the graph of the rectangular equation obtained by eliminating the parameter will contain more points than the plane curve defined using parametric equations. Therefore, when graphing a plane curve represented by a rectangular equation, we may have to restrict the graph to match the parametric equations.
EXAMPLE 2Finding a Rectangular Equation for a Plane Curve Represented Parametrically
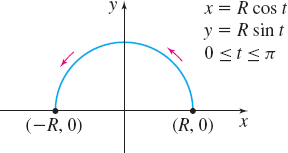
Find a rectangular equation of the curve whose parametric equations are \begin{equation*} x( t) =R\, \cos t \qquad y( t) =R\, \sin t \end{equation*}
where R>0 is a constant. Graph the plane curve and indicate its orientation.

Solution The presence of the sine and cosine functions in the parametric equations suggests using the Pythagorean Identity \cos ^{2}t+\sin ^{2}t=1. Then \begin{array}{rcl@{\quad}crcl} \left( \dfrac{x}{R}\right) ^{2}+\left( \dfrac{y}{R}\right) ^{2}& =&1 &\qquad\color{#0066A7}{\cos \;t = \tfrac{x}{R}\quad \sin t=\dfrac{y}{R}}\\ x^{2}+y^{2}& =& R^{2} \end{array}
The graph of the rectangular equation is a circle with center at the origin and radius R. In the parametric equations, as the parameter t increases, the points (x,y) on the circle are traced out in the counterclockwise direction, as shown in Figure 3.
NOW WORK
When analyzing the parametric equations in Example 2, notice there are no restrictions on t, so t varies from -\infty to \infty . As a result, the circle is repeated each time t increases by 2\pi.
If we wanted to describe a curve consisting of exactly one revolution in the counterclockwise direction, the domain must be restricted to an interval of length 2\pi. For example, we could use \begin{equation*} x( t) =R\, \cos t\qquad y( t) =R\, \sin t\qquad 0\leq t\leq 2\pi \end{equation*}
Now the plane curve starts when t=0 at (R,0) and ends when t=2\pi at (R, 0).
If we wanted the curve to consist of exactly three revolutions in the counterclockwise direction, the domain must be restricted to an interval of length 6\pi. For example, we could use x( t) =R\, \cos t, y( t) =R\, \sin t, with -2\pi \leq t\leq 4\pi, or 0\leq t\leq 6\pi, or 2\pi \leq t\leq 8\pi, or any arbitrary interval of length 6\pi .
639
EXAMPLE 3Finding a Rectangular Equation for a Plane Curve Represented Parametrically
Find rectangular equations for the plane curves represented by each of the parametric equations. Graph each curve and indicate its orientation.
(a) x( t) =R\, \cos t\quad y( t) = R\, \sin t\quad 0\leq t\leq \pi and R> 0
(b) x( t) =R\, \sin t\quad y( t) = R\, \cos t\quad 0\leq t\leq \pi and R> 0
Solution (a) We eliminate the parameter t using a Pythagorean Identity. \begin{eqnarray*} \cos^{2}t+\sin ^{2}t &=&1 \\ \left( \dfrac{x}{R}\right) ^{2}+\left( \dfrac{y}{R}\right) ^{2} &=&1 \qquad \color{#0066A7}{\cos t=\dfrac{x}{R},\quad \sin t=\dfrac{y}{R}} \\ x^{2}+y^{2} &=&R^{2} \tag{1} \end{eqnarray*}
The rectangular equation represents a circle with radius R and center at the origin. In the parametric equations, 0\leq t\leq \pi, so the curve begins when t=0 at the point ( R, 0) , passes through the point ( 0, R) when t=\dfrac{\pi }{2}, and ends when t=\pi at the point ( -R,0). The curve is an upper semicircle of radius R with counterclockwise orientation, as shown in Figure 4. If we solve equation (1) for y, we obtain the rectangular equation of the semicircle y=\sqrt{R^{2}-x^{2}}\qquad\hbox{where }-R\leq x\leq R
(b) We eliminate the parameter t as we did in (a), and again we obtain \begin{eqnarray*} x^{2}+y^{2}=R^{2}\tag{2} \end{eqnarray*}

The rectangular equation represents a circle with radius R and center at ( 0,0) . But in the parametric equations, 0\leq t\leq \pi , so now the curve begins when t=0 at the point ( 0, R), passes through the point ( R, 0) when t=\dfrac{\pi }{2}, and ends at the point \left( 0,-R\right) when t=\pi. The curve is a right semicircle of radius R with a clockwise orientation, as shown in Figure 5. If we solve equation (2) for x, we obtain the rectangular equation of the semicircle x=\sqrt{R^{2}-y^{2}}\qquad \hbox{where }-R\leq y\leq R
Parametric equations are not unique; that is, different parametric equations can represent the same graph. Two examples of other parametric equations that represent the graph in Figure 5 are
- x( t) =R\, \sin t \qquad y( t) =-R\, \cos (\pi -t)\quad 0\leq t\leq \pi
- x( t) =R\, \sin ( 3t)\;y( t) =R\, \cos ( 3t) \qquad\,\,\,\, 0\leq t\leq \dfrac{\pi }{3}
NOTE
In Example 3 (a) we expressed the rectangular equation as a function y=f ( x), and in (b) we expressed the rectangular equation as a function x=g (y).
There are other examples.
NOW WORK
640
EXAMPLE 4Finding a Rectangular Equation for a Plane Curve Represented Parametrically
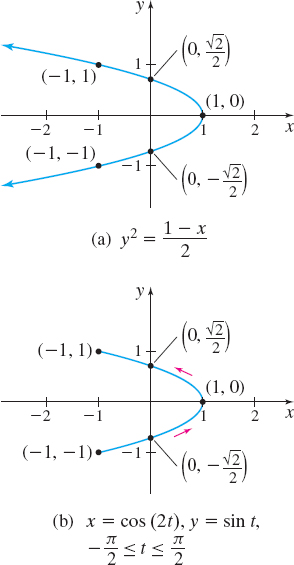
(a) Find a rectangular equation of the plane curve whose parametric equations are x( t) =\cos ( 2t) \qquad y( t) =\sin t\quad -\dfrac{\pi }{2}\leq t\leq \dfrac{\pi }{2}
(b) Graph the rectangular equation.
(c) Determine the restrictions on x and y so the graph corresponding to the rectangular equation is identical to the plane curve described by x=x( t)\qquad y=y( t)\quad -\dfrac{\pi }{2} \leq t\leq\dfrac{\pi}{2}
(d) Graph the plane curve whose parametric equations are x=\cos ( 2t)\qquad y=\sin t\quad -\dfrac{\pi }{2}\leq t\leq \dfrac{\pi }{2}
Solution (a) To eliminate the parameter t, we use a trigonometric identity that involves \sin t and \cos ( 2t), namely, \sin ^{2}t=\dfrac{1-\cos ( 2t) }{2}. Then \begin{equation*} y^{2}\underset{\color{#0066A7}{\underset{\hbox{\(y( t) =\sin t\)}}{{\uparrow }}}}{=}\sin ^{2}t=\dfrac{1-\cos (2t) }{2}\underset{\color{#0066A7}{\underset{\hbox{\(x( t)=\cos ( 2t)\)}}{{\uparrow }}}}{=}\dfrac{1-x}{2}\\ \end{equation*}
(b) The curve represented by the rectangular equation y^{2}=\dfrac{1-x}{2} is the parabola shown in Figure 6(a).
(c) The plane curve represented by the parametric equations does not include all the points on the parabola. Since x( t) =\cos ( 2t) and -1\leq \cos ( 2t) \leq 1, then -1\leq x\leq 1. Also, since y( t) =\sin t, then -1\leq y\leq 1. Finally, the curve is traced out exactly once in the counterclockwise direction from the point ( -1,-1) (when t=-\dfrac{\pi }{2}) to the point ( -1,1) (when t=\dfrac{\pi }{2}).
(d) The plane curve represented by the given parametric equations is the part of the parabola shown in Figure 6(b).
NOW WORK
3 Use Time as the Parameter in Parametric EquationsPrinted Page 640
If the parameter t represents time, then the parametric equations x=x(t) and y=y(t) specify how the x- and y-coordinates of a moving object vary with time. This motion is sometimes referred to as curvilinear motion. Describing curvilinear motion using parametric equations specifies not only where the object is, that is, its location ( x, y) , but also when it is there, that is, the time t. A rectangular equation provides only the location of the object.
EXAMPLE 5Using Time as the Parameter in Parametric Equations
Describe the motion of an object that moves along a curve so that at time t it has coordinates \begin{equation*} x( t) =3\cos t\qquad y( t) =4\sin t \qquad 0\leq t\leq 2\pi \end{equation*}
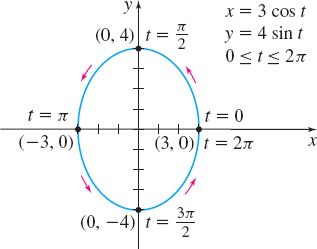
Solution We eliminate the parameter t using the Pythagorean Identity \cos ^{2}t+\sin ^{2}t=1. \begin{equation*} \frac{x^{2}}{9}+\frac{y^{2}}{16}=1\qquad \color{#0066A7}{\cos t= \dfrac{x}{3}, \sin t= \dfrac{y}{4}} \end{equation*}
The plane curve is the ellipse shown in Figure 7. When t=0, the object is at the point (3,0). As t increases, the object moves around the ellipse in a counterclockwise direction, reaching the point (0,4) when t=\dfrac{ \pi }{2}, the point (-3,0) when t=\pi, the point (0,-4) when t= \dfrac{3\pi }{2}, and returning to its starting point \left( 3,0\right) when t=2\pi.
641
NOW WORK
4 Convert a Rectangular Equation to Parametric EquationsPrinted Page 641
Suppose the rectangular equation corresponding to a curve is known. Then the curve can be represented by a variety of parametric equations.
For example, if a curve is defined by the function y=f( x), one way of obtaining parametric equations is to let x=t. Then y=f( t) and \begin{equation*} x(t) =t\qquad y(t) =f t) \end{equation*}
where t is in the domain of f, are parametric equations of the curve.
EXAMPLE 6Finding Parametric Equations for a Curve Represented by a Rectangular Equation
Find parametric equations corresponding to the equation y=x^{2}-4.
Solution We let x=t. Then parametric equations are x( t) =t\qquad y( t) =t^{2}-4\qquad -\infty < t < \infty
We can also find parametric equations for y=x^{2}-4 by letting x=t^{3}. Then the parametric equations are \begin{equation*} x( t) =t^{3}\qquad y( t) =t^{6}-4\quad -\infty < t < \infty \end{equation*}
Although the choice of x may appear arbitrary, we need to be careful when choosing the substitution for x. The substitution must be a function that allows x to take on all the values in the domain of f. For example, if we let x( t) =t^{2}, then y( t) =t^{4}-4. But x( t) =t^{2}, y( t) =t^{4}-4 are not parametric equations for all of y=x^{2}-4, since only points for which x\geq 0 are obtained.
NOW WORK
EXAMPLE 7Finding Parametric Equations for an Object in Motion
Find parametric equations that trace out the ellipse \begin{equation*} \frac{x^{2}}{4}+y^{2}=1 \end{equation*}
where the parameter t is time (in seconds) and:
(a) The motion around the ellipse is counterclockwise, begins at the point (2,0), and requires 1 second for a complete revolution.
(b) The motion around the ellipse is clockwise, begins at the point (0,1) , and requires 2 seconds for a complete revolution.
Solution (a) Figure 8 shows the graph of the ellipse \dfrac{ x^{2}}{4}+y^{2}=1.

Since the motion begins at the point ( 2,0), we want x=2 and y=0 when t=0. We let \begin{equation*} x( t) =2\cos ( \omega t) \qquad\hbox{and}\qquad y( t) =\sin ( \omega t) \end{equation*}
for some constant \omega. This choice for x=x( t) and y=y( t) satisfies the equation \dfrac{x^{2}}{4}+y^{2}=1 and also satisfies the requirement that when t=0, then x=2 and y=0.
642
For the motion to be counterclockwise, as t increases from 0, the value of x must decrease and the value of y must increase. This requires \omega > 0. [Do you see why? If \omega > 0, then x=2\cos ( \omega t) is decreasing when t > 0 is near zero, and y=\sin ( \omega t) is increasing when t > 0 is near zero.]
Finally, since 1 revolution takes 1 second, the period is \dfrac{2\pi }{ \omega }=1, so \omega =2\pi. Parametric equations that satisfy the conditions given in (a) are \begin{equation*} x( t) =2\cos ( 2\pi t) \qquad y( t) =\sin ( 2\pi t)\;0\leq t\leq 1 \end{equation*}
(b) Figure 9 shows the graph of the ellipse \dfrac{x^{2}}{4}+y^{2}=1.
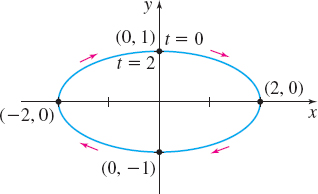
Since the motion begins at the point ( 0,1) , we want x=0 and y=1 when t=0. We let \begin{equation*} x( t) =2\sin ( \omega t) \qquad \hbox{and}\qquad y( t) =\cos ( \omega t) \end{equation*}
for some constant \omega. This choice for x=x( t) and y=y( t) satisfies the equation \dfrac{x^{2}}{4}+y^{2}=1 and also satisfies the requirement that when t=0, then x=2\sin 0=0 and y=\cos 0=1.
For the motion to be clockwise, as t increases from 0, the value of x must increase and the value of y must decrease. This requires that \omega > 0.
Finally, since 1 revolution takes 2 seconds, the period is \dfrac{2\pi }{ \omega }=2, or \omega =\pi. Parametric equations that satisfy the conditions given in (b) are x( t) =2\sin ( \pi t) \qquad y( t) =\cos ( \pi t)\;0\leq t\leq 2
NEED TO REVIEW?
The period of a sinusoidal graph is discussed in Section P.6, p. 50.
NOW WORK
The Cycloid
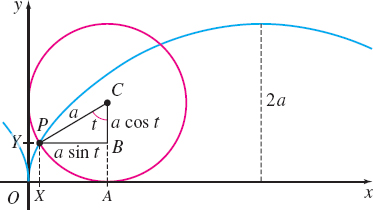
Suppose that a circle rolls along a horizontal line without slipping. As the circle rolls along the line, a point P on the circle traces out a curve called a cycloid, as shown in Figure 10. Deriving the equation of the cycloid in rectangular coordinates is complicated, but the derivation in terms of parametric equations is relatively easy.
We begin with a circle of radius a. Suppose the fixed line on which the circle rolls is the x-axis. Let the origin be one of the points at which the point P comes into contact with the x-axis. Figure 10 shows the position of this point P after the circle has rolled a bit. The angle t (in radians) measures the angle through which the circle has rolled. Since the circle does not slip, it follows that \hbox{Arc }AP=d( O , A)
The length of the arc AP is a t=d ( O,A) \qquad {\color{#0066A7}{s=r\theta ,\;r=a,\quad \theta =t}}
The x-coordinate of the point P=( x,y) is x=d( O,X) =d ( O,A) -d( X,A) =at-a\sin t=a(t-\sin t)
The y-coordinate of the point P is y=d( O,Y) =d( A,C) -d( B,C) =a-a\cos t=a(1-\cos t)
RECALL
For a circle of radius r, a central angle of \theta radians subtends an arc whose length s is s=r\, \theta.
THEOREM Parametric Equations of a Cycloid
Parametric equations of a cycloid are \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ x( t) =a(t-\sin t)\qquad y( t) =a(1-\cos t)\quad -\infty < t < \infty }}
643
Applications to Mechanics
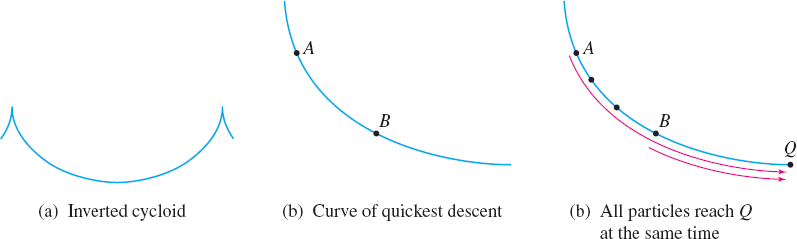
If a < 0 in the parametric equations of the cycloid, the result is an inverted cycloid, as shown in Figure 11(a). The inverted cycloid arises as a result of some remarkable applications in the field of mechanics. We discuss two of them: the brachistochrone and tautochrone.
NOTE
In Greek, brachistochrone means “the shortest time,” and tautochrone “equal time.”
The brachistochrone is the curve of quickest descent. If an object is constrained to follow some path from a point A to a lower point B (not on the same vertical line) and is acted on only by gravity, the time needed to make the descent is minimized if the path is an inverted cycloid. See Figure 11(b). For example, in sliding packages from a loading dock onto a ship, a ramp in the shape of an inverted cycloid might be used so the packages get to the ship in the least amount of time. This discovery, which is attributed to many famous mathematicians (including Johann Bernoulli and Blaise Pascal), was a significant step in creating the branch of mathematics known as the calculus of variations.
Suppose Q is the lowest point on an inverted cycloid. If several objects placed at various positions on an inverted cycloid simultaneously begin to slide down the cycloid, they will reach the point Q at the same time, as indicated in Figure 11(c). This is referred to as the tautochrone property of the cycloid. It was used by the Dutch mathematician, physicist, and astronomer Christian Huygens (1629–1695) to construct a pendulum clock with a bob that swings along an inverted cycloid, as shown in Figure 12. In Huygens'clock, the bob was made to swing along an inverted cycloid by suspending the bob on a thin wire constrained by two plates shaped like cycloids. In a clock of this design, the period of the pendulum is independent of its amplitude.