Finding the \(\mathbf{k}\) Component of the Outer Unit Normal Vectors of an \(xy\,\)-Simple Surface

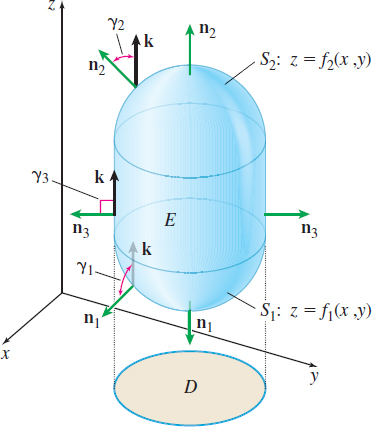
Consider the surface \(S\) with positive orientation that forms the boundary of the closed, bounded solid \(E\) shown in Figure 61. Notice that the surface \(S\) can be decomposed into three surfaces, \(S_{1},\) \(S_{2},\) and \(S_{3}\), and that each of the outer unit normal vectors \(\mathbf{n}_{1},\) \(\mathbf{n}_{2}\), and \(\mathbf{n}_{3}\) of the three surfaces points away from the solid \(E\) enclosed by \(S\).

Assume the surfaces \(S_{1}\) and \(S_{2}\) are defined by the equations \[ \begin{equation*} S_{1}{:}\quad z=f_{1}(x,y)\qquad \hbox{and}\qquad S_{2}{:}\quad z=f_{2}(x,y) \end{equation*} \]

where \(f_{1}(x,y)<f_{2}(x,y)\) on \(D,\) the functions \(f_{1}\) and \(f_{2}\) are continuous on \(D\), and both \(f_{1}\) and \(\ f_{2}\) have continuous partial derivatives on \(D\). The surface \(S_{3}\) is the portion of a cylindrical surface between \(S_{1}\) and \(S_{2}\) formed by lines parallel to the \(z\)-axis and along the boundary of \(D\). The solid \(E\) is enclosed by \(S_{2}\) on the top, \(S_{1}\) on the bottom, and the lateral surface \(S_{3}\) on the sides. A surface \(S\) with these properties is called \(\boldsymbol x\)\(\boldsymbol y\)-simple.

Find the \(\mathbf{k}\) component of the outer unit normal vectors of \(S\).

Solution For the top surface \(S_{2}\): \(z=f_{2}(x,y)\), the outer unit normal vector \(\mathbf{n}_{2}\) is the same as the upward-pointing unit normal vector to \(S_{2}\). \[ \begin{equation*} \mathbf{n}_{2}=\dfrac{-(f_{2})_x(x,y)\mathbf{i}-(f_{2})_ y(x,y)\mathbf{j}+\mathbf{k} }{\sqrt{[(f_{2})_x(x,y)]^{2}+[(f_{2})_y(x,y)]^{2}+1}} \end{equation*} \]

The \(\mathbf{k}\) component of \(\mathbf{n}_{2}\) is given by the direction cosine \(\cos \gamma _{2}\), where \[ \cos \gamma _{2}=\mathbf{n}_{2}\,{\cdot}\, \mathbf{k}=\dfrac{1}{\sqrt{ [(f_{2})_x(x,y)]^{2}+[(f_{2})_y(x,y)]^{2}+1}} \]

1033

For the bottom surface \(S_{1}\): \(z=f_{1}(x,y)\), the outer unit normal vector \(\mathbf{n}_{1}\) equals the downward-pointing unit normal vector \(-\mathbf{n}\) to \(S_{1}\). \[ \begin{equation*} \mathbf{n}_{1}=-\mathbf{n}=\dfrac{(f_{1})_{x}(x,y)\mathbf{i}+(f_{1})_y(x,y)\mathbf{j}- \mathbf{k}}{\sqrt{[(f_{1})_x(x,y)]^{2}+[(f_{1})_y(x,y)]^{2}+1}} \end{equation*} \]

The \(\mathbf{k}\) component of \(\mathbf{n}_{1}\) is given by the direction cosine \(\cos \gamma _{1}\), where \[ \cos \gamma _{1}=\mathbf{n}_{1}\,{\cdot}\, \mathbf{k}=\dfrac{-1}{\sqrt{[(f_{1})_x(x,y)]^{2}+[(f_{1})_y(x,y)]^{2}+1}} \]

For the lateral surface \(S_{3}\), the outer unit normal vector \(\mathbf{n} _{3} \) is orthogonal to \(\mathbf{k}\) at each point on \(S_{3}\). The \(\mathbf{k }\) component of \(\mathbf{n}_{3},\) given by the direction cosine, \(\cos \gamma _{3}\), is therefore \(0\).