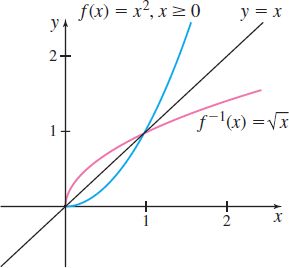Finding the Inverse of a Domain-Restricted Function

Find the inverse of \(f(x) = x^{2}\) if \(x\geq 0\).

Solution The function \(f(x) = x^{2}\) is not one-to-one (see Example 1(a)). However, by restricting the domain of \(f\) to \(x\geq 0\), the new function \(f\) is one-to-one, so \(f^{-1}\) exists. To find \(f^{-1}\), follow the steps.

Step 1  \(y=x^{2}\), where \(x\geq 0\).

Step 2  Interchange the variables \(x\) and \(y\): \(x = y^{2}\), where \(y\geq 0\). This is the inverse function written implicitly.

Step 3  Solve for \(y\): \(y=\sqrt{x}=f^{-1}(x)\). (Since \(y\geq 0\), only the principal square root is obtained.)

Step 4  Check that \(f^{-1}(x) = \sqrt{x}\) is the inverse function of \(f\). \[ \begin{array}{rcl@{\qquad}l} f^{-1}( f( x))~&=&\sqrt{f( x) }=\sqrt{x^{2}}=\vert x\vert =x, & \hbox{where }x\geq 0 \\[2pt] f( f^{-1}( x))~&=&[ f^{-1}( x) ] ^{2}=[ \sqrt{x}] ^{2}=x, & \hbox{where }x\geq 0 \end{array} \]