Solving Inequalities

Solve each inequality and graph the solution:

(a) \(4x+7\geq 2x-3\)

(b) \(x^{2}-4x+3>0\)

(c) \(x^{2}+x+1 < 0\)

(d) \(\dfrac{1+x}{1-x}>0\)

Solution (a) \[ \begin{array}{@{\hspace*{-4pt}}rcll@{\quad}l} 4x+7&\geq& 2x-3 & & \\ 4x&\geq& 2x-10 & & {\color{#0066A7}{\hbox{Subtract 7 from both sides.}}} \\ 2x&\geq& -10 & & {\color{#0066A7}{\hbox{Subtract 2\(x\) from both sides.}}} \\ x&\geq& -5 & & {\color{#0066A7}{\hbox{Divide both sides by 2.}}}\quad \\ &&&&{\color{#0066A7}{\hbox{(The direction of the inequality symbol is unchanged.)}}} \end{array} \]

image
Figure 1 \(x\geq 5\)

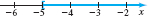
The solution using interval notation is \([ -5,\infty ) \). See Figure 1 for the graph of the solution.

The test number can be any real number in the interval, but it cannot be an endpoint.

(b) This is a quadratic inequality. The related quadratic equation \(x^{2}-4x+3= ( x-1) ( x-3) =0\) has two solutions, \(1\) and \(3\). We use these numbers to partition the number line into three intervals. Now select a test number in each interval, and determine the value of \(x^{2}-4x+3\) at the test number. See Table 2.

Table 2

Interval Test Number Value of \({x^{2}-4x}+{3}\) Sign of \({x^{2}-4x}+ {3}\)
\( ( -\infty ,1)\)\({0}\)\({3}\)Positive
\( (1,3)\)\({2}\)\({-1}\)Negative
\(( 3,\infty )\)\({4}\)\({3}\)Positive
image
Figure 2 \(x<1\) or \(x>3\)

We conclude that \(x^{2}-4x+3>0\) on the set \(( -\infty ,1) \cup ( 3,\infty) \). See Figure 2 for the graph of the solution.

(c) The quadratic equation \(x^{2}+x+1=0\) has no real solution, since its discriminant is negative. [See Example 4(b)]. When this happens, the quadratic inequality is either positive for all real numbers or negative for all real numbers. To see which is true, evaluate \(x^{2}+x+1\) at some number, say, \(0\). At \(0,\) \(x^{2}+x+1=1,\) which is positive. So, \(x^{2}+x+1>0\) for all real numbers \(x\). The inequality \(x^{2}+x+1 < 0\) has no solution.

(d) The only solution of the rational equation \(\dfrac{1+x}{1-x} =0\) is \(x=-1;\) also, the expression \(\dfrac{1+x}{1-x}\) is not defined for \(x=1.\) We use the solution \(-1\) and the value \(1\), at which the expression is undefined, to partition the real number line into three intervals. Now select a test number in each interval, and evaluate the rational expression \(\dfrac{1+x}{1-x}\) at each test number. See Table 3.

Table 3

Interval Test Number Value of \(\dfrac{{1}+{x}}{{1}-{x}}\) Sign of \(\dfrac{{1}+{x}}{{1}-{x}}\)
\(( {-\infty ,-1})\) \({-2}\) \({-}\dfrac{1}{3}\) Negative
\(( -{1,1})\) \({0}\) \({1}\) Positive
\(( 1{,\infty })\) \({2}\) \(-3\) Negative
image
Figure 3 \(-1<x<1\)

We conclude that \(\dfrac{1+x}{1-x}>0\) on the interval \(( -1,1)\). See Figure 3 for the graph of the solution.