Estimating the Error in Using the Trapezoidal Rule

Estimate the error that results from using the Trapezoidal Rule with \(n=4\) and with \(n=6\) to approximate \( \int_{1}^{2}\dfrac{e^{x}}{x}dx\). See Example 2.

A CAS can be used to find \(f{^\prime{^\prime}} (x)\).

Solution To estimate the error resulting from approximating \( \int_{1}^{2}\dfrac{e^{x}}{x}dx\) using the Trapezoidal Rule, we need to find the absolute maximum value of \(\vert f^{\prime \prime}\vert\) on the interval \([ 1,2] .\) We begin by finding \(f^{\prime \prime}\): \[ \begin{eqnarray*} f( x) &=&\dfrac{e^{x}}{x} \\[5pt] f^{\prime} (x) &=&\dfrac{d}{dx}\dfrac{e^{x}}{x}=\dfrac{xe^{x}-e^{x}}{x^{2}}= \dfrac{e^{x}}{x}-\dfrac{e^{x}}{x^{2}} \\[5pt] f^{\prime \prime} (x) &=&\dfrac{d}{dx}\left( \dfrac{e^{x}}{x}-\dfrac{e^{x}}{ x^{2}}\right) =\dfrac{d}{dx}\dfrac{e^{x}}{x}-\dfrac{d}{dx}\dfrac{e^{x}}{x^{2} }=\left( \dfrac{e^{x}}{x}-\dfrac{e^{x}}{x^{2}}\right) -\dfrac{ e^{x}x^{2}-2e^{x}x}{x^{4}}\\[5pt] &=&\dfrac{e^{x}}{x}-\dfrac{e^{x}}{x^{2}}-\dfrac{e^{x} }{x^{2}}+\dfrac{2e^{x}}{x^{3}} \\[5pt] &=&e^{x}\left( \dfrac{1}{x}-\dfrac{2}{x^{2}}+\dfrac{2}{x^{3}}\right) \end{eqnarray*} \]

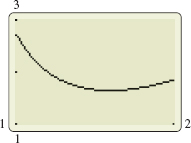
Since \(\vert f^{\prime \prime}\vert\) is continuous on the interval \([1,2] ,\) the Extreme Value Theorem guarantees that \( \vert f^{\prime \prime}\vert\) has an absolute maximum on \([1,2]\). We find the absolute maximum of \(\vert f^{\prime \prime}\vert\) using graphing technology. As seen from Figure 17, the absolute maximum is at the left endpoint \(1.\) The absolute maximum value of \(f^{\prime \prime}\) is \(\left\vert e^{1}\left( \dfrac{1}{1}-\dfrac{ 2}{1^{2}}+\dfrac{2}{1^{3}}\right) \right\vert =e.\) So, \(M=e\).

Figure 17 The absolute maximum of \(\vert f^{\prime\prime} \vert\) on \([1,2 ]\) is at \(x=1.\)

When \(n=4,\) the error in using the Trapezoidal Rule is \[ \hbox{Error} \leq \dfrac{( b-a) ^{3}M}{12n^{2}}=\dfrac{(2-1)^{3}(e) }{(12)(4^{2})}=\dfrac{e}{192}\approx 0.014 \]

That is, \[ \begin{eqnarray*} 3.069-0.014 & \leq &\int_{1}^{2}\dfrac{e^{x}}{x}dx \leq 3.069+0.014 \\[5pt] 3.055 & \leq &\int_{1}^{2}\dfrac{e^{x}}{x}dx \leq 3.083 \end{eqnarray*} \]

513

When \(n=6,\) the error in using the Trapezoidal Rule is \[ \hbox{Error} \leq \dfrac{\left( b-a\right) ^{3}M}{12n^{2}}=\dfrac{(2-1)^{3}(e) }{(12)(6^{2})}=\dfrac{e}{432}\approx 0.006 \]

That is, \[ \begin{eqnarray*} 3.063-0.006 & \leq &\int_{1}^{2}\dfrac{e^{x}}{x}dx \leq 3.063+0.006 \nonumber \\[5pt] 3.057 & \leq &\int_{1}^{2}\dfrac{e^{x}}{x}dx \leq 3.069 \end{eqnarray*} \]