Estimating the Error in Using Simpson's Rule

Estimate the error that results from using Simpson's Rule with \(n =4\) to approximate \( \int_{\pi }^{2\pi }\frac{\sin x}{x}dx\). (See Example 6.)

Solution To estimate the error, we need to find the absolute maximum value of \(\vert f^{(4) }\vert\) on the interval \([\pi ,2\pi ]\). We begin by finding \(f^{(4) }\): \[ \begin{eqnarray*} f(x) &=&\dfrac{\sin x}{x} \\[5pt] f^{\prime} (x) &=&\frac{x\cos x-\sin x}{x^{2}}=\frac{\cos x}{x}-\frac{\sin x}{x^{2}} \\ && \\ f^{\prime \prime} (x) &=&\left[ \frac{-x\sin x-\cos x}{x^{2}} \right] -\left[ \frac{x^{2}\cos x-2x\sin x}{x^{4}}\right]\\[6pt] & = & \frac{2 \sin x}{x^{3}} -\frac{\sin x}{x}-\frac{2\cos x}{x^{2}} \\[15pt] f^{\prime \prime \prime} (x) &=&\left[ \frac{2x^{3}\cos x-6x^{2}\sin x}{x^{6}}\right] -\left[ \frac{x\cos x-\sin x}{x^{2}}\right] - \left[ \frac{-2x^{2}\sin x-4x\cos x}{x^{4}}\right] \\[6pt] &=&\frac{2\cos x}{x^{3}}-\frac{6\sin x}{x^{4}}-\frac{\cos x}{x}+\frac{ \sin x}{x^{2}}+\frac{2\sin x}{x^{2}}+\frac{4\cos x}{x^{3}}\\[6pt] &=&\frac{6 \cos x}{x^{3}}-\frac{\cos x}{x}+\frac{3 \sin x}{x^{4}} \\[6pt] && \\ f^{\,(4) }(x) &=&\left[ \frac{-6x^{3}\sin x-18x^{2}\cos x}{ x^{6}}\right] -\left[ \frac{-x\sin x-\cos x}{x^{2}}\right] \\[8pt] &&+\,\left[ \frac{3x^{2}\cos x-6x\sin x}{x^{4}}\right] -\left[ \frac{6x^{4}\cos x-24x^{3}\sin x}{x^{8}}\right] \\[8pt] &=&\frac{4 \cos x}{x^{2}}-\frac{24 \cos x}{x^{4}}+\frac{\sin x}{x}-\frac{ 12 \sin x}{x^{3}}+\frac{24 \sin x}{x^{5}} \end{eqnarray*} \]

517

We use graphing technology to find the absolute maximum value of \(\vert f^{(4)}\vert\). See Figure 20.

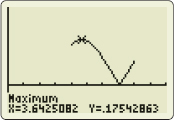
Since on the interval \([\pi ,2\pi]\) the maximum value of \(\vert f^{(4)}\vert \lt 0.176,\) we use \(M=0.176\). Then the error that results from using Simpson's Rule to approximate \(\int_{\pi }^{2\pi }\frac{\sin x}{x}dx\) is \[ \hbox{Error} \leq \frac{M(b-a)^{5}}{180n^{4}}=\frac{0.176(2\pi -\pi )^{5}}{180\cdot 4^{4}}\approx 0.001 \]

That is, \[ \begin{eqnarray*} -0.434-0.001 & \leq& \int_{\pi }^{2\pi }\frac{\sin x}{x}dx \leq -0.434+0.001 \\[5pt] -0.435 & \leq& \int_{\pi }^{2\pi }\frac{\sin x}{x}dx \leq -0.433 \end{eqnarray*} \]