13.1 Assess Your UnderstandingPrinted Page 871
Concepts and Vocabulary
True or False The directional derivative Duf(x0,y0) equals the rate of change of z=f(x,y) at (x0,y0) in the direction of the unit vector u.
True
True or False For a function z=f(x,y), the partial derivative fx(x0,y0) is the directional derivative at (x0,y0) in the direction of i.
True
True or False Both the directional derivative Duf(x,y) and the gradient ∇f(x,y) of a function z=f(x,y) are vectors.
False
872
True or False If z=f(x,y) is a differentiable function, then the directional derivative of f at (x0,y0) in the direction of u=cosθi+sinθj is given by Duf(x0,y0)=fx(x0,y0)cosθ+fy(x0,y0)sinθ.
True
True or False The vector xi+sinyj is the gradient of f(x,y)=xsiny.
False
The directional derivative Duf(x0,y0) of f at (x0,y0) is a maximum when u=_____.
1‖
The value of z=f(x,y) at (x_{0},y_{0}) decreases most rapidly in the direction of _____.
-\nabla f(x_0,y_0)
For a differentiable function z=f(x,y), the maximum value of D_{\mathbf{u}}f(x_{0},y_{0}) is _____.
\left\Vert{\nabla f(x_0 ,y_0 )} \right\Vert
Skill Building
In Problems 9–16,
- (a) Find the directional derivative of each function at the indicated point and in the indicated direction.
- (b) Interpret the result as a rate of change.
- (c) Interpret the result as a slope.
f(x,y)=xy^{2}+x^{2} at (-1,2) in the direction \mathbf{u}= \dfrac{1}{2}\mathbf{i}+\dfrac{\sqrt{3}}{2}\mathbf{j}
- (a) {D}_{\bf u} {f}( - 1, 2) = 1 - 2\sqrt 3 \approx - 2.46
- (b) Starting at the point (-1,2) and moving in the direction {\bf u} = \dfrac{1}{2}{\bf i} + \dfrac{\sqrt 3}{2}{\bf j}, the function is changing at a rate of approximately -2.46 units per unit length.
- (c) The slope of the tangent line to the curve C that is the intersection of the surface f(x, y) = {xy}^{2}+x^{2}, and the plane perpendicular to the xy-plane that contains the line through point (-1, 2, 0) in the direction {\bf u} = \dfrac{1}{2}{\bf i} + \dfrac{\sqrt 3 }{2}{\bf j}, is approximately -2.46.
f(x,y)=3xy+y^{2} at (2,1) in the direction \mathbf{u}= \dfrac{\sqrt{2}}{2}\mathbf{i}+\dfrac{\sqrt{2}}{2}\mathbf{j}
f(x,y)=2xy-y^{2} at (-1,3) in the direction \theta =\dfrac{2\pi }{3}
- (a) {D}_{\bf u} {f}( - 1, 3) = - 3 - 4\sqrt 3\approx - 9.93
- (b) Starting at the point (-1, 3) and moving in the direction \theta = \dfrac{2\pi}{3}, the function is changing at a rate of approximately -9.93 units per unit length.
- (c) The slope of the tangent line to the curve C that is the intersection of the surface f(x, y) = 2 xy - y^{2}, and the plane perpendicular to the xy-plane that contains the line through point (-1, 3, 0) in the direction \theta = \dfrac{2\pi}{3}, is approximately -9.93.
f(x,y)=2xy+x^{2} at (0,3) in the direction \theta = \dfrac{4\pi }{3}
f(x,y)=xe^{y}+ye^{x} at (0,0) in the direction \theta = \dfrac{\pi }{6}
- (a) {D}_{\bf u} {f}(0, 0) = {{1 + \sqrt 3} \over 2} \approx 1.37
- (b) Starting at the point (0, 0) and moving in the direction \theta = {\pi \over 6}, the function is changing at a rate of approximately 1.37 units per unit length.
- (c) The slope of the tangent line to the curve C that is the intersection of the surface f(x, y) = {xe}^{y} + {ye}^{x}, and the plane perpendicular to the xy-plane that contains the line through point (0, 0, 0) in the direction \theta = {\pi \over 6}, is approximately 1.37.
f(x,y)=x\ln y at (5,1) in the direction \theta =\dfrac{ \pi }{4}
f(x,y)=\tan ^{-1}\dfrac{y}{x} at (1,1) in the direction of \mathbf{a}=3\mathbf{i}-4\mathbf{j}
- (a) {D}_{\bf u} {f}(1, 1) = -{{ 7} \over {10}} = - 0.7
- (b) Starting at the point (1, 1) and moving in the direction {\bf a} = 3{\bf i} - 4{\bf j}, the function is changing at a rate of -0.7 units per unit length.
- (c) The slope of the tangent line to the curve C that is the intersection of the surface f(x, y)=\tan ^{ - 1}{{y} \over {x}}, and the plane perpendicular to the xy-plane that contains the line through point (1, 1, 0) in the direction {\bf a} = 3{\bf i} - 4{\bf j}, is -0.7.
f(x,y)=\ln \sqrt{x^{2}+y^{2}} at (3,4) in the direction of \mathbf{a}=5\mathbf{i}+12\mathbf{j}
In Problems 17–32:
- (a) Find the gradient of f at the given point P.
- (b) Use the gradient to find the directional derivative of f at P in the direction from P to Q.
f(x,y)=xy^{2}+x^{2};\qquad P=(1,2), Q=(2,4)
- (a) {\bf\nabla} f(1,2)=6{\bf i}+4{\bf j}
- (b) {D}_{\bf u} {f}(1, 2) = {{14\sqrt 5 } \over 5}
f(x,y)=2xy+x^{2};\qquad P=(-1,1), Q=(1,2)
f(x,y)=2xy+x^{2};\qquad P=(0,3), Q=(4,1)
- (a) {\bf\nabla} f(0,3)=6{\bf i}
- (b) {D}_{\bf u} {f}(0, 3) = {{12\sqrt 5 } \over 5}
f(x,y)=3xy+y^{2};\qquad P=(2,1), Q=(4,1)
f(x,y)=xy+\sin x;\qquad P=(0,1), Q=(\pi ,2)
- (a) {\bf\nabla} f(0,1)=2{\bf i}
- (b) {D}_{\bf u} {f}(0, 1) = {{2\pi } \over {\sqrt {\pi ^2 + 1} }}
f(x,y)=e^{xy}+\sin y;\qquad P=\left( 0,\dfrac{\pi }{2}\right), Q=(1,0)
f(x,y)=\tan ^{-1}\dfrac{y}{x};\qquad P=(1,0), Q=(4,\pi )
- (a) {\bf\nabla} f(1,0)={\bf j}
- (b) {D}_{\bf u} {f}(1, 0) = {\pi \over {\sqrt {\pi ^2 + 9} }}
f(x,y)=\ln \sqrt{x^{2}+y^{2}};\qquad P=(3,4), Q=(0,5)
f(x,y)=x^{2}e^{y};\qquad P=(2,0), Q=(3,0)
- (a) {\bf\nabla} f(2,0)=4{\bf i}+4{\bf j}
- (b) {D}_{\bf u} {f}(2, 0) = 4
f(x,y)=e^{x^{2}+y^{2}};\qquad P=(1,2), Q=(2,3)
f(x,y,z)=x^{2}y-xyz^{2};\qquad P=(0,1,2), Q=(1,4,3)
- (a) {\bf\nabla} f(0,1,2)=-4{\bf i}
- (b) {D}_{\bf u} {f}(0, 1, 2) = -{{ 4\sqrt {11} } \over {11}}
f(x,y,z)=x^{2}y+y^{2}z+z^{2}x;\qquad P=(1,2,-1), Q=(2,0,1)
f(x,y,z)=z\tan ^{-1}\dfrac{y}{x};\qquad P= (1,1,3), Q= ( 2,0,-2)
- (a) {\bf\nabla} f(1,1,3)= -\dfrac{3}{2} {\bf i}+\dfrac{3}{2}{\bf j}+\dfrac{\pi}{4}{\bf k}
- (b) {D}_{\bf u} {f}(1, 1, 3) = -{{(12 + 5\pi )\sqrt 3 } \over {36}}
f(x,y,z)=\sin x\cos (y+z);\qquad P= (1,1,1), Q= (2,-1,0)
f(x,y,z)=\sqrt{x^{2}+y^{2}+z^{2}};\qquad P= (3,4,0), Q= ( 1,-1,1)
- (a) {\bf\nabla} f(3,4,0)=\dfrac{3}{5}{\bf i}+\dfrac{4}{5}{\bf j}
- (b) {D}_{\bf u} {f}(3, 4, 0) = -{{ 13\sqrt {30} } \over {75}}
f(x,y,z)=\dfrac{x}{\sqrt{x^{2}+2y^{2}+3z^{2}}};\qquad P= (1,2,1), Q= ( -1,1,1)
In Problems 33–40:
- (a) Find the direction for which the directional derivative of the function f is a maximum.
- (b) Find the maximum value of the directional derivative.
f(x.y) =xy^{2}+x^{2} at P=(-1,2)
- (a) {\bf u} = {{\sqrt 5 } \over {5}}{\bf i} - {2{\sqrt 5 } \over {5} }{\bf j}
- (b) \left\Vert\nabla f(-1,2) \right\Vert\;=\;2\sqrt{5}
f(x.y) =3xy+y^{2} at P=(2,1)
f(x.y) =xe^{y}+ye^{x} at P=(0,0)
- (a) {\bf u} = {{\sqrt 2 } \over 2}{\bf i} + {{\sqrt 2 } \over 2}{\bf j}
- (b) \left\Vert\nabla f(0,0) \right\Vert\; =\sqrt{2}
f(x.y) =x\ln y at P=(5,1)
f(x,y)=\dfrac{x}{x^{2}+y^{2}} at P=(1,2)
- (a) {\bf u}=\dfrac{3}{5}{\bf i}-\dfrac{4}{5}{\bf j}
- (b) \left\Vert\nabla f(1,2)\right\Vert\;=\dfrac{1}{5}
f(x,y)=\sqrt{x^{2}+y^{2}} at P=(3,4)
f( x.y,z) =z\tan ^{-1}\dfrac{y}{x} at P=(1,1,3)
- (a) {\bf u}=-\dfrac{6}{\sqrt{\pi^2+72}}{\bf i} + \dfrac{6}{\sqrt{\pi^2+72}}{\bf j} + \dfrac{\pi}{\sqrt{\pi^2+72}}{\bf k}
- (b) \left\Vert\nabla f(1,1,3)\right\Vert\;=\;\sqrt{\dfrac{9}{2}+\dfrac{\pi^2}{16}}
f( x.y,z) =\sqrt{x^{2}+y^{2}+z^{2}} at P=(3,4,0)
In Problems 41–46, graph the level curve of f containing the point P and the gradient {\bf\nabla\! }f at that point.
f(x,y)=x^{2}+y^{2} containing P=(3,4)

f(x,y)=x^{2}-y^{2} containing P=(2,-1)
f(x,y)=x^{2}-4y^{2} containing P=\left( 3,\dfrac{\sqrt{5}}{2}\right)
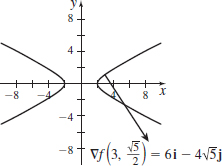
f(x,y)=x^{2}+4y^{2} containing P=(-2,0)
f(x,y)=x^{2}y containing P=\left( 3,\dfrac{1}{9}\right)
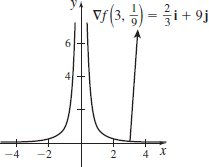
f(x,y)=xy containing P=(1,1)
Applications and Extensions
Heat Transfer A metal plate is placed on the xy-plane in such a way that the temperature T at any point (x,y) is given by T=e^{x}( \sin x+\sin y) {}^{\circ}{\rm C}.
- (a) What is the rate of change in temperature at (0,0) in the direction of 3\mathbf{i}-4\mathbf{j}?
- (b) At (0,0), in what direction is the temperature increasing most rapidly?
- (c) In what direction is the temperature decreasing most rapidly?
- (d) In what direction does the temperature remain the same?
- (a) The rate of change of temperature is -{{ 1} \over 5} ^{\circ}C per unit length in the direction 3i – 4j.
- (b) The temperature is increasing most rapidly in the direction \nabla T (0, 0) = {\bf i} + {\bf j} .
- (c) The temperature is decreasing most rapidly in the direction -\nabla T (0, 0) = -{\bf i} - {\bf j} .
- (d) The rate of change of temperature remains the same in the directions of -{\bf i} + {\bf j} and {\bf i}-{\bf j}.
873
Electrical Potential The electrical potential V at any point (x,y) is given by V=\ln \sqrt{x^{2}+y^{2}}. Find the rate of change of potential V at any point (x,y)\neq (0,0):
- (a) In a direction toward (0,0).
- (b) In the two directions orthogonal to a direction toward (0,0).
- (c) In what direction is the potential V increasing most rapidly?
- (d) In what direction is the potential V decreasing most rapidly?
Geography The surface of a hill is modeled by the equation z=( 8-2x^{2}-y^{2}) \rm{m}. See the figure below. If a freshwater spring is located at the point (1,2,2), in what direction will the water flow?

The graph of z and its level curves.
Water will flow in the direction -\nabla{\bf z}(1,2)=4{\bf i}+4{\bf j}.
Temperature Change Suppose that the temperature in degrees Celsius at each point of the coordinate plane is T=( 3x^{2}+4y^{2}+5) {}^{\circ}{\rm C}.
- (a) If we leave the point (3,4) heading for the point (4,3), eak how fast (in degrees per unit of distance) is the temperature changing at the point (4, 3)?
- (b) After reaching (4,3), in what direction should we go if we want to cool off as fast as possible? How fast is the temperature changing at the point (4,3)?
- (c) Suppose that we want to move away from (4,3) along a path of constant temperature. What is an equation of our path and what is the temperature?
- (d) A person at the origin may go in any direction and will experience the same rate of change of temperature. Why? What is the rate?
Temperature Change The temperature at any point (x,y) of a rectangular plate lying in the xy-plane is given by T=[ x\sin ( 2y) ] {}^{\circ}{\rm C}. Find the rate of change of temperature at the point \left( 1,\dfrac{\pi }{4}\right) in the direction making an angle of \dfrac{\pi }{6} with the positive x-axis.
The rate of change of temperature is {{\sqrt 3 } \over 2} ^{\circ}C per unit of distance in the u-direction.
Rate of Change Suppose that z=xy^{2}. In what direction(s) can we go from the point (-1,1) if we want the rate of change of z to be 2?
Rate of Change
- (a) Find the direction through the point (2,1) in which the function z=4x^{2}+9y^{2} has a maximum rate of change.
- (b) Verify that this direction is that of the normal to the curve 4x^{2}+9y^{2}=25 at the point (2,1). See the figure in next column.
- (c) Find the value of this maximum rate of change.
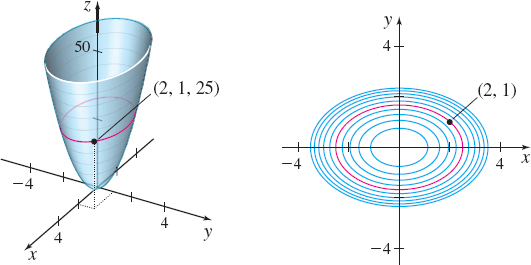
The graph of z and its level curves. The curve 4x^{2} +9y^{2} =25 appears in red.
- (a) The direction is {\bf u} = {8 \over {\sqrt {145} }}{\bf i} + {9 \over {\sqrt {145} }}{\bf j}.
- (b) See Student Solutions Manual.
- (c) The maximum rate of change is 2\sqrt {145}.
Show that the level curves of z = f(x,y) = x^{2}-y^{2} are orthogonal to the level curves of h(x,y)=xy for all (x_{0},y_{0})\neq (0,0). See the figure below.
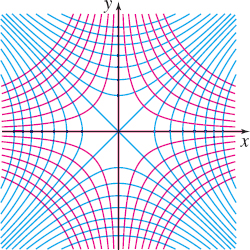
The level curves of z are in blue. The level curves of h are in red.
Find a unit vector \mathbf{u} that is normal to the level curve of f(x,y)=4x^{2}y through P=(1,-2) at P. See the figure below.
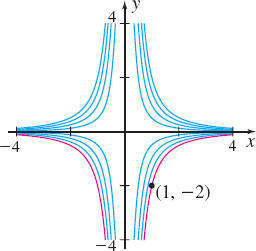
The level curves of f(x,y) = 4x^{2}y.
Vector  is normal to the level curve of f at P, as is
is normal to the level curve of f at P, as is 
Find a unit vector \mathbf{u} that is normal to the level curve of f(x,y)=2x^{2}+y^{2}+1 through P=(1,1) at P. See the figure below.
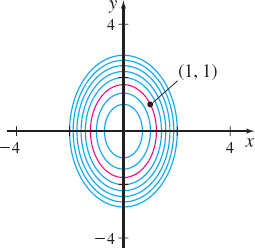
The level curves of f(x,y) = 2x^{2}+y^{2}+1.
874
Isothermal Curves Using the information from Example 5:
- (a) Find the level curves of T=T( x,y) =\dfrac{250}{\sqrt{ x^{2}+y^{2}}}.
- (b) Graph the level curves for T=25, 50, and 250.
- (c) Write the equation of the level curve for T that passes through the point ( -3,4).
- (d) Graph the level curve from (c) along with the vector {\bf\nabla} T( -3,4).
- (e) Since Example 5 deals with temperature, the level curves for T are called isothermal curves. Explain how they relate to the temperature T.
- (a) The level curves are circles of the form x^2 + y^2 = \left({{250} \over T}\right)^2.
- (b)

- (c) The level curve is x^{2}+y^{2} = 25.
- (d)
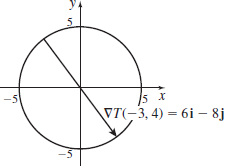
- (e) Answers will vary.
Mountaineering Suppose that you are climbing a mountain whose surface is modeled by the equation x^{2}+y^{2}-5x+z=0. (The x-axis points east, the y-axis north, and the z-axis up; units are in thousands of feet.)
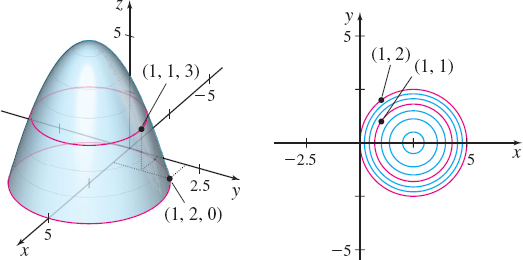
The graph of z and its level curves.
- (a) Your route is such that as you pass through the point (1,1,3), you are heading northeast. At what rate (with respect to distance) is your altitude changing at that point?
- (b) Another climber at (1,2,0) wants to reach the summit in as short a distance as possible. In what direction should he start? At what rate is his altitude changing when he starts?
- (c) A third climber at (2,1,5) wants to remain at the same altitude. In what direction(s) may she go?
Electrical Potential Suppose that the electrical potential (voltage V) at each point in space is V=e^{xyz} volts and that electric charges move in the direction of greatest potential drop (most rapid decrease of potential). In what direction does a charge at the point (1,-1,2) move? How fast does the potential change as the charge leaves this point?
The charge moves in the direction {\bf u} = {2 \over 3}{\bf i} - {2 \over 3}{\bf j} + {1 \over 3}{\bf k}. The electrical potential changes at a rate of -3e^{-2} volts per unit change in the u-direction.
Electric Field The electric field vector \mathbf{E} is the negative of the gradient of the electrostatic potential V. That is, \mathbf{E}=-{\bf\nabla}V. If Q is a point charge at the origin, then the electrostatic potential V at the point P(x,y,z) is given by V= \dfrac{kQ}{\sqrt{x^{2}+y^{2}+z^{2}}}, where k is a constant.
- (a) Find the electric field vector \mathbf{E} at the point P(x,y,z).
- (b) Use (a) to show that the magnitude of the electric field is \left\Vert \mathbf{E}\right\Vert = \dfrac{kQ}{r^{2}}, where r is the distance from the origin to the point P(x,y,z).
- (c) Verify that the electric field vector \mathbf{E} is normal to the equipotential surfaces (surfaces on which the electrostatic potential V is constant).
Modeling Temperature Change The temperature at each point of the region x^{2}+y^{2}+z^{2}\leq 9 is T=\sqrt{9-x^{2}-y^{2}-z^{2}} {}^{\circ}{\rm C}. If we start at the point (0,1,2) and move across the region in a straight path ending at (2,1,2), find the rate of change of T at an arbitrary point on the path.
-\dfrac{x}{\sqrt{4-x^2}}
Chemotaxis Chemotaxis is the phenomenon in which bodily cells, bacteria, and other organisms direct their movement according to a chemical stimulus. Suppose the concentration of a certain biochemical distribution at a wounded place is given by w=f(x,y,z)=\dfrac{1}{x^2 + y^2 +z^2}. If a cell that reacts by chemotaxis is located at the point (1,2,3), find the direction it will move by chemotaxis if the direction of movements is along the gradient of f.
Source: Problem submitted by the students at Minnesota State University
Gravitational Potential Energy In the study of mechanics in physics, it is shown that the gravitational force \mathbf{F}_{g} on an object equals the negative of the gradient of the gravitational potential energy U_{g} of the object. That is, \mathbf{F}_{g}=-{\bf\nabla } U_{g}. In a uniform gravitational field (such as near Earth’s surface), the gravitational potential energy is given by U_{g}=mgz, where m is the mass of an object, z (in meters) is its altitude above Earth’s surface, and g=9.8\; \rm{m}/\rm{s}^{2}. Use the gradient {\bf\nabla }U_{g} to show that the gravitational force is downward and has magnitude mg.
See Student Solutions Manual.
Gravitational Field Two objects of masses M and m are a distance r, in meters, apart. The gravitational potential energy between these objects is given by U_g=-G\dfrac{mM}{r}, where G=6.67\times 10^{-11}\;\rm{Nm}^{2}/\rm{kg}^{2}. If one object is at the origin and the other at the point (x,y,z), then the gravitational field \mathbf{F}_{g} equals -\bf\nabla U_g. Show that the magnitude of the force \mathbf{F}_{g} equals G\dfrac{mM}{r^2}.
Source: Problem contributed by the students at Minnesota State University
If the function z=f(x,y) is differentiable at a point P_{0}=(x_{0},y_{0}) and {\bf\nabla\! }f(x_{0},y_{0})\neq \mathbf{0}, show that D_{\mathbf{u}}f(x_{0},y_{0})=0 in the direction orthogonal to that of {\bf\nabla\! }f(x_{0},y_{0}).
See Student Solutions Manual.
Algebraic Properties of the Gradient If u=f(x,y) and v=g(x,y) are differentiable, show that:
- (a) {\bf\nabla }(ku)=k{\bf\nabla }u, where k is a constant.
- (b) {\bf\nabla }(u+v)={\bf\nabla }u+{\bf\nabla }v.
- (c) {\bf\nabla }(uv)=u{\bf\nabla }v+v{\bf\nabla }u.
- (d) {\bf\nabla }\left( \dfrac{u}{v}\right) =\dfrac{v{\bf\nabla }u-u{\bf\nabla }v}{v^{2}}.
- (e) {\bf\nabla }u^{a }=a u^{a -1}{\bf\nabla }u, where a a real number.
Show that for a nonzero vector \mathbf{a}=a_{1}\mathbf{i} +a_{2}\mathbf{j} and a differentiable function z=f(x,y), D_{\mathbf{u}}f(x,y)=\frac{a_{1}\dfrac{\partial f}{\partial x}+a_{2}\dfrac{ \partial f}{\partial y}}{\sqrt{a_{1}^{2}+a_{2}^{2}}}
where \mathbf{u}=\dfrac{\mathbf{a}}{\Vert \mathbf{a}\Vert }.
See Student Solutions Manual.
875
Let F(x,y)=0 be the equation of a curve in the xy-plane. If F is differentiable and if (x_{0},y_{0}) is a point on the curve, show eak that {\bf\nabla\! }F(x_{0},y_{0}) is normal to the curve at (x_{0},y_{0}).
Use Problem 68 to show that the tangent line to the curve F(x,y)=0 at (x_{0},y_{0}) is given by a(x-x_{0})+b(y-y_{0})=0, where a=F_{x}(x_{0},y_{0}) and b=F_{y}(x_{0},y_{0}). (Assume that a and b are not both 0.)
See Student Solutions Manual.
Use Problem 69 to find the following tangent lines to the hyperbola x^{2}-y^{2}=16:
- (a) The tangent line at (5,3). Check the result by finding \dfrac{dy}{dx} at (5,3) using implicit differentiation.
- (b) The tangent line at (4,0). Note that this tangent line is vertical and requires special treatment in single variable calculus.
Suppose z=f(x,y) has directional derivatives in all directions. Must f be differentiable? Explain.
Function f is not necessarily differentiable. See Student Solutions Manual.
If f(x,y,z)=z^{3}+3xz-y^{2}, find the directional derivative of f at (1,2,1) in the direction of the line x-1=y-2=z-1.
Challenge Problems
Let \mathbf{r}=x\mathbf{i}+y\mathbf{j} and r=\left\Vert \mathbf{r}\right\Vert =\sqrt{x^{2}+y^{2}}.
- (a) Show that {\bf\nabla }r^{n}=nr^{n-2}\mathbf{r}.
- (b) Show that {\bf\nabla }g(r)=g′ (r)\dfrac{\mathbf{r}}{r}.
- (c) Show that D_{\mathbf{u}}[g(r)]=\dfrac{g^{\prime }(r)}{r}(\mathbf{u}\,{\bf\cdot}\, \mathbf{r}).
- (d) Show that {\bf\nabla }\left( \dfrac{x}{r}\right) =\dfrac{\mathbf{i}}{r}-\left( \dfrac{x}{r}\right) \left( \dfrac{\mathbf{r}}{r^{2}}\right).
See Student Solutions Manual.
Find the directional derivative of f(x,y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{\sin (x^{2}+y^{2})}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0) \\ 1 & \hbox{if} & (x,y)=(0,0) \end{array} \right.
at (0,0) in the direction of \mathbf{a}=\mathbf{i}+\mathbf{j}.
Show that if {\bf\nabla\! }f(x,y)=c(x\mathbf{i}+y\mathbf{j}) , where c is a constant, then f(x,y) is constant on any circle of radius k, centered at (0,0).
See Student Solutions Manual.
The Gradient Is Normal to the Level Surface Show that if the function w=f(x,y,z) is differentiable at a point P_{0}=(x_{0},y_{0},z_{0}), and if {\bf\nabla\! }f(x_{0},y_{0},z_{0}) \neq \mathbf{0}, then the gradient {\bf\nabla\! }f(x_{0},y_{0},z_{0}) is normal to the level surface of f through P_{0}.
Let z=f(x,y) have continuous second-order partial derivatives. If \mathbf{u}=u_{1}\mathbf{i}+u_{2}\mathbf{j} is a unit vector, we have a directional derivative D_{\mathbf{u}}f(x,y)=g(x,y). If g(x,y) is differentiable and \mathbf{v}=v_{1}\mathbf{i}+v_{2}\mathbf{j} is a unit vector, we have a directional derivative D_{\mathbf{v}}g(x,y). We can view this second quantity as a second-order directional derivative for z=f(x,y). Express it in terms of f_{xx}, f_{xy}, and f_{yy} by showing that it has the value u_{1}v_{1}f_{xx}+(u_{1}v_{2}+u_{2}v_{1})f_{xy}+u_{2}v_{2}f_{yy}
See Student Solutions Manual.
Assuming that b\neq 0 in Problem 69, show that the slope of the tangent line to the curve F(x,y)=0 at (x_{0},y_{0}) is m=-\dfrac{ F_{x}(x_{0},y_{0})}{F_{y}(x_{0},y_{0})}. (This is a proof of the Implicit Differentiation Formula I from Chapter 12, Section 12.5.)
