OBJECTIVES

When you finish this section, you should be able to:

1. Differentiate functions of two or more variables where each variable is a function of a single variable (p. 849)
2. Differentiate functions of two or more variables where each variable is a function of two or more variables (p. 851)
3. Differentiate an implicitly-defined function of two or more variables (p. 853)
4. Use a Chain Rule in a proof (p. 855)

NEED TO REVIEW?

The Chain Rule is discussed in Section 3.1, pp. 198-205.

THEOREM Chain Rule I: One Independent Variable

If \(x=x(t)\) and \(y=y(t)\) are differentiable functions of \(t\), and if \( z=f(x,y)\) is a differentiable function of \(x\) and \(y\), then \(z=f(x(t),y(t))\) is a differentiable function of \(t\). Moreover, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{{ \dfrac{dz}{dt}=\dfrac{\partial z}{\partial x}\dfrac{dx}{dt}+\dfrac{\partial z}{\partial y}\dfrac{dy}{dt} }}}\]

Proof

Since \(\dfrac{dz}{dt}=\lim\limits_{\Delta t\rightarrow 0} \dfrac{\Delta z}{\Delta t}\), we seek an expression for \(\Delta z\). Since \( z=f(x,y)\) is differentiable, the change \(\Delta z\) is \begin{equation*} \Delta z=\frac{\partial z}{\partial x}\Delta x+\frac{\partial z}{\partial y} \Delta y+\eta _{1}\Delta x+\eta _{2}\Delta y \end{equation*}

where \(\eta _{1}\) and \(\eta _{2}\) are functions of \(\Delta x\) and \(\Delta y\) and \(\lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{1}=0\) and \( \lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)} \eta _{2}=0\). Next we divide both sides by \(\Delta t.\) \begin{equation*} \dfrac{\Delta z}{\Delta t}=\frac{\partial z}{\partial x}\dfrac{\Delta x}{ \Delta t}+\frac{\partial z}{\partial y}\dfrac{\Delta y}{\Delta t}+\eta _{1} \dfrac{\Delta x}{\Delta t}+\eta _{2}\dfrac{\Delta y}{\Delta t} \end{equation*}

Then \[ \frac{dz}{dt}=\lim_{\Delta t\rightarrow 0}\frac{\Delta z}{\Delta t} =\lim_{\Delta t\rightarrow 0}\;\left[ \frac{\partial z}{\partial x}\frac{ \Delta x}{\Delta t}+\frac{\partial z}{\partial y}\frac{\Delta y}{\Delta t} +\eta _{1}\frac{\Delta x}{\Delta t}+\eta _{2}\frac{\Delta y}{\Delta t}\right] \]

In the right-hand expression, \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{ \partial z}{\partial y}\) are evaluated at \((x(t),y(t))\) and do not depend on \(\Delta t\). Also, since \(x=x( t)\) and \(y=y( t)\) are differentiable, \begin{equation*} \lim\limits_{\Delta t\rightarrow 0}\dfrac{\Delta x}{\Delta t}=\frac{dx}{dt} \qquad \hbox{and}\qquad \lim_{\Delta t\rightarrow 0}\dfrac{\Delta y}{\Delta t }=\dfrac{dy}{dt} \end{equation*}

Furthermore, as \(\Delta t\rightarrow 0\), then \((\Delta x,\Delta y)\rightarrow (0,0)\), so that \(\eta _{1}\rightarrow 0\) and \(\eta _{2}\rightarrow 0\). Putting this all together, we get \begin{eqnarray*} \frac{dz}{dt}& =&\frac{\partial z}{\partial x}\lim_{\Delta t\rightarrow 0} \frac{\Delta x}{\Delta t}+\frac{\partial z}{\partial y}\lim_{\Delta t\rightarrow 0}\frac{\Delta y}{\Delta t}+\lim_{\Delta t\rightarrow 0}\eta _{1}\cdot \lim_{\Delta t\rightarrow 0}\frac{\Delta x}{\Delta t}+\lim_{\Delta t\rightarrow 0}\eta _{2}\cdot \lim_{\Delta t\rightarrow 0}\frac{\Delta y}{ \Delta t} \nonumber \\[4pt] & =&\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y} \frac{dy}{dt}+0\cdot \frac{dx}{dt}+0\cdot \frac{dy}{dt}=\frac{\partial z}{ \partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} \end{eqnarray*}

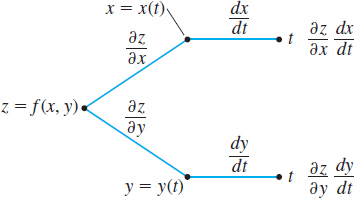
Differentiating a Function of Two Variables Where Each Variable Is a Function of \(t\)

Let \(z=x^{2}y-y^{2}x,\) where \(x=\sin t\) and \(y=e^{t}\). Find \(\dfrac{dz}{dt}\).

Solution We begin by finding the partial derivatives of \(z\), \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{\partial z}{\partial y}\), and the derivatives \(\dfrac{dx}{dt}\) and \(\dfrac{dy}{dt}.\) \[ \dfrac{\partial z}{\partial x}=2xy-y^{2}\qquad \dfrac{ \partial z}{\partial y}=x^{2}-2xy\qquad \dfrac{dx}{dt} =\cos t\qquad \dfrac{dy}{dt}=e^{t} \]

Then we use Chain Rule I to find \(\dfrac{dz}{dt}.\) \[ \begin{eqnarray*} \frac{dz}{dt}\underset{ \underset{ \color{#0066A7}{\hbox{Chain Rule I}}} {\color{#0066A7}{\uparrow }}} {=}\frac{ \partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{ dt}=(2xy-y^{2})(\cos t)+(x^{2}-2xy)(e^{t}) \tag{1} \end{eqnarray*} \]

Since \(z\) is a function of \(t,\) we express \(\dfrac{dz}{dt}\) in terms of \(t.\) \[ \begin{eqnarray*} \frac{dz}{dt}&&=(2e^{t}\sin t-e^{2t})(\cos t)+(\sin ^{2}t-2e^{t}\sin t)(e^{t})\qquad {\color{#0066A7}{\hbox{\(x=\sin t, y=e^{t}\)}}} \nonumber\\ &&=e^{t}[ \sin ( 2t) -e^{t}\cos t+\sin ^{2}t-2e^{t}\sin t] \qquad {\color{#0066A7}{\hbox{\(2\sin t\cos t =\sin (2t) \)}}} \tag{2} \end{eqnarray*} \]

NOW WORK

Problem 3.

Differentiating a Function of Two Variables Where Each Variable Is a Function of \(t\)

Let \(z=e^{x}\sin y,\) where \(x=e^{t}\) and \(y=\dfrac{\pi }{3}e^{-t}\). Find \( \dfrac{dz}{dt}\) when \(t=0\).

Solution We begin by finding the partial derivatives of \(z\), \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{\partial z}{\partial y}\), and the derivatives \(\dfrac{dx}{dt}\) and \(\dfrac{dy}{dt}\). \[ \dfrac{\partial z}{\partial x}=e^{x}\sin y\qquad \dfrac{\partial z}{\partial y}=e^{x}\cos y\qquad \dfrac{dx}{dt}=e^{t}\qquad \dfrac{dy}{dt}=-\dfrac{\pi }{3}e^{-t} \]

Then we use Chain Rule I to find \(\dfrac{dz}{dt}\). \[ \begin{eqnarray*} \frac{dz}{dt}\underset{ \underset{ \color{#0066A7}{\hbox{Chain Rule I}}} {\color{#0066A7}{\uparrow }}} {=}\frac{ \partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{ dt}=(e^{x}\sin y)e^{t}+(e^{x}\cos y)\left( -\frac{\pi }{3}e^{-t}\right)\\[-9pt] \end{eqnarray*} \]

We can stop here and evaluate \(\dfrac{dz}{dt}.\) When \(t=0\), then \(x=e^{0}=1\) and \(y=\dfrac{\pi }{3}e^{0}=\dfrac{\pi }{3}\). So, when \(t=0\), \[ \frac{dz}{dt}=\left( e\sin \frac{\pi }{3}\right) (1)+\left( e\cos \frac{\pi }{3}\right) \left( -\frac{\pi }{3}\right) =\frac{e\sqrt{3}}{2}-\frac{\pi e}{6 }=\frac{e}{6}(3\sqrt{3}-\pi ) \]

NOW WORK

Problem 9.

Differentiating a Function of Three Variables Where Each Variable Is a Function of \(t\)

If \(w=x^{2}y+y^{2}z,\) where \(x=t\), \(y=t^{2}\), and \(z=t^{3}\), then \(w\) is a function of \(t,\) and \begin{eqnarray*} \dfrac{dw}{dt}& =&\dfrac{\partial w}{\partial x}\dfrac{dx}{dt}+\dfrac{\partial w}{ \partial y}\dfrac{dy}{dt}+\dfrac{\partial w}{\partial z}\dfrac{dz}{dt}=\, \underset{\color{#0066A7}{\dfrac{\partial w}{\partial x}}}{\underbrace{(2xy)}}\underset{\color{#0066A7}{\dfrac{ dx}{dt}}}{\underbrace{(1)}}+\underset{\color{#0066A7}{\dfrac{\partial w}{\partial y}}}{ \underbrace{(x^{2}+2yz)}}\underset{\color{#0066A7}{\dfrac{dy}{dt}}}{\underbrace{(2t)}}+ \underset{\color{#0066A7}{\dfrac{\partial w}{\partial z}}}{\underbrace{(y^{2})}}\underset{\color{#0066A7}{ \dfrac{dz}{dt}}}{\underbrace{(3t^{2})}} \nonumber \\ &=& 2t^{3}+(t^{2}+2t^{5})(2t)+(t^{4})(3t^{2})=7t^{6}+4t^{3} \nonumber \end{eqnarray*}

NOW WORK

Problem 17.

THEOREM Chain Rule II: Two Independent Variables

Let \(z=f( g(u,v),h(u,v))\) be the composite of \(z=f(x,y),\) where \(x=g(u,v)\) and \(y=h(u,v)\). If \(g\) and \(h\) are each continuous and have continuous first-order partial derivatives at a point \((u,v)\) in the interior of the domains of both \(g\) and \(h\), and if \(f\) is differentiable in some disk centered at the point \((x,y)=( g(u,v),h(u,v))\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{{ \dfrac{\partial z}{\partial u}=\dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial u}+\dfrac{\partial z}{\partial y} \dfrac{\partial y}{\partial u} \qquad \hbox{and} \qquad \dfrac{\partial z}{ \partial v}=\dfrac{\partial z}{\partial x}\dfrac{\partial x}{\partial v}+ \dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial v} }}} \]

Proof

To find \(\dfrac{\partial z}{\partial u}\), we hold \(v\) fixed. Then \(x=g(u,v)\) and \(y=h(u,v)\) are functions of \(u\) alone, and we can use Chain Rule I. Then \(\dfrac{\partial z}{\partial u}=\dfrac{\partial z}{ \partial x}\dfrac{dx}{du}+\dfrac{\partial z}{\partial y}\dfrac{dy}{du}.\) Now replace \(\dfrac{dx}{du}\) with \(\dfrac{\partial x}{\partial u}\), and replace \( \dfrac{dy}{du}\) with \(\dfrac{\partial y}{\partial u}\).

A similar argument is used for finding \(\dfrac{\partial z}{\partial v}\).

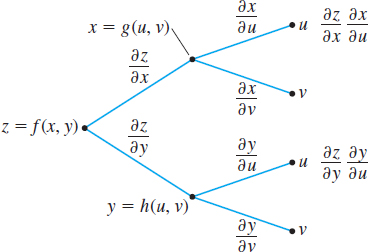
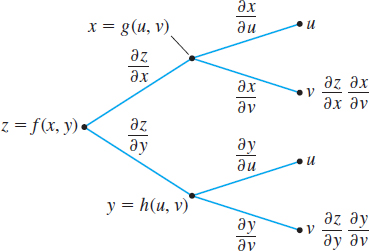
Differentiating a Function of Two Variables Where Each Variable Is a Function of Two Variables

Find \(\dfrac{\partial z}{\partial u}\) and \(\dfrac{\partial z}{\partial v}\) if \(z=f(x,y) =x^{2}+xy-y^{2}\) and \(x=e^{2u+v}\) and \(y=\ln \dfrac{ v}{u}.\)

Solution The function \(z=f(x,y)\) is a composite function of two independent variables \(u\) and \(v.\) So, we use Chain Rule II. \[ \dfrac{\partial z}{\partial u}=\frac{\partial z}{\partial x}\frac{\partial x}{ \partial u}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial u} \]

Since \[ \dfrac{\partial z}{\partial x}=2x+y\qquad \dfrac{ \partial z}{\partial y}=x-2y\qquad \dfrac{\partial x }{\partial u}=2e^{2u+v}\qquad \dfrac{\partial y}{\partial u} =\dfrac{\partial }{\partial u}( \ln v-\ln u) =-\dfrac{1}{u} \]

we have \begin{eqnarray*} \frac{\partial z}{\partial u}&=&\underset{\color{#0066A7}{\dfrac{\partial z}{\partial x}}}{ \underbrace{(2x+y)}}\underset{\color{#0066A7}{\dfrac{\partial x}{\partial u}}}{\underbrace{ (2e^{2u+v})}}+\underset{\color{#0066A7}{\dfrac{\partial z}{\partial y}}}{\underbrace{(x-2y)}}\underset{\color{#0066A7}{\dfrac{\partial y}{\partial u}}} {\underbrace{\left( -\dfrac{1}{u}\right) }}\\[4pt] &=&\left(2e^{2u+v}+\ln \dfrac{v}{u}\right) ( 2e^{2u+v}) -\left(e^{2u+v}-2\ln \dfrac{v}{u}\right) \left( \dfrac{1}{u}\right) \qquad \color{#0066A7}{{\hbox{\(x=e^{2u+v}; y=\ln \dfrac{v}{u}\)}}} \end{eqnarray*}

Similarly, since \(\dfrac{\partial x}{\partial v}=e^{2u+v}\) and \(\dfrac{ \partial y}{\partial v}=\dfrac{1}{v},\) we have \begin{eqnarray*} \dfrac{\partial z}{\partial v}&=&\underset{\color{#0066A7}{\dfrac{\partial z}{\partial x}}}{ \underbrace{(2x+y)}}\underset{\color{#0066A7}{\dfrac{\partial x}{\partial v}}}{\underbrace{ (e^{2u+v})}}+\underset{\color{#0066A7}{\dfrac{\partial z}{\partial y}}}{\underbrace{(x-2y)}} \underset{\color{#0066A7}{\dfrac{\partial y}{\partial v}}}{\underbrace{\left( \dfrac{1}{v} \right) }}\\[4pt] &=&\left( 2e^{2u+v}+\ln \dfrac{v}{u}\right) ( e^{2u+v}) +\left( e^{2u+v}-2~\ln \dfrac{v}{u}\right) \left( \dfrac{1}{v}\right) \qquad \color{#0066A7}{{\hbox{\(x=e^{2u+v}; y=\ln \dfrac{v}{u}\)}}}\qquad \end{eqnarray*}

NOW WORK

Problem 31.

Differentiating a Function of Three Variables Where Each Variable Is a Function of Four Variables

Find \(\dfrac{\partial f}{\partial u},\) \(\dfrac{\partial f}{\partial v},\) \(\dfrac{\partial f}{\partial w},\) \(\dfrac{\partial f}{\partial t}\) for the function \(f(x,y,z)=x^{2}+y^{2}+z^{2},\) where \(x=uvwt\), \(y=e^{u+v+w+t}\), and \(z=u+2v+3w+4t\).

Solution We use an extension of Chain Rule II. \[ \begin{array}{lllllll} \dfrac{\partial f}{\partial u} &=&\dfrac{\partial f}{\partial x}\dfrac{\partial x}{\partial u}+\dfrac{\partial f}{\partial y}\dfrac{\partial y}{\partial u}+ \dfrac{\partial f}{\partial z}\dfrac{\partial z}{\partial u} & \dfrac{ \partial f}{\partial v}&=&\dfrac{\partial f}{\partial x}\dfrac{\partial x}{ \partial v}+\dfrac{\partial f}{\partial y}\dfrac{\partial y}{\partial v}+\dfrac{ \partial f}{\partial z}\dfrac{\partial z}{\partial v} \nonumber\\ &=&(2x)(vwt)+(2y)(e^{u+v+w+t})+(2z)(1) & &=&(2x)(uwt)+(2y)(e^{u+v+w+t})+(2z)(2) \nonumber \\ &=&2uv^{2}w^{2}t^{2}+2e^{2(u+v+w+t)}+2(u+2v+3w+4t) & &=&2u^{2}vw^{2}t^{2}+2e^{2(u+v+w+t)}+4(u+2v+3w+4t) \nonumber \\[1pc] \dfrac{\partial f}{\partial w} &=&\dfrac{\partial f}{\partial x}\dfrac{\partial x}{\partial w}+\dfrac{\partial f}{\partial y}\dfrac{\partial y}{\partial w}+ \dfrac{\partial f}{\partial z}\dfrac{\partial z}{\partial w} & \dfrac{\partial f}{ \partial t}&=&\dfrac{\partial f}{\partial x}\dfrac{\partial x}{\partial t}+\dfrac{ \partial f}{\partial y}\dfrac{\partial y}{\partial t}+\dfrac{\partial f}{ \partial z}\dfrac{\partial z}{\partial t} \nonumber \\ &=&(2x)(uvt)+(2y)(e^{u+v+w+t})+(2z)(3) & &=&(2x)(uvw)+(2y)(e^{u+v+w+t})+(2z)(4) \nonumber \\ &=&2u^{2}v^{2}wt^{2}+2e^{2(u+v+w+t)}+6(u+2v+3w+4t) & &=&2u^{2}v^{2}w^{2}t+2e^{2(u+v+w+t)}+8(u+2v+3w+4t) \end{array} \]

Again, notice that the partial derivatives of \(f\) in Example 5 are expressed in terms of \(u, v, w\), and \(t\) alone.

NOW WORK

Problem 37.

NEED TO REVIEW?

Implicit differentiation is discussed in Section 3.2, pp. 209-213.

Implicit Differentiation Formula I

Suppose \(F\) is a differentiable function and \(y=f(x)\) is a function defined implicitly by the equation \(F(x,y)=0\). Then \[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{{ \dfrac{dy}{dx}=-\dfrac{F_{x}(x,y)}{F_{y}(x,y)} }}} \tag{3} \end{equation*}\]

provided \(\dfrac{\partial F}{\partial y}=F_{y}(x,y)\neq 0.\)

Differentiating an Implicitly Defined Function

Find \(\dfrac{dy}{dx}\) if \(y=f(x)\) is defined implicitly by \( F(x,y)=e^{y}\cos x-x-1=0\).

Solution First we find the partial derivatives of \(F\). \[ F_{x}=\dfrac{\partial F}{\partial x}=-e^{y}\sin x-1\qquad \hbox{and} \qquad F_{y}=\dfrac{ \partial F}{\partial y}=e^{y}\cos x \]

Then we use (3). If \(e^{y}\cos x\neq 0\), \[ \frac{dy}{dx}=-\frac{F_{x}}{F_{y}}=-\frac{-e^{y}\sin x-1}{e^{y}\cos x}=\frac{e^{y}\sin x+1}{e^{y}\cos x} \]

NOW WORK

Problem 41.

Implicit Differentiation Formulas II

If a differentiable function \(z=f(x,y)\) is defined implicitly by the equation \(F(x,y,z)=0\), then \[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{{ \dfrac{\partial z}{\partial x}=-\dfrac{F_{x}(x,y,z)}{ F_{z}(x,y,z)}\qquad \hbox{and} \qquad \dfrac{\partial z}{\partial y}=-\dfrac{F_{y}(x,y,z)}{ F_{z}(x,y,z)} }}} \tag{4} \end{equation*} \]

provided \(\dfrac{\partial F}{\partial z}=F_{z}(x,y,z)\neq 0.\)

Differentiating an Implicitly Defined Function

Find \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{\partial z}{\partial y}\) if \(z=f(x,y) \) is defined implicitly by the function \[ F(x,y,z)=x^{2}z^{2}+y^{2}-z^{2}+6yz-10=0. \]

Solution First we find the partial derivatives of \(F.\) \begin{equation*} F_{x}=\dfrac{\partial F}{\partial x}=2xz^{2}\qquad F_{y}=\dfrac{ \partial F}{\partial y}=2y+6z\qquad F_{z}=\dfrac{\partial F}{\partial z} =2x^{2}z-2z+6y \end{equation*}

Then we use (4). If \(F_{z}=2x^{2}z-2z+6y\neq 0\), \[ \dfrac{\partial z}{\partial x}=-\dfrac{2xz^{2}}{2x^{2}z-2z+6y}=-\dfrac{ xz^{2}}{x^{2}z-z+3y} \]

and \[ \dfrac{\partial z}{\partial y}=-\dfrac{2y+6z}{ 2x^{2}z-2z+6y}=-\dfrac{y+3z}{x^{2}z-z+3y} \]

NOW WORK

Problem 49.

Using a Chain Rule in a Proof

Let \(p=f(v-w, v-u, u-w)\) be a differentiable function. Show that \[ \frac{\partial p}{\partial u}+\frac{\partial p}{\partial v}+\frac{\partial p}{\partial w}=0 \]

Solution Let \(x=v-w\), \(y=v-u\), and \(z=u-w\). Then \(p=f(x,y,z)\). We use an extension of Chain Rule II. Since \(\dfrac{\partial x}{\partial u}=0,\) \(\dfrac{\partial y}{\partial u} =-1,\) and \(\dfrac{\partial z}{\partial u}=1,\) we have \[ \frac{\partial p}{\partial u}=\frac{\partial p}{\partial x}\frac{\partial x}{ \partial u}+\frac{\partial p}{\partial y}\frac{\partial y}{\partial u}+\frac{ \partial p}{\partial z}\frac{\partial z}{\partial u}=\frac{\partial p}{ \partial x}(0)+\frac{\partial p}{\partial y}(-1)+\frac{\partial p}{\partial z }(1)=-\frac{\partial p}{\partial y}+\frac{\partial p}{\partial z}\hbox{ } \]

Since \(\dfrac{\partial x}{\partial v}=1,\) \(\dfrac{\partial y}{\partial v}=1,\) and \(\dfrac{\partial z}{\partial v}=0,\) we have \[ \frac{\partial p}{\partial v}=\frac{\partial p}{\partial x}\frac{\partial x}{ \partial v}+\frac{\partial p}{\partial y}\frac{\partial y}{\partial v}+\frac{ \partial p}{\partial z}\frac{\partial z}{\partial v}=\frac{\partial p}{ \partial x}(1)+\frac{\partial p}{\partial y}(1)+\frac{\partial p}{\partial z} (0)=\frac{\partial p}{\partial x}+\frac{\partial p}{\partial y} \]

Since \(\dfrac{\partial x}{\partial w}=-1,\) \(\dfrac{\partial y}{\partial w} =0,\) and \(\dfrac{\partial z}{\partial w}=-1,\) we have \[ \frac{\partial p}{\partial w}=\frac{\partial p}{\partial x}\frac{\partial x}{ \partial w}+\frac{\partial p}{\partial y}\frac{\partial y}{\partial w}+\frac{ \partial p}{\partial z}\frac{\partial z}{\partial w}=\frac{\partial p}{ \partial x}(-1)+\frac{\partial p}{\partial y}(0)+\frac{\partial p}{\partial z }(-1)=-\frac{\partial p}{\partial x}-\frac{\partial p}{\partial z} \]

Adding these, we get \[ \underset{\color{#0066A7}{\hbox{ }\hspace{5pc}\dfrac{{\partial p}}{{\partial u}}}}{\dfrac{ \partial p}{\partial u}+\dfrac{\partial p}{\partial v}+\dfrac{\partial p}{ \partial w}=\underbrace{\left( -\frac{\partial p}{\partial y}+\frac{\partial p}{\partial z}\right) }}+\underset{\color{#0066A7}{\dfrac{{\partial p}}{{ \partial v}}}}{\underbrace{\left( \frac{\partial p}{\partial x}+\frac{ \partial p}{\partial y}\right) }}+\underset{\color{#0066A7}{\dfrac{{\partial p}}{ {\partial w}}}}{\underbrace{\left( -\frac{\partial p}{\partial x}- \frac{\partial p}{\partial z}\right) \,\,\,}}=0 \]

NOW WORK

Problem 65.