3.2 Implicit Differentiation; Derivatives of the Inverse Trigonometric FunctionsPrinted Page 209
209
OBJECTIVES
When you finish this section, you should be able to:
So far we have differentiated only functions y=f(x) where the dependent variable y is expressed explicitly in terms of the independent variable x. There are functions that are not written in the form y=f(x), but are written in the implicit form F(x,y)=0. For example, x and y are related implicitly in the equations xy−4=0y2+3x2−1=0ex2−y2−cos (xy)=0
NEED TO REVIEW?
The implicit form of a function is discussed in Section P.1, p. 4.
The implicit form xy−4=0 can easily be written explicitly as the function y=4x. Also, y2+3x2−1=0 can be written explicitly as the two functions y1=√1−3x2 and y2=−√1−3x2. In the equation ex2−y2−cos (xy)=0, it is impossible to express y as an explicit function of x. In this case, and in many others, we use the technique of implicit differentiation to find the derivative.
1 Find a Derivative Using Implicit DifferentiationPrinted Page 209
The method used to differentiate an implicitly defined function is called implicit differentiation. It does not require rewriting the function explicitly, but it does require that the dependent variable y is a differentiable function of the independent variable x. So throughout the section, we make the assumption that there is a differentiable function y=f(x) defined by the implicit equation. This assumption made, the method consists of differentiating both sides of the implicitly defined function with respect to x and then solving the resulting equation for dydx.
210
EXAMPLE 1Finding a Derivative Using Implicit Differentiation
Find dydx if xy−4=0.
- (a) Use implicit differentiation.
- (b) Solve for y and then differentiate.
- (c) Verify the results of (a) and (b) are the same.
Solution (a) To differentiate implicitly, we assume y is a differentiable function of x and differentiate both sides with respect to x. ddx(xy−4)=ddx0Differentiate both sides with respect to x.ddx(xy)−ddx4=0Use the Difference Rule.x⋅ddxy+(ddxx)y−0=0Use the Product Rule.xdydx+y=0Simplify.dydx=−yxSolve fordydx.(1)
(b) Solve xy−4=0 for y, obtaining y=4x=4x−1. Then dydx=ddx(4x−1)=−4x−2=−4x2
(c) At first glance, the results in (1) and (2) appear to be different. However, since xy−4=0, or equivalently, y=4x, the result from (1) becomes dydx=↑(1)−yx=↑y=4x−4xx=−4x2 which is the same as (2).
In most instances, we will not know the explicit form of the function (as we did in Example 1) and so we will leave the derivative dydx expressed in terms of x and y [as in (1)].
NOW WORK
The Power Rule for Functions is ddx[f(x)]n=n[f(x)]n−1f′(x) where n is an integer. If y=f(x), it takes the form \bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{d}{dx}y^{n}=ny^{n-1}\dfrac{dy}{dx}}
This is convenient notation to use with implicit differentiation when y^n appears. \dfrac{d}{dx}y\underset{\underset{\color{#0066A7}{\hbox{\(n\)=1}}}{\color{#0066A7}{\uparrow}}}{=}1\cdot \dfrac{dy}{dx}=\dfrac{dy}{dx}\quad\quad \dfrac{d}{dx}y^{2}\underset{\underset{\color{#0066A7}{\hbox{\(n\)=2}}}{\color{#0066A7}{\uparrow}}}{=}2y\dfrac{dy}{dx}\quad\quad \dfrac{d}{dx}y^{3}\underset{\underset{\color{#0066A7}{\hbox{\(n=3\)}}}{\color{#0066A7}{\uparrow}}}{=}3y^{2}\dfrac{dy}{dx}
211
To differentiate an implicit function:
- Assume that y is a differentiable function of x.
- Differentiate both sides of the equation with respect to x.
- Solve the resulting equation for y^\prime =\dfrac{dy}{dx}.
EXAMPLE 2Finding a Derivative Using Implicit Differentiation
Find \dfrac{dy}{dx} if 3x^{2}+4y^{2}=2x.
Solution We assume that y is a differentiable function of x and differentiate both sides with respect to x. \begin{eqnarray*} \begin{array}{rl@{\qquad}l} \dfrac{d}{dx} ( 3x^{2}+4y^{2}) &= \dfrac{d}{dx}(2x) & {\color{#0066A7}{\hbox{Differentiate both sides with respect to}\; x.}}\\ \dfrac{d}{dx} (3x^{2}) +\dfrac{d}{dx}( 4y^{2}) &= 2 & {\color{#0066A7}{\hbox{Sum Rule}.}} \\ 3\dfrac{d}{dx}x^{2}+4\dfrac{d}{dx}y^{2} &=2 &{\color{#0066A7}{\hbox{Constant Multiple Rule}.}}\\ 6x+4\!\left( 2y\dfrac{dy}{dx}\right) &= 2 &{\color{#0066A7}{\dfrac{d}{dx}{y}^{{ 2}}{=2y} \dfrac{dy}{dx}}}\\ 6x+8y\dfrac{dy}{dx} &= {2} & {\color{#0066A7}{\hbox{Simplify.}}}\\ \dfrac{dy}{dx} &= \dfrac{2-6x}{8y}=\dfrac{1-3x}{4y} & {\color{#0066A7}{\hbox{Solve for}\; \dfrac{dy}{dx}.}} \end{array} \end{eqnarray*} provided y\ne 0.
Notice in Example 2 that \dfrac{dy}{dx} is expressed in terms of x and y.
NOW WORK
EXAMPLE 3Using Implicit Differentiation to Find an Equation of a Tangent Line
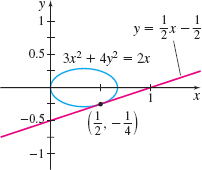
Find an equation of the tangent line to the graph of the ellipse 3x^{2}+4y^{2}=2x at the point \left( \dfrac{1}{2},-\dfrac{1}{4}\right).
Solution First we find the slope of the tangent line. We use the result from Example 2, and evaluate \dfrac{dy}{dx}=\dfrac{1-3x}{4y} at \left( \dfrac{1}{2},-\dfrac{1}{4}\right) . \begin{eqnarray*} && \dfrac{dy}{dx}=\dfrac{1-3x}{4y} \underset{\underset{\color{#0066A7}{x=\tfrac{1}{2},y=-\dfrac{1}{4}}}{\color{#0066A7}{{\left\uparrow{\vphantom{\vrule width0pc height12.5pt depth0pt}}\right.}}}}{=} \dfrac{1-3\cdot \dfrac{1}{2}}{4\,{\cdot}\,\!\left(-\dfrac{1}{4}\right) }=\dfrac{1}{2}\\ \end{eqnarray*}
The slope of the tangent line to the graph of 3x^{2}+4y^{2}=2x at the point \left( \dfrac{1}{2},-\dfrac{1}{4}\right) is \dfrac{1}{2}. An equation of the tangent line is \begin{eqnarray*} y+\dfrac{1}{4} &=&\dfrac{1}{2}\!\left( x-\dfrac{1}{2}\right) \\ y &=&\dfrac{1}{2}x-\dfrac{1}{2} \end{eqnarray*}
212
Figure 2 shows the graph of the ellipse 3x^{2}+4y^{2}=2x and the graph of the tangent line y=\dfrac{1}{2}x-\dfrac{1}{2} at the point \left( \dfrac{1}{2},-\dfrac{1}{4}\right) .
NOW WORK
EXAMPLE 4Using Implicit Differentiation
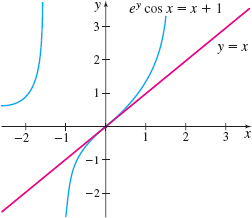
- (a) Find y^\prime if e^{y}\cos x=x+1.
- (b) Find an equation of the tangent line to the graph at the point (0,0) .
Solution (a) We use implicit differentiation: \begin{eqnarray*} \begin{array}{rl@{\qquad}l} \dfrac{d}{dx}( e^{y}\cos x) &= \dfrac{d}{dx}(x+1) \\ e^{y}\cdot \dfrac{d}{dx}( \cos x) +\left( \dfrac{d}{dx} e^{y}\right) \cdot \cos x &= 1 & {\color{#0066A7}{\hbox{Use the Product Rule.}}} \\ e^{y}( -\sin x) +e^{y}y^\prime \cdot \cos x &= 1 \\ ( e^{y}\cos x) y^\prime &= 1+e^{y}\sin x \\ y^\prime &= \dfrac{1+e^{y}\sin x}{e^{y}\cos x} \end{array} \end{eqnarray*}
(b) At the point (0,0) , the derivative y^\prime is \dfrac{1+e^{0}\sin 0}{e^{0}\cos 0}=\dfrac{1+1\cdot 0}{1\cdot 1}=1, so the slope of the tangent line to the graph at (0,0) is 1. An equation of the tangent line to the graph at the point (0,0) is y=x.
The graph of e^{y}\cos x=x+1 and the tangent line to the graph at (0,0) are shown in Figure 3.
2 Find Higher-Order Derivatives Using Implicit DifferentiationPrinted Page 212
Implicit differentiation can be used to find higher-order derivatives.
EXAMPLE 5Finding Higher-Order Derivatives
Use implicit differentiation to find y^\prime and y^{\prime\prime} if y^{2}-x^{2}=5. Express y^{\prime\prime} in terms of x and y.
Solution First, we assume there is a differentiable function y=f( x) that satisfies y^{2}-x^{2}=5. Now we find y^\prime .

provided y≠ 0.
213
Equations (3) and (4) both involve y^\prime . Either one can be used to find y^{\prime\prime} . We use (3) because it avoids differentiating a quotient. \begin{eqnarray*} \dfrac{d}{dx} ( 2yy^\prime -2x) &=&\dfrac{d}{dx}0 \nonumber\\ \dfrac{d}{dx} ( yy^\prime ) -\dfrac{d}{dx}x &=&0 \nonumber\\ y\cdot \dfrac{d}{dx}y^\prime +\left( \dfrac{d}{dx}y\right) y^\prime -1 &=&0 \nonumber\\ yy^{\prime\prime} +( y^\prime ) ^{2}-1 &=&0 \nonumber\\ y^{\prime\prime} &=&\dfrac{1-( y^\prime ) ^{2}}{y}\tag{5} \end{eqnarray*} provided y≠ 0. To express y^{\prime\prime} in terms of x and y, we use (4) and substitute for y^\prime in (5). 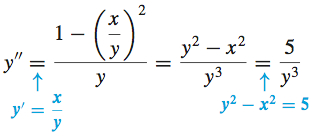
NOW WORK
3 Differentiate Functions with Rational ExponentsPrinted Page 213
In Section 2.4, we showed that the Simple Power Rule \dfrac{d}{dx}x^{n}=nx^{n-1} is true if the exponent n is any integer. We use implicit differentiation to extend this result for rational exponents.
THEOREM Power Rule for Rational Exponents
If y=x^{p/q}, where \dfrac{p}{q} is a rational number, then \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{y^\prime =\dfrac{d}{dx}x^{p/q}=\dfrac{p}{q}\cdot x^{\left(p/q\right) -1}}\tag{6} \end{equation*} provided that x^{p/q} and x^{(p/q) -1} are defined.
Proof
We begin with the function y=x^{p/q}, where p and q>0 are integers. Now, we raise both sides of the equation to the power q to obtain y^{q}=x^{p}
This is the implicit form of the function y=x^{p/q}. Assuming y is differentiable*, we can differentiate implicitly, obtaining \begin{eqnarray*} \frac{d}{dx}y^q &=& \frac{d}{dx} x^p\\ qy^{q-1}y^\prime &=& px^{p-1} \end{eqnarray*}
*In Problem 113, you are asked to show that y=x^{p/q} is differentiable.
214
Now solve for y^\prime. \begin{eqnarray*} && y^\prime =\dfrac{px^{p-1}}{qy^{q-1}}\underset{\underset{\color{#0066A7}{y=x^{p/q}}}{\color{#0066A7}{\uparrow}}}{=}\dfrac{p}{q}\cdot \dfrac{x^{p-1}}{( x^{p/q}) ^{q-1}}=\dfrac{p}{q} \cdot \dfrac{x^{p-1}}{x^{p-(p/q) }}=\dfrac{p}{q}\cdot x^{p-1-[ p-(p/q)] }=\dfrac{p}{q}\cdot x^{(p/q)-1}\\ \end{eqnarray*}
EXAMPLE 6Differentiating Functions with Rational Exponents
- (a) \dfrac{d}{dx}\sqrt{x}=\dfrac{d}{dx}x^{1/2}=\dfrac{1}{2} x^{( 1/2) -1}=\dfrac{1}{2}x^{-1/2}=\dfrac{1}{2x^{1/2}}=\dfrac{1}{2 \sqrt{x}}=\dfrac{\sqrt{x}}{2x}
- (b) \dfrac{d}{du}\sqrt[3]{u}=\dfrac{d}{du}u^{1/3}=\dfrac{1}{3} u^{-2/3}=\dfrac{1}{3\sqrt[3]{u^{2}}}=\dfrac{\sqrt[3]{u}}{3u}
- (c) \dfrac{d}{dx}x^{5/2}=\dfrac{5}{2}x^{3/2}
- (d) \dfrac{d}{ds}s^{-3/2}=-\dfrac{3}{2}s^{-5/2}=-\dfrac{3}{2s^{5/2}}
NOW WORK
THEOREM Power Rule for Functions
If u is a differentiable function of x and r is a rational number, then \bbox[5px, border:1px solid black, #F9F7ED] {\dfrac{d}{dx}[u(x)]^{r}=r[u(x)] ^{r-1}u^\prime (x)} provided u^{r} and u^{r-1} are defined.
EXAMPLE 7Differentiating Functions Using the Power Rule
- (a) \dfrac{d}{ds}(s^{3}-2s+1) ^{5/3}=\dfrac{5}{3} (s^{3}-2s+1) ^{2/3}\dfrac{d}{ds}(s^{3}-2s+1) = \dfrac{5}{3}(s^{3}-2s+1) ^{2/3}(3s^{2}-2)
- (b) \begin{align*} \dfrac{d}{dx}\sqrt[3]{x^{4}-3x+5} &=\dfrac{d}{dx}(x^{4}-3x+5) ^{1/3}=\dfrac{1}{3}(x^{4}-3x+5) ^{-2/3}\dfrac{d}{dx}(x^{4}-3x+5) \\&= \dfrac{4x^{3}-3}{3(x^{4}-3x+5)^{2/3}} \end{align*}
- (c) \begin{align*} \dfrac{d}{d\theta }[\tan (3\theta ) ] ^{-3/4}&=-\dfrac{3}{4}[\tan (3\theta ) ] ^{-7/4} \dfrac{d}{d\theta }\tan (3\theta ) = -\dfrac{3}{4}[\tan (3\theta ) ] ^{-7/4}\cdot \sec ^{2}(3\theta ) \cdot 3 \\&= -\dfrac{9\sec^2 (3\theta ) }{4[\tan (3\theta ) ] ^{7/4}} \end{align*}
NOW WORK
NEED TO REVIEW?
Inverse functions are discussed in Section P.4, pp. 32-37.
4 Find the Derivative of an Inverse FunctionPrinted Page 214
Suppose f is a function and g is its inverse function. Then g( f( x) ) =x for all x in the domain of f.
215
If both f and g are differentiable, we can differentiate both sides with respect to x using the Chain Rule. Then \begin{eqnarray*} && \dfrac{d}{dx}[g(f(x))] \underset{\underset{\underset{\underset{\color{#0066A7}{\hbox{on the left}}}{\color{#0066A7}{\hbox{Chain Rule}}}}{\color{#0066A7}{\hbox{Use the}}}}{\color{#0066A7}{\uparrow}}}{=} g^\prime (f(x)) \cdot f^\prime ( x) \underset{\underset{\underset{\color{#0066A7}{\hbox{on the right}}}{\color{#0066A7}{\hbox{\(\tfrac{d}{dx}x=1\)}}}}{\color{#0066A7}{\uparrow}}}{=} 1\\ \\ \end{eqnarray*}
Since the product of the derivatives is never 0, each function has a nonzero derivative on its domain.
Conversely, if a one-to-one function has a nonzero derivative, then its inverse function also has a nonzero derivative as stated in the following theorem.
THEOREM Derivative of an Inverse Function
Let y=f( x) and x=g( y) be inverse functions. Suppose f is differentiable on an open interval containing x_{0} and y_{0}=f( x_{0}) . If f^\prime ( x_{0}) ≠ 0, then g is differentiable at y_{0}=f( x_{0}) and \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{d}{dy}g(y_{0}) =g^\prime (y_{0}) =\dfrac{1}{f^\prime (x_{0})}}\tag{7} \end{equation*} where the notation \dfrac{d}{dy}g( y_{0})=g^\prime(y_{0}) means the value of \dfrac{d}{dy}g( y) at y_{0}, and the notation f^\prime ( x_{0}) means the value of f^\prime ( x) at x_{0}.
In Leibniz notation, formula (7) has the simple form \bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{dx}{dy}=\dfrac{1}{\dfrac{dy}{dx}}}
We have two comments to make about this theorem, which is proved in Appendix B:
- If y_{0}=f( x_{0}) and f^\prime ( x_{0}) ≠ 0 exists, then \dfrac{d}{dy}g( y) exists at y_{0}.
- It gives formula ( 7) for finding \dfrac{d}{dy}g(y) at y_{0} without knowing a formula for g=f^{-1}, provided we can find x_{0} and f^\prime ( x_{0}) .
EXAMPLE 8Finding the Derivative of an Inverse Function
The function f( x) =x^{5}+x has an inverse function g. Find g^\prime (2) .
Solution Using (7) with y_{0}=2, we get g^\prime (2) =\dfrac{1}{f^\prime (x_{0})}\qquad \hbox{where}\ 2=f( x_{0})
A solution of the equation f( x_{0}) =x_{0}^{5}+x_{0}=2 is x_{0}=1. Since f^\prime ( x) =5x^{4}+1, then f^\prime (x_{0})= f^\prime (1) =6 and g^\prime (2) =\dfrac{1}{f^\prime (1) }=\dfrac{1}{6}
Observe in Example 8 that the derivative of the inverse function g at 2 was evaluated without actually knowing a formula for g.
NOW WORK
5 Differentiate the Inverse Trigonometric FunctionsPrinted Page 216
216
Table 1 lists the inverse trigonometric functions and their domains.
NEED TO REVIEW?
Inverse trigonometric functions are discussed in Section P.7, pp. 58-61.
| f | Restricted Domain | f^{-1} | Domain |
|---|---|---|---|
| f(x) =\sin x | \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right] | f^{-1}( x) =\sin ^{-1}x | [-1,1] |
| f(x) =\cos x | [0,\pi] | f^{-1}( x) =\cos ^{-1}x | [-1,1] |
| f(x) =\tan x | \left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right) | f^{-1}( x) =\tan ^{-1}x | (-\infty ,\infty) |
| f(x) =\csc x | \left(-\pi, -\dfrac{\pi}{2}\right]\cup \left(0, \dfrac{\pi}{2}\right] | f^{-1}( x) =\csc ^{-1}x | |x| ≥ 1 |
| f(x) =\sec x | \left[0, \dfrac{\pi}{2}\right)\cup \left[\pi, \dfrac{3\pi}{2}\right) | f^{-1}(x) =\sec ^{-1}x | |x| ≥ 1 |
| f(x) =\cot x | (0,\;\pi) | f^{-1}( x) =\cot ^{-1}x | (-\infty ,\infty) |
To find the derivative of y=\sin ^{-1}x, -1≤ x≤ 1, -\dfrac{\pi }{2}≤ y≤ \dfrac{\pi }{2}, we write \sin y=x and differentiate implicitly with respect to x. \begin{eqnarray*} \dfrac{d}{dx}\sin y &=&\dfrac{d}{dx}x \\ \cos y\cdot \dfrac{dy}{dx} &=&1 \\ \dfrac{dy}{dx} &=&\dfrac{1}{\cos y} \end{eqnarray*} provided \cos y≠ 0. Since \cos y=0 if y=-\dfrac{\pi }{2} or y=\dfrac{\pi }{2}, we exclude these values. Then \dfrac{d}{dx}\sin^{-1} x=\dfrac{1}{\cos y}, -\dfrac{\pi }{2}< y< \dfrac{\pi }{2}. Now, if -\dfrac{\pi }{2}< y< \dfrac{\pi }{2}, then \cos y> 0. Using a Pythagorean identity, we have \begin{eqnarray*} \cos ^{2}y &=&1-\sin ^{2}y \\ \cos y &\underset{\underset{\color{#0066A7}{\hbox{\(\cos y>0\)}}}{\color{#0066A7}{\uparrow}}}{=}& \sqrt{1-\sin ^{2}y} \underset{\underset{\color{#0066A7}{\hbox{\(\sin y=x\)}}}{\color{#0066A7}{\uparrow}}}{=} {\sqrt{1-x^{2}}}\\ \end{eqnarray*}
THEOREM Derivative of y=\sin ^{-1}x
The derivative of the inverse sine function y=\sin ^{-1}x is \bbox[5px, border:1px solid black, #F9F7ED]{ y^\prime = \dfrac{d}{dx}\sin ^{-1}x=\dfrac{1}{\sqrt{1-x^{2}}} \qquad -1< x< 1}
EXAMPLE 9Using the Chain Rule with the Inverse Sine Function
Find y^\prime if:
(a) y=\sin ^{-1}(4x^{2}) \quad (b) y=e^{\sin ^{-1}x}
Solution (a) If y=\sin ^{-1}u and u=4x^{2}, then \dfrac{dy}{du}=\dfrac{1}{\sqrt{1-u^{2}}} and \dfrac{du}{dx}=8x. By the Chain Rule, \begin{eqnarray*} && y^\prime =\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot \dfrac{du}{dx}=\left( \dfrac{1}{ \sqrt{1-u^{2}}}\right) (8x) = \dfrac{8x}{\sqrt{1-16x^{4}}}\qquad {\color{#0066A7}{\hbox{\(u=4x^{2}\)}}} \end{eqnarray*}
217
(b) If y=e^{u} and u=\sin ^{-1}x, then \dfrac{dy}{du}=e^{u} and \dfrac{du}{dx}=\dfrac{1}{\sqrt{1-x^{2}}}. By the Chain Rule, \begin{eqnarray*} && y^\prime =\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot \dfrac{du}{dx}=e^{u}\cdot \dfrac{ 1}{\sqrt{1-x^{2}}} \underset{\underset{\color{#0066A7}{\hbox{\(u=\sin ^{-1}x\)}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{ e^{\sin ^{-1}x}}{\sqrt{1-x^{2}}} \\ \end{eqnarray*}
NOW WORK
To derive a formula for the derivative of y\,{=}\,\tan^{-1}x, -\infty\,{< }\,x\,{< }\,\infty , -\dfrac{\pi }{2}\,{< }\,y\,{<}\,\dfrac{\pi }{2}, we write \tan y=x and differentiate with respect to x. Then \begin{eqnarray*} \dfrac{d}{dx}\tan y &=&\dfrac{d}{dx}x \\ \sec ^{2}y\dfrac{dy}{dx} &=&1 \\ \dfrac{dy}{dx} &=&\dfrac{1}{\sec ^{2}y} \end{eqnarray*}
Since -\dfrac{\pi }{2}< y< \dfrac{\pi }{2}, then \sec y≠ 0.
Now we use the Pythagorean identity \sec ^{2}y=1+\tan ^{2}y, and substitute x=\tan y. Then y^\prime =\dfrac{d}{dx}\tan ^{-1}x=\dfrac{1}{1+x^{2}}
THEOREM Derivative of {y=\tan ^{-1}x}
The derivative of the inverse tangent function y=\tan ^{-1}x is \bbox[5px, border:1px solid black, #F9F7ED]{ y^\prime =\dfrac{d}{dx}\tan ^{-1}x=\dfrac{1}{1+x^{2}}}
The domain of y^\prime is all real numbers.
EXAMPLE 10Using the Chain Rule with the Inverse Tangent Function
Find y^\prime if:
(a) y=\tan ^{-1}( 4x) \quad (b) y=\sin ( \tan ^{-1}x)
Solution (a) Let y=\tan ^{-1}u and u=4x. Then \dfrac{dy}{du}=\dfrac{1}{1+u^{2}} and \dfrac{du}{dx}=4. By the Chain Rule, y^\prime =\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot \dfrac{du}{dx}=\dfrac{1}{1+u^{2}} \cdot 4=\dfrac{4}{1+16x^{2}}
(b) Let y=\sin u and u=\tan ^{-1}x. Then \dfrac{dy}{du}=\cos u and \dfrac{du}{dx}=\dfrac{1}{1+x^{2}}. By the Chain Rule, y^\prime =\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot \dfrac{du}{dx}=\cos u\cdot \dfrac{1}{1+x^{2}}=\dfrac{\cos ( \tan ^{-1}x) }{1+x^{2}}
NOW WORK
Finally to find the derivative of y=\sec ^{-1}x, \vert x\vert ≥ 1, 0≤ y< \dfrac{\pi }{2} or \pi ≤ y< \dfrac{3\pi }{2}, we write x=\sec y and use implicit differentiation. \begin{eqnarray*} \dfrac{d}{dx}x &=&\dfrac{d}{dx}\sec y \\ 1 &=&\sec y\tan y\dfrac{dy}{dx} \end{eqnarray*}
218
We can solve for \dfrac{dy}{dx} provided \sec y≠ 0 and \tan y≠ 0, or equivalently, y≠ 0 and y≠ \pi. That is, \dfrac{dy}{dx}=\dfrac{1}{\sec y\tan y},\qquad \hbox{provided}\; 0< y< \dfrac{\pi }{2} \ \hbox{or}\ \pi < y< \dfrac{3\pi }{2}.
With these restrictions on y, \tan y>0.* Now we use the Pythagorean identity 1+\tan ^{2}y=\sec ^{2}y. Then \tan y = \sqrt{\sec^2 y-1} and \begin{eqnarray*} && \dfrac{1}{\sec y\tan y}=\dfrac{1}{\sec y\sqrt{\sec ^{2}y-1}} \underset{\underset{\color{#0066A7}{\hbox{\(\sec y=x\)}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{1}{x\sqrt{x^{2}-1}}\\ \end{eqnarray*}
THEOREM Derivative of {y=\sec ^{-1}x}
The derivative of the inverse secant function y=\sec ^{-1}x is \bbox[5px, border:1px solid black, #F9F7ED]{ y^\prime =\dfrac{d}{dx}\sec ^{-1}x=\dfrac{1}{x\sqrt{x^{2}-1}}\qquad \vert x\vert > 1 }
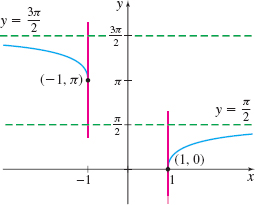
Notice that y=\sec ^{-1}x is not differentiable when x=\pm 1. In fact, as Figure 4 shows, at the points \left( -1,\pi \right) and (1,0), the graph of y=\sec ^{-1}x has vertical tangent lines.
The formulas for the derivatives of the three remaining inverse trigonometric functions can be obtained using the following identities:
- Since \cos ^{-1}x=\dfrac{\pi }{2}-\sin ^{-1}x, then \dfrac{d}{dx} \cos ^{-1}x=-\dfrac{1}{\sqrt{1-x^{2}}}, where \vert x\vert\,{< }\,1.
- Since \cot ^{-1}x=\dfrac{\pi }{2}-\tan ^{-1}x, then \dfrac{d}{dx} \cot ^{-1}x=-\dfrac{1}{1+x^{2}}, where -\infty\,{< }\,x\,{< }\,\infty .
- Since \csc ^{-1}x=\dfrac{\pi }{2}-\sec ^{-1}x, then \dfrac{d}{dx} \csc ^{-1}x=-\dfrac{1}{x\sqrt{x^{2}-1}}, where \vert x\vert\,{>}\,1.
*The restricted domain of y=\sec x was chosen as \left\{x|0≤ x< \dfrac{\pi }{2}\hbox{ or } \pi ≤ x< \dfrac{3\pi }{2}\right\} so that \tan x > 0.