2.4 Differentiating the Product and the Quotient of Two Functions; Higher-Order DerivativesPrinted Page 173
173
In this section, we obtain formulas for differentiating products and quotients of functions. As it turns out, the formulas are not what we might expect. The derivative of the product of two functions is not the product of their derivatives, and the derivative of the quotient of two functions is not the quotient of their derivatives.
1 Differentiate the Product of Two FunctionsPrinted Page 173
Consider the two functions f(x)=2x and g(x)=x3. Both are differentiable, and their derivatives are f′(x)=2 and g′(x)=3x2. Form the product F(x)=f(x)g(x)=(2x)(x3)=2x4
Now find F′ using the Constant Multiple Rule and the Simple Power Rule. F′(x)=2(4x3)=8x3
Notice that f′(x)g′(x)=(2)(3x2)=6x2 is not equal to F′(x)=ddx[f(x)g(x)]=8x3. We conclude that the derivative of a product of two functions is not the product of their derivatives.
To find the derivative of the product of two differentiable functions f and g, we let F(x)=f(x)g(x) and use the definition of a derivative, namely, F′(x)=lim
We can express F’ in an equivalent form that contains the difference quotients for f and g, by subtracting and adding f( x+h)g( x) to the numerator.
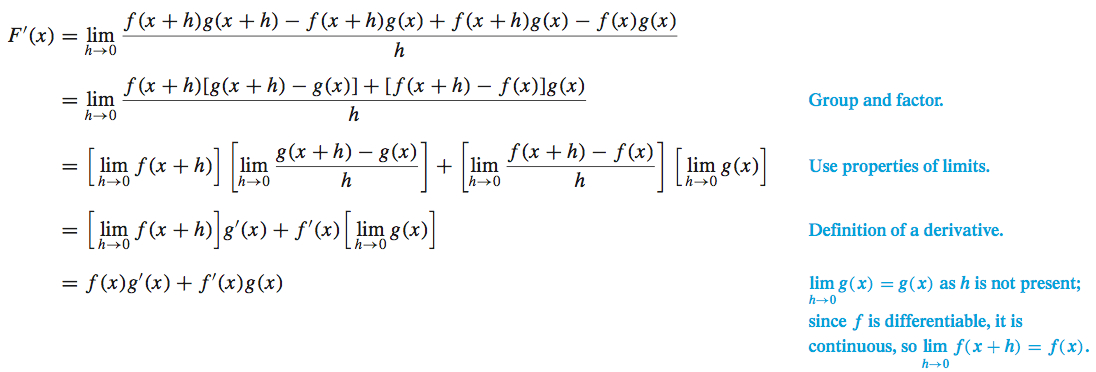
174
We have established the following formula.
IN WORDS
The derivative of the product of two differentiable functions equals the first function times the derivative of the second function plus the derivative of the first function times the second function. That is, (fg)' =f (g^\prime ) + ( f^\prime ) g.
THEOREM Product Rule
If f and g are differentiable functions and if F(x) =f(x) g(x), then F is differentiable, and the derivative of the product F is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] {F' (x) =[f(x) g(x)]' =f(x) g' (x) +f' (x) g(x)}}
In Leibniz notation, the Product Rule takes the form \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] {\dfrac{d}{dx}F( x) =\dfrac{d}{dx}[ f( x) g( x) ] =f( x) \left[ \dfrac{d}{ dx}g( x) \right] +\left[ \dfrac{d}{dx}f( x) \right] g( x)}}
EXAMPLE 1Differentiating the Product of Two Functions
Find y^\prime if y=( 1+x^{2}) e^{x}\!.
Solution The function y is the product of two functions: a polynomial, f( x) =1+x^{2}, and the exponential function g( x) =e^{x}. By the Product Rule, \begin{eqnarray*} &&y^\prime =\frac{d}{dx}[(1+x^{2}) e^{x}] {=} (1+x^{2}) \left[ \frac{d}{dx}e^{x}\right] +\left[\frac{d}{dx}(1+x^{2})\right] e^{x}=( 1+x^{2}) e^{x}+2xe^{x}\\[-6.4pt] &&\hspace{4.9pc}\underset{\color{#0066A7}{\scriptsize \hbox{Product Rule}}}{\color{#0066A7}{\uparrow}} \end{eqnarray*}
At this point, we have found the derivative, but it is customary to simplify the answer. Then \begin{eqnarray*} &&y\prime {=} ( 1+x^{2}+2x) e^{x} {=} ( x+1) ^{2}e^{x}\\[-6.4pt] &&\hspace{-0.7pc}\underset{\color{#0066A7}{\scriptsize \hbox{Factor out \(e^{x}\).}}}{\color{#0066A7}{\uparrow }}\hspace{2.5pc}\underset{\color{#0066A7}{\scriptsize \hbox{Factor}.}}{\color{#0066A7}{\uparrow }} \end{eqnarray*}
NOW WORK
Do not use the Product Rule unnecessarily! When one of the factors is a constant, use the Constant Multiple Rule. For example, it is easier to work \dfrac{d}{dx}[ 5( x^{2}+1) ] =5\dfrac{d}{dx}( x^{2}+1) =5\cdot 2x=10x
than it is to work \dfrac{d}{dx}[ 5( x^{2}+1) ] =5\dfrac{d}{dx}( x^{2}+1) +\left[ \dfrac{d}{dx}5\right] ( x^{2}+1) =5\cdot 2x+0\cdot ( x^{2}+1) =10x
Also, it is easier to simplify f( x) =x^{2}( 4x-3) before finding the derivative. That is, it is easier to work \dfrac{d}{dx}[ x^{2}( 4x-3) ] =\dfrac{d}{dx}( 4x^{3}-3x^{2}) =12x^{2}-6x
than it is use the Product Rule \begin{eqnarray*} \dfrac{d}{dx}[ x^{2}( 4x-3) ] &=&x^{2}\dfrac{d}{dx} ( 4x-3) +\left( \dfrac{d}{dx}x^{2}\right) ( 4x-3) =( x^{2}) ( 4) +( 2x) ( 4x-3)\\[5pt] &=&4x^{2}+8x^{2}-6x=12x^{2}-6x \end{eqnarray*}
EXAMPLE 2Differentiating a Product in Two Ways
Find the derivative of F(v)=( 5v^{2}-v+1) ( v^{3}-1) in two ways:
- (a) By using the Product Rule.
- (b) By multiplying the factors of the function before finding its derivative.
175
Solution
(a) F is the product of the two functions f(v) =5v^{2}-v+1 and g( v) =v^{3}-1. Using the Product Rule, we get \begin{eqnarray*} F^\prime ( v) &=& ( 5v^{2}-v+1) \left[\dfrac{d}{dv}(v^{3}-1)\right]+\left[\dfrac{d}{dv}(5v^{2}-v+1)\right]( v^{3}-1)\\[5pt] &=&(5v^{2}-v+1) (3v^{2}) +(10v-1) (v^{3}-1)\\[5pt] &=&15v^{4}-3v^{3}+3v^{2}+10v^{4}-10v-v^{3}+1\\[5pt] &=&25v^{4}-4v^{3}+3v^{2}-10v+1 \end{eqnarray*}
(b) Here, we multiply the factors of F before differentiating. F\left( v\right) =( 5v^{2}-v+1) ( v^{3}-1) =5v^{5}-v^{4}+v^{3}-5v^{2}+v-1
Then F' ( v) =25v^{4}-4v^{3}+3v^{2}-10v+1
Notice that the derivative is the same whether you differentiate and then simplify, or whether you multiply the factors and then differentiate. Use the approach that you find easier.
NOW WORK
2 Differentiate the Quotient of Two FunctionsPrinted Page 175
The derivative of the quotient of two functions is not equal to the quotient of their derivatives. Instead, the derivative of the quotient of two functions is found using the Quotient Rule.
THEOREM Quotient Rule
If two functions f and g are differentiable and if F(x) =\dfrac{f(x) }{g(x) }, g(x)\neq 0, then F is differentiable, and the derivative of the quotient F is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] F' (x) =\left[ \dfrac{f(x) }{g(x) }\right] ^{\prime }=\dfrac{f^\prime (x) g(x) -f(x) g^\prime ( x) }{\left[ g( x) \right] ^{2}} }
IN WORDS
The derivative of a quotient of two functions is the derivative of the numerator times the denominator, minus the numerator times the derivative of the denominator, all divided by the denominator squared. That is, \left( \dfrac{f}{g}\right)^{\!\!\prime} = \dfrac{f'g - fg'}{ g^{2}}.
In Leibniz notation, the Quotient Rule takes the form \bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{d}{dx}F( x) = \dfrac{d}{dx}\left[ \dfrac{f( x) }{g( x) }\right] =\dfrac{\left[ \dfrac{d}{ dx}f( x) \right] g( x) -f( x) \left[ \dfrac{d}{dx}g( x) \right] }{[ g( x) ] ^{2}}}
PROOF
We use the definition of a derivative to find F' (x). \begin{eqnarray*} F' ( x) &=&\lim\limits_{h\rightarrow 0}\dfrac{F( x+h) -F( x) }{h} \underset{\underset{\color{#0066A7}{F( x) =\dfrac{f(x) }{g(x) }}}{\color{#0066A7}{\uparrow }}}{=} \lim\limits_{h \rightarrow 0}\dfrac{\dfrac{f( x+h) }{g( x+h) }-\dfrac{ f(x) }{g( x) }}{h}\\ &=&\lim\limits_{h\rightarrow 0}\dfrac{ f(x+h) g(x) -f(x) g(x+h) }{ h[g( x+h) g( x) ] } \end{eqnarray*}
We write F’ in an equivalent form that contains the difference quotients for f and g by subtracting and adding f(x) g(x) to the numerator. F' ( x) =\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) g( x) -f( x) g( x) +f( x) g( x) -f( x) g( x+h) }{h[ g( x+h) g( x) ] }
176
Now we group and factor the numerator. \begin{eqnarray*} F' ( x) &=&\lim\limits_{h\rightarrow 0}\dfrac{[ f( x+h) -f( x) ] g( x) -f( x) [ g( x+h) -g( x) ] }{h[ g( x+h) g( x) ] }\\[5pt] \notag \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{\left[ \dfrac{f( x+h) -f( x) }{h}\right] g( x) -f( x) \left[ \dfrac{g( x+h) -g( x) }{h}\right] }{g( x+h) g( x) }\\[5pt] \notag \\ &=&\dfrac{\lim\limits_{h\rightarrow 0}\left[ \dfrac{f( x+h) -f( x) }{h}\right] \cdot \lim\limits_{h\rightarrow 0}g( x) -\lim\limits_{h\rightarrow 0}f( x) \cdot \lim\limits_{h\rightarrow 0}\left[ \dfrac{g( x+h) -g( x) }{h}\right] }{\lim\limits_{h\rightarrow 0}g( x+h) \cdot \lim\limits_{h\rightarrow 0}g( x) }\\[5pt] \notag \\ &=&\dfrac{f^\prime ( x) g( x) -f( x) g^\prime ( x) }{[ g( x) ] ^{2}} \end{eqnarray*}
RECALL
Since g is differentiable, it is continuous; so, \lim\limits_{h\rightarrow 0}{ g} ( x+h ) =g (x) .
EXAMPLE 3Differentiating the Quotient of Two Functions
Find y^\prime if y=\dfrac{x^{2}+1}{2x-3}.
Solution The function y is the quotient of f( x) =x^{2}+1 and g( x) =2x-3. Using the Quotient Rule, we have \begin{eqnarray*} y^\prime &=&\dfrac{d}{dx}\!\left(\! \dfrac{x^{2}+1}{2x-3}\!\right) =\dfrac{\left[ \dfrac{d}{dx}( x^{2}+1) \right]\! ( 2x-3) -(x^{2}+1) \left[ \dfrac{d}{dx} \! ( 2x-3) \right] }{( 2x-3) ^{2}} \\[5pt] &=&\dfrac{( 2x) ( 2x-3) -( x^{2}+1) (2) }{( 2x-3) ^{2}}=\dfrac{4x^{2}-6x-2x^{2}-2}{( 2x-3) ^{2}}=\dfrac{2x^{2}-6x-2}{( 2x-3) ^{2}} \end{eqnarray*}
provided x\neq \dfrac{3}{2}.
NOW WORK
COROLLARY Derivative of the Reciprocal of a Function
IN WORDS
The derivative of the reciprocal of a function is the negative of the derivative of the denominator divided by the square of the denominator. That is, \left( \dfrac{1}{g}\right) ^{\!\!\prime} = - \dfrac{g'}{g^2}.
If a function g is differentiable, then \bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{d}{dx}\!\left[ \dfrac{1}{g( x) }\right] =-\dfrac{ \dfrac{d}{dx}g( x) }{\left[ g( x) \right] ^{2}}=- \dfrac{g^\prime ( x) }{\left[ g( x) \right] ^{2}} }\tag{1}
provided g( x) \neq 0.
The proof of the corollary is left as an exercise. (See Problem 98.)
EXAMPLE 4Differentiating the Reciprocal of a Function
- (a) \dfrac{d}{dx}\!\left( \dfrac{1}{x^{2}+x}\right) {=} -\dfrac{\dfrac{d}{dx}( x^{2}+x) }{( x^{2}+x) ^{2}}=-\dfrac{2x+1}{( x^{2}+x) ^{2}}\\[-7pt] \hspace{3.7pc} \underset{\color{#0066A7}{\scriptsize \hbox{Use (1).}}}{\color{#0066A7}{\uparrow}}
- (b) \dfrac{d}{dx}e^{-x}=\dfrac{d}{dx}\!\left( \dfrac{1}{e^{x}}\right) {=} -\dfrac{\dfrac{d }{dx}e^{x}}{( e^{x}) ^{2}}=-\dfrac{e^{x}}{e^{2x}}=-\dfrac{1}{e^{x} }=-e^{-x}\\[-6.4pt] \hspace{5.4pc}\underset{\color{#0066A7}{\scriptsize \hbox{Use (1).}}}{\color{#0066A7}{\uparrow}}
NOW WORK
177
Notice that the derivative of the reciprocal of a function f is not the reciprocal of the derivative. That is, \dfrac{d}{dx}\!\left[ \dfrac{1}{f(x)}\right] ≠ \dfrac{1}{f^\prime (x)}
The rule for the derivative of the reciprocal of a function allows us to extend the Simple Power Rule to all integers. Here is the proof.
Suppose n is a negative integer and x ≠ 0. Then, m=-n is a positive integer, and \begin{eqnarray*} y^\prime\! &=& \dfrac{d}{dx}x^{n}=\dfrac{d}{dx}\dfrac{1}{x^{m}}\underset{\underset{\color{#0066A7}{\text{Use (1).}}}{\color{#0066A7}{\uparrow}}}{=}-\dfrac{\dfrac{d}{dx}( x^{m}) }{( x^{m}) ^{2}}\underset{\underset{\underset{\color{#0066A7}{\text{Power Rule}}}{\color{#0066A7}{\text{Simple}}}}{\color{#0066A7}{\uparrow}}}{=}-\dfrac{mx^{m-1}}{x^{2m}} =-mx^{m-1-2m}{=}-mx^{-m-1}\underset{\underset{\underset{\color{#0066A7}{~n=-m.}}{{\color{#0066A7}{\text{Substitute}}}}}{\color{#0066A7}{\uparrow}}}{=}nx^{n-1} \end{eqnarray*}
THEOREM Power Rule
The derivative of y=x^{n}, where n any integer, is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] y^\prime =\dfrac{d}{dx}x^{n}=nx^{n-1} }
EXAMPLE 5Differentiating Using the Power Rule
- (a) \dfrac{d}{dx}x^{-1}=-x^{-2}=-\dfrac{1}{x^{2}}
- (b) \dfrac{d}{du}\!\left( \dfrac{1}{u^{2}}\right) =\dfrac{d}{du} u^{-2}=-2u^{-3}=-\dfrac{2}{u^{3}}
- (c) \dfrac{d}{ds}\!\left( \dfrac{4}{s^{5}}\right) =4\dfrac{d}{ds} s^{-5}=4\cdot \left( -5\right) s^{-6}=-20s^{-6}=-\dfrac{20}{s^{6}}
NOW WORK
EXAMPLE 6Using the Power Rule in Electrical Engineering
Ohm’s Law states that the current I running through a wire is inversely proportional to the resistance R in the wire and can be written as I=\dfrac{ V}{R}, where V is the voltage. Find the rate of change of I with respect to R when V=12 volts.
Solution The rate of change of I with respect to R is the derivative \dfrac{dI}{dR}. We write Ohm’s Law with V=12 as I=\dfrac{V}{R }=12R^{-1} and use the Power Rule. \dfrac{dI}{dR}=\dfrac{d}{dR}( 12R^{-1}) =12\cdot \dfrac{d}{dR} R^{-1}=12( -1R^{-2}) =-\dfrac{12}{R^{2}}
The minus sign in \dfrac{dI}{dR} indicates that the current I decreases as the resistance R in the wire increases.
NOW WORK
3 Find Higher-Order DerivativesPrinted Page 177
Since the derivative f^\prime is a function, it makes sense to ask about the derivative of f^\prime. The derivative (if there is one) of f^\prime is also a function called the second derivative of f and denoted by f'', read, “f double prime.”
178
By continuing in this fashion, we can find the third derivative of f, the fourth derivative of f, and so on, provided that these derivatives exist. Collectively, these are called higher-order derivatives.
Leibniz notation can be used for higher-order derivatives as well. Table 3 summarizes the notation for higher-order derivatives.
| Prime Notation | Leibniz Notation | |||
|---|---|---|---|---|
| First Derivative | y^\prime | f^\prime (x) | \dfrac{dy}{dx} | \dfrac{d}{dx} f(x) |
| Second Derivative | y'' | f'' (x) | \dfrac{d^{2}y}{dx^{2}} | \dfrac{d^{2}}{dx^{2}} f( x) |
| Third Derivative | y''' | f''' ( x) | \dfrac{d^{3}y}{dx^{3}} | \dfrac{d^{3}}{dx^{3}} f( x) |
| Fourth Derivative | y^{( 4)} | f^{( 4) }( x) | \dfrac{d^{4}y}{dx^{4}} | \dfrac{d^{4}}{dx^{4}} f( x) |
| ⋮ | ||||
| nth Derivative | y^{(n)} | f^{(n)}(x) | \dfrac{d^{n}y}{dx^{n}} | \dfrac{d^{n}}{dx^{n}} f( x) |
EXAMPLE 7Finding Higher-Order Derivatives of a Power Function
Find the second, third, and fourth derivatives of y=2x^{3}.
Solution Since y is a power function, we use the Simple Power Rule and the Constant Multiple Rule to find each derivative. The first derivative is y^\prime =\dfrac{d}{dx}( 2x^{3}) = 2\cdot \dfrac{d}{dx}x^{3}=2\cdot 3x^{2}=6x^{2}
The next three derivatives are
y''=\dfrac{d^{2}}{dx^{2}}( 2x^{3}) =\dfrac{d}{dx}( 6x^{2}) =6\cdot \dfrac{d}{dx}x^{2}=6\cdot 2x=12x\\[5pt]
y'''=\dfrac{d^{3}}{dx^{3}}( 2x^{3}) =\dfrac{d}{dx}( 12x) =12
y^{(4)}=\dfrac{d^{4}}{dx^{4}}( 2x^{3}) =\dfrac{d}{dx}12=0
All derivatives of this function f of order 4 or more equal 0. This result can be generalized. For a power function f of degree n, where n is a positive integer,
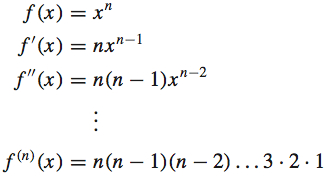
The nth-order derivative of f( x) =x^{n} is a constant function, so all derivatives of order greater than n equal 0.
It follows from this discussion that the nth derivative of a polynomial of degree n is a constant and that all derivatives of order n+1 and higher equal 0.
NOTE
If n >1 is an integer, the product n\cdot ( n-1 ) \cdot ( n-2 ) \cdot \cdots \cdot 3\cdot 2\cdot 1 is often written n! and is read, “n factorial.” The factorial symbol n! means 0!=1, 1!=1, and n!=1\cdot 2\cdot 3\cdot \cdots \cdot ( n-1 ) \cdot n, where n>1.
NOW WORK
179
EXAMPLE 8Finding Higher-Order Derivatives
Find the second and third derivatives of y=( 1+x^{2})e^{x}.
Solution In Example 1, we found that y^\prime =(1+x^{2}) e^{x}+2xe^{x}=(x^{2}+2x+1) e^{x}. To find y'', we use the Product Rule with y^\prime. \begin{eqnarray*} y'' &=&\dfrac{d}{dx}[ (x^{2}+2x+1) e^{x}] {=}(x^{2}+2x+1) \left( \dfrac{d}{dx}e^{x}\right) +\left[ \dfrac{d}{dx} ( x^{2}+2x+1) \right] e^{x} \\[-6.4pt] &&\hspace{4.8pc}\underset{\color{#0066A7}{\scriptsize \hbox{Product Rule}}}{\color{#0066A7}{\uparrow }}\\ &=&(x^{2}+2x+1) e^{x}+( 2x+2) e^{x}=(x^{2}+4x+3) e^{x}\\[5pt] y''' &=&\dfrac{d}{dx}[ ( x^{2}+4x+3) e^{x}] {=}(x^{2}+4x+3) \dfrac{d}{dx}e^{x}+\left[ \dfrac{d}{dx}(x^{2}+4x+3) \right] e^{x}\\[-6.4pt] &&\hspace{4.8pc}\underset{\color{#0066A7}{\scriptsize \hbox{Product Rule}}}{\color{#0066A7}{\uparrow }}\\ &=&( x^{2}+4x+3) e^{x}+\left( 2x+4\right) e^{x}=(x^{2}+6x+7) e^{x} \end{eqnarray*}
NOW WORK
4 Work with AccelerationPrinted Page 179
For an object in rectilinear motion whose distance s from the origin at time t is s=s(t), the derivative s' ( t) has a physical interpretation as the velocity of the object. The second derivative s'', which is the rate of change of the velocity s', is called acceleration.
DEFINITION Acceleration
When the distance s of an object from the origin at time t is given by a function s=s( t), the first derivative \dfrac{ds}{dt} is the velocity v=v( t) of the object at time t.
The acceleration a=a( t) of an object at time t is defined as the rate of change of velocity with respect to time. That is, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] a=a( t) =\dfrac{dv}{dt}=\dfrac{d}{dt}v=\dfrac{d}{dt} \! \left( \dfrac{ds}{dt}\right) =\dfrac{d^{2}s}{dt^{2}} }
IN WORDS
Acceleration is the second derivative of distance with respect to time.
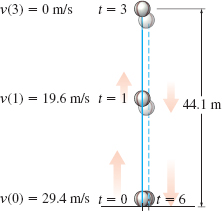
EXAMPLE 9Analyzing Vertical Motion
A ball is propelled vertically upward from the ground with an initial velocity of 29.4 meters per second. The height s (in meters) of the ball above the ground is approximately s=s( t) =-4.9t^{2}+29.4t, where t is the number of seconds that elapse from the moment the ball is released.
- (a) What is the velocity of the ball at time t? What is its velocity at t=1second?
- (b) When will the ball reach its maximum height?
- (c) What is the maximum height the ball reaches?
- (d) What is the acceleration of the ball at any time t?
- (e) How long is the ball in the air?
- (f) What is the velocity of the ball upon impact with the ground?
- (g) What is the total distance traveled by the ball?
Solution (a) Since s=-4.9t^{2}+29.4t, then \begin{eqnarray*} v&=&v( t) ={\dfrac{ds}{dt}}=-9.8t+29.4\\[5pt] v(1) &=&-9.8+29.4=19.6 \end{eqnarray*}
At t=1, the velocity of the ball is 19.6m/s.
180
(b) The ball reaches its maximum height when v( t) =0. \begin{eqnarray*} v( t) &=&-9.8t+29.4=0 \\ 9.8t &=& 29.4 \\ t &=&3 \end{eqnarray*}
The ball reaches its maximum height after 3 seconds.
(c) The maximum height is s=s(3) =-4.9(3^{2})+29.4(3)=44.1
The maximum height of the ball is 44.1 m.
(d) The acceleration of the ball at any time t is a=a( t) ={\dfrac{d^{2}s}{dt^{2}}}=\dfrac{dv}{dt}=\dfrac{d}{dt}( -9.8t+29.4) =-9.8m/s^{2}
(e) There are two ways to answer the question “How long is the ball in the air?” First way: Since it takes 3s for the ball to reach its maximum altitude, it follows that it will take another 3s to reach the ground, for a total time of 6s in the air. Second way: When the ball reaches the ground, s=s( t) =0. Solve for t: \begin{eqnarray*} s( t) &=&-4.9t^{2}+29.4t=0\\[4pt] && t (-4.9t + 29.4) =0\\[4pt] t&=&0\qquad \hbox{or}\qquad t=\frac{29.4}{4.9}=6 \end{eqnarray*}
The ball is at ground level at t=0 and at t=6, so the ball is in the air for 6 seconds.
(f) Upon impact with the ground, t=6s. So the velocity is v( 6) =(-9.8)(6)+29.4=-29.4
Upon impact the direction of the ball is downward, and its speed is 29.4m/s.
(g) The total distance traveled by the ball is s(3) +s(3) =2~s(3) =2( 44.1) =88.2{m}
See Figure 25 for an illustration.
NOW WORK
NOTE
The Earth is not perfectly round; it bulges sightly at the equator, and its mass is not distributed uniformly. As a result, the acceleration of a freely falling body varies slightly.
In Example 9, the acceleration of the ball is constant. In fact, acceleration is the same for all falling objects at the same location, provided air resistance is not taken into account. In the sixteenth century, Galileo (1564–1642) discovered this by experimentation.* He also found that all falling bodies obey the law stating that the distance s they fall when dropped is proportional to the square of the time t it takes to fall that distance, and that the constant of proportionality c is the same for all objects. That is, s=-ct^{2}
The velocity v of the falling object is v=\dfrac{ds}{dt}=\dfrac{d}{dt}( -ct^{2}) =-2ct
181
and its acceleration a is a=\dfrac{dv}{dt}=\dfrac{d^{2}s}{dt^{2}}=-2c
which is a constant. Usually, we denote the constant 2c by g so c=\dfrac{1}{2}g. Then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] {a=-g\qquad v=-gt\qquad s=-\dfrac{1}{2}gt^{2}} }
The number g is called the acceleration due to gravity. For our planet, g is approximately 32 ft/s{^2}, or 9.8 m/s {^2}. On the planet Jupiter, g \approx 26.0m/s{^2}, and on our moon, g\approx 1.60m/units{^2}.
*In a famous legend, Galileo dropped a feather and a rock from the top of the Leaning Tower of Pisa, to show that the acceleration due to gravity is constant. He expected them to fall together, but he failed to account for air resistance that slowed the feather. In July 1971 Apollo 15 Astronaut David Scott repeated the experiment on the moon, where there is no air resistance. He dropped a hammer and a falcon feather from his shoulder height. Both hit the moon’s surface at the same time. A video of this experiment may be found at the NASA website.