13.2 Assess Your UnderstandingPrinted Page 877
Concepts and Vocabulary
True or False If F is differentiable at a point P0=(x0,y0,z0) on the surface F(x,y,z)=0, and if {\bf \boldsymbol \nabla }F(x_{0},y_{0},z_{0})\neq \mathbf{0}, then the surface has a tangent plane at P_{0}.
True
True or False The normal line to the surface F(x,y,z)=0 at a point P_{0}=(x_{0},y_{0},z_{0}) is in the direction of the gradient {\boldsymbol \nabla }F(x_{0},y_{0},z_{0}), provided {\boldsymbol \nabla }F(x_{0},y_{0},z_{0})\neq \mathbf{0}.
True
Skill Building
In Problems 3–6, find an equation of the tangent plane to each surface at the given point.
z=10-2x^{2}-y^{2} at ( 0,2,6)
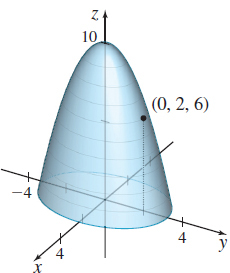
4y+z = 14
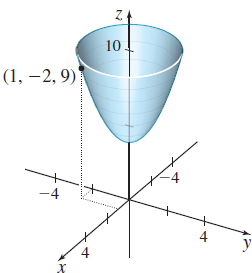
z=4+x^{2}+y^{2} at ( 1,-2,9)
878
z=4x^{2}+9y^{2} at ( 1,1,13)
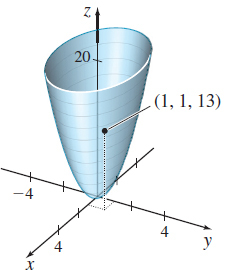
8x + 18y - z = 13
z=\sqrt{x^{2}+3y^{2}} at ( 1,1,2)
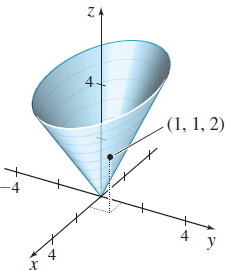
In Problems 7–18:
- (a) Find an equation of the tangent plane to each surface at the given point.
- (b) Find symmetric equations of the normal line to each surface at the given point.
x^{2}+y^{2}+z^{2}=14 at (1,-2,3)
- (a) x - 2y + 3z = 14
- (b) {{x - 1} \over 1} = {{y + 2} \over { - 2}} = {{z - 3} \over 3}
2x^{2}+3y^{2}+z^{2}=12 at (2,1,-1)
4x^{2}+y^{2}-2z^{2}=3 at (1,1,-1)
- (a) 4x+y + 2z = 3
- (b) {{x - 1} \over 4} = {{y - 1} \over 1} = {{z + 1} \over 2}
z^{2}=x^{2}+3y^{2} at (1,-1,-2)
z=x^{2}+y^{2} at (-2,1,5)
- (a) 4x-2y+z =-5
- (b) {{x + 2} \over { - 4}} = {{y - 1} \over 2} = {{z - 5} \over { - 1}}
z=2x^{2}-3y^{2} at (2,1,5)
2x^{2}-y^{2}=z at (1,0,2)
- (a) 4x - z = 2
- (b) {{x - 1} \over 4} = {{z - 2} \over { - 1}}; y = { 0}
x^{2}+y^{2}-2z^{2}=-13 at (2,1,3)
x^{2}-3y^{2}-4z^{2}=2 at (3,1,1)
- (a) 3x - 3y - 4z = 2
- (b) {{x - 3} \over 3} = {{y - 1} \over { - 3}} = {{z - 1} \over { - 4}}
x^{2}+2y^{2}-5z^{2}=4 at (1,2,1)
f(x,y)=\ln ( \sec (x^{2}+y^{2})) at \left( \sqrt{\dfrac{\pi }{8}},\sqrt{\dfrac{\pi }{8}},\ln \sqrt{2}\right)
- (a) x\sqrt {{\pi \over 2}} + y\sqrt {{\pi \over 2}} - z = {\pi \over 2} - \ln \sqrt{2}
- (b) {{x - \sqrt {{\pi \over 8}} } \over {\sqrt {{\pi \over 2}} }} = {{y - \sqrt {{\pi \over 8}} } \over {\sqrt {{\pi \over 2}} }} = {{z - \ln \sqrt{2}} \over { - 1}}
f(x,y)=\dfrac{x^{2}-y^{2}}{x^{2}+y^{2}} at \left(1,2, -\dfrac{3}{5}\right)
In Problems 19–22:
- (a) Find an equation of the tangent plane to each surface at the given point.
- (b) Find symmetric equations of the normal line to each surface at the given point.
- (c)
 Use technology to graph each surface and the tangent plane to the surface at the given point.
Use technology to graph each surface and the tangent plane to the surface at the given point.
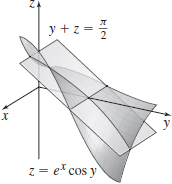
z=e^{x}\cos y at \left( 0,\dfrac{\pi}{2},0\right)
- (a) y+z={\pi \over 2}
- (b) {{y - {\pi \over 2}} \over { - 1}} = {z \over { - 1}}; x = { 0}
- (c)
z=\ln (x^{2}+y^{2}) at (1,-1,\ln 2)
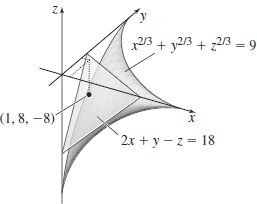
x^{2/3}+y^{2/3}+z^{2/3}=9 at (1,8,-8)
- (a) 2x+y - z = 18
- (b) {{x - 1} \over 2} = {{y - 8} \over 1} = {{z + 8} \over { - 1}}
- (c)
x^{1/2}+y^{1/2}+z^{1/2}=6 at (1,4,9)
Applications and Extensions
Show that the same results would have been obtained in Example 1 by solving the equation x^{2}+y^{2}-z^{2}-24=0 for z and using the function z=f(x,y)=\sqrt{x^{2}+y^{2}-24} whose graph is the part of the hyperboloid lying above the xy-plane.
See Student Solutions Manual.
Show that the same results would have been obtained in Example 2 by solving the equation x^{2}+y^{2}-z^{2}-24=0 for z and using the function z=f(x,y)=\sqrt{x^{2}+y^{2}-24} whose graph is the part of the hyperboloid lying above the xy-plane.
In Problems 25–30, determine the point(s) on the surface of z=f( x,y) at which the tangent plane is parallel to the xy-plane.
z=6x-4y-x^{2}-2y^{2}
The tangent plane is parallel to the xy-plane at (x, y, z) = ( 3, -1, 11 ).
z=4x-2y+x^{2}+y^{2}
z=x^{2}+2xy+y^{2}
The tangent plane is parallel to the xy-plane for all (x, y, z) such that y =-x and z = 0.
z=x^{2}-3xy+y^{2}
z=2x^{4}-y^{2}-x^{2}-2y
The tangent plane is parallel to the xy-plane at (x, y, z) = (0, -1, 1 ), \left(\dfrac{1}{2}, -1,\dfrac{7}{8}\right), and \left(-\dfrac{1}{2},-1,\dfrac{7}{8}\right).
z=x^{2}+y^{4}-4y^{2}-2x
Solar Panel An engineer is building experimental, dome- shaped living quarters 4\,\rm{m} high and modeled by the function z=4-x^{2}-y^{2}. She wants to bolt a flat solar panel to the dome at the point (1,1,2). In what direction should the engineer drill?
The engineer should drill in the direction 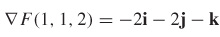 .
.
- (a) Two surfaces are said to be tangent at a common point \boldsymbol P_{0} if each has the same tangent plane at \boldsymbol P_{0}. Show that the surfaces x^{2}+z^{2}+4y=0 and x^{2}+y^{2}+z^{2}-6z+7=0 are tangent at the point (0,-1,2).
- (b)
 Graph each surface.
Graph each surface.
- (a) Show that the surfaces x^{2}+y^{2}+z^{2}=1 and x^{2}+y^{2}-z^{2}=1 are tangent at every point of intersection.
- (b)
 Graph each surface.
Graph each surface.
- (a) See Student Solutions Manual.
- (b)
- (a) Two surfaces are orthogonal at a common point \boldsymbol P_{0} if their normal lines at \boldsymbol P_{0} are orthogonal. Show that the surfaces x^{2}+y^{2}+z^{2}=4 and x^{2}+y^{2}-z^{2}=0 are orthogonal at (0,\sqrt{2} ,\sqrt{2}). In fact, show that the surfaces are orthogonal at every point of intersection.
- (b)
 Graph each surface.
Graph each surface.
Normal Lines of a Sphere Show that the normal lines of a sphere x^{2}+y^{2}+z^{2}=R^{2} pass through the center of the sphere.
See Student Solutions Manual.
Normal Line of a Sphere Let P_{0}=(x_{0},y_{0},z_{0}) be a point on the sphere x^{2}+y^{2}+z^{2}=R^{2}. Show that the normal line to the sphere at P_{0} passes through the point (-x_{0},-y_{0},-z_{0}).
Tangent Plane Find equations of the tangent plane and normal line to \sin (x+y)+\sin (y+z)=1 at the point \left( 0,\dfrac{\pi }{ 2},\dfrac{\pi }{2}\right) .
The equation of the tangent plane is y+z=\pi. The symmetric equations for the normal are {{y - {\pi \over 2}} \over { - 1}} = {{z - {\pi \over 2}} \over { - 1}},\;x = 0.
Tangent Plane to an Ellipsoid Find the points on the surface \dfrac{x^{2}}{9}+\dfrac{y^{2}}{4}+\dfrac{z^{2}}{36}=1, where the tangent plane is parallel to the plane 2x-3y+z=4.
Tangent Plane to a Cylinder Show that the tangent plane to the cylinder x^{2}+y^{2}=a^{2} at the point (x_{0},y_{0},z_{0}) is given by the equation x_{0}x+y_{0}y=a^{2}.
See Student Solutions Manual.
Tangent Plane to a Cone Show that the tangent plane to the cone \dfrac{z^{2}}{c^{2}}=\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}} at the point (x_{0},y_{0},z_{0})\neq (0,0,0) is given by the equation \dfrac{ z_{0}}{c^{2}}z=\dfrac{x_{0}}{a^{2}}x+\dfrac{y_{0}}{b^{2}}y. Why must the point of tangency be different from the origin?
879
Show that at any point, the sum of the intercepts on the coordinate axes of the tangent plane to the surface x^{1/2}+y^{1/2}+z^{1/2}=a^{1/2}, a>0, is a constant.
See Student Solutions Manual.
Challenge Problems
Tangent Line Find an equation of the tangent line to the curve of intersection of the surfaces x\sin (yz) =1 and ze^{y^{2}-x^{2}}=\dfrac{\pi }{2} at the point \left( 1,1,\dfrac{\pi }{2} \right) .
Find equations of the tangent plane and normal line to (yz)^{xz}=16 at the point (2,1,2).
An equation of the tangent plane is (\ln 2) x + 2 y + (1 + \ln 2) z = 4 (1+ \ln 2). Symmetric equations of the normal line are {{x - 2} \over {\ln 2}} = {{y - 1} \over 2} = {{z - 2} \over {1 + \ln 2}}.
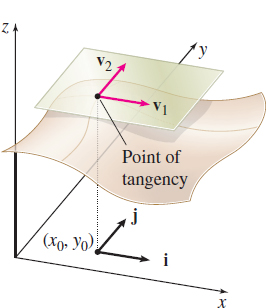
Consider the tangent plane to the graph of a differentiable function z=f(x,y) at a point (x_{0},y_{0}). Suppose \mathbf{v}_{1} is a tangent vector on the plane whose \mathbf{j} component is 0 and \mathbf{v}_{2} is a tangent vector on the plane whose \mathbf{i} component is 0. Must \mathbf{ v}_{1} and \mathbf{v}_{2} be at right angles? See the figure.