13.4 Lagrange MultipliersPrinted Page 891
891
OBJECTIVES
When you finish this section, you should be able to:
Many applications require finding maximum (or minimum) values of a function when a certain condition or constraint is present. For example, we might want to maximize the volume of a box using a fixed amount of material (its surface area). A solution to such problems can be obtained using Lagrange multipliers.
We begin by finding a minimum value subject to one constraint.
EXAMPLE 1Solve an Optimization Problem
Find the point in the first quadrant on the hyperbola xy=4 where the value of z=12x+3y is a minimum. What is the minimum value?
Solution We seek the minimum value of z=12x+3y subject to the condition, or constraint, that x and y satisfy the equation xy=4. Since x>0 and y>0, we can express this as a problem in one variable by solving xy=4 for y and substituting y=4x in the expression z=12x+3y. z=12x+3y=↑y=4x12x+12xx>0
Then dzdx=12−12x2=12x2−12x2x>0
The critical numbers of z are −1 and 1. We exclude x=−1, since x>0. To examine x=1, we apply the Second Derivative Test. Since d2zdx2=24x3>0 for x=1, we conclude that z has a minimum when x=1 and y=4x=4. The minimum value of z is 24 at the point (1,4) on the hyperbola.
NEED TO REVIEW?
The Second Derivative Test is discussed in Section 4.4, pp. 291-292.
In Example 1, we solved the problem by eliminating the variable y and treating the problem as a minimum problem in one variable. Sometimes, however, it is not easy, or perhaps it is impossible, to eliminate a variable. Then the Method of Lagrange Multipliers is useful. Before we use the method, let's look at a geometric rationale.
A Geometric Rationale for the Method of Lagrange Multipliers
Consider Example 1 again. We want to minimize the function z=f(x,y)=12x+3y, subject to the constraint g(x,y)=xy−4=0. The graph of g(x,y)=xy−4=0 is a curve (a hyperbola) in the xy-plane. We are interested in finding the smallest value of z=f(x,y), where (x,y) is a point in the first quadrant on the graph of g(x,y)=0.
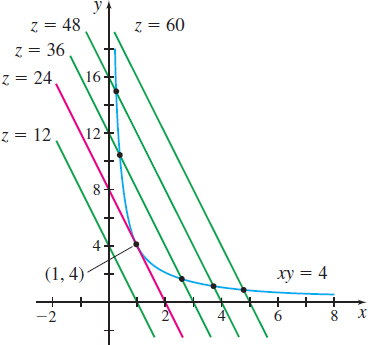
Figure 21 shows the level curves of z=12x+3y. On a given level curve, the value of z is fixed. We are seeking the smallest z that coincides with the hyperbola xy=4. We observe in Figure 21 that the minimum value of z occurs precisely at the point where the line 12x+3y=24 is tangent to the graph of the hyperbola xy=4. At this point, the two curves have a common tangent line, so they must have the same normal line. Since the gradient gives the direction of the normal line to a curve, it follows that ∇f is parallel to ∇g. That is, there is a scalar λ≠0, so that ∇f=λ∇gandg(x,y)=0
892
This discussion leads to the following result.
THEOREM Lagrange's Theorem
Let f and g be functions of two variables with continuous partial derivatives at every point of some open set containing the smooth curve g(x,y)=0. Suppose that f, when restricted to points on the curve g(x,y)=0, has a local extremum at the point (x0,y0) and that ∇g(x0,y0)≠0. Then there is a number λ for which \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ {\nabla }f(x_{0},y_{0})=\lambda {\nabla }g(x_{0},y_{0}) }}

Proof
Express the smooth curve C defined by g(x,y)=0 as a parametric equation in vector form \mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}. Define the function s(t)=f(x(t),y(t)) and choose t_{0} so that x_{0}=x(t_{0}), y_{0}=y(t_{0}). Now since f has a local extremum at the point (x_{0},y_{0}), the extreme value is given by \begin{equation*} s(t_{0})=f(x(t_{0}),y(t_{0}))=f( x_{0},y_{0}) \end{equation*}
Then s' (t_{0})=0. By Chain Rule I, \begin{eqnarray*} s' (t_{0}) &=&f_{x}(x_{0},y_{0})x'(t_{0})+f_{y}(x_{0},y_{0})y' (t_{0}) \qquad {\color{#0066A7}{\hbox{\(\tfrac{ds}{dt}=\tfrac{\partial s}{\partial x} \tfrac{dx}{dt}+\tfrac{\partial s}{\partial y}\tfrac{dy}{dt}\)}}}\\ &=&{\nabla }f(x_{0},y_{0})\,{\cdot}\, \mathbf{r}^{\prime }(t_{0}) \qquad\qquad\qquad \enspace \enspace \enspace {\color{#0066A7}{\hbox{Definition of the gradient}}}\\ &=&0 \end{eqnarray*}
If {\nabla }f(x_{0},y_{0})\neq \mathbf{0}, it is orthogonal to \mathbf{r}' (t_{0}), which is a tangent vector to C at (x_{0},y_{0}). Since the gradient is normal to the level curve at ( x_{0},y_{0}) , the vector {\nabla }g(x_{0},y_{0}) is also orthogonal to \mathbf{r}' (t_{0}). If {\nabla }f(x_{0},y_{0})=\mathbf{0}, then let \lambda =0. Thus, in every case, there is a number \lambda for which {\nabla }f(x_{0},y_{0})=\lambda {\nabla } g(x_{0},y_{0}).
ORIGINS
Joseph-Louis Lagrange (1736–1813), a.k.a. Giuseppe Lodovico Lagrangia, was a self-taught mathematician and astronomer. He was born and began his career teaching in Turin, Italy, but later moved first to Berlin and then to Paris, where he held prestigious positions at the Berlin Academy and Acad\smale mie des Sciences. After the French Revolution (1789), Lagrange was named the first professor of analysis at the École Polytechnique, in Paris. Lagrange is one of 72 names of mathematicians, engineers, and scientists inscribed on the Eiffel Tower.
The number \lambda in the equations {\nabla }f(x,y)=\lambda {\nabla }g(x,y) is called a Lagrange multiplier. Since {\nabla }f=\lambda {\nabla }g, we have f_{x}\mathbf{i}+f_{y}\mathbf{j}=\lambda ( g_{x}\mathbf{i}+g_{y}\mathbf{j}), so that f_{x}(x,y)=\lambda g_{x}(x,y) and f_{y}(x,y)=\lambda g_{y}(x,y). These equations and the equation g(x,y)=0 form a system of three equations in the three unknowns x,y, and \lambda. \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ f_{x}(x,y)=\lambda g_{x}(x,y)\qquad f_{y}(x,y)=\lambda g_{y}(x,y)\qquad g(x,y)=0 }}
A solution (x_{0},y_{0}) of the system of equations is called a test point, since it is a candidate for the desired extrema. The maximum and minimum values, if they exist, are found by choosing the largest and smallest values of z=f(x,y) at the test points.
1 Use Lagrange Multipliers for an Optimization Problem with One ConstraintPrinted Page 892
EXAMPLE 2Solving Example 1 Using Lagrange Multipliers
Find the point in the first quadrant on the hyperbola xy=4, where the value of z=12x+3y is a minimum. What is the minimum value?
Solution We can reword the problem to read as follows: Find the minimum value of z=f(x,y)=12x+3y subject to the condition xy=4, where x>0 and y>0.
The test points satisfy the equations {\nabla }f(x,y)=\lambda {\nabla }g(x,y)\qquad g(x,y)=xy-4=0\qquad x>0\quad y>0
where \lambda is a number.
893
Solve the system of equations \left\{\begin{array}{l} 12 &=&\lambda y \qquad \enspace{\color{#0066A7}{\hbox{\(f_{x} (x,y)=\lambda g_{x} (x,y)\)}}}\\ 3 &=&\lambda x \qquad \enspace {\color{#0066A7}{\hbox{\(f_{y} (x,y)=\lambda g_{y} (x,y)\)}}}\\ xy-4 &=&0 \qquad \enspace \enspace {\color{#0066A7}{\hspace{.3pc}\hbox{\(g(x,y)=0\)}}} \end{array}\right.
NOTE
In eliminating \lambda , we use the fact that \lambda \neq 0 since {\nabla }f\neq \mathbf{0}.
Eliminating \lambda from the first two equations results in y=4x, so the third equation becomes \begin{eqnarray*} &\qquad\qquad \enspace 4x^{2}-4=0 \\[2pt] &x=1 \qquad \enspace \enspace \hbox{or} \enspace \enspace \enspace x=-1 \end{eqnarray*}
Since x>0, we ignore x=-1. When x=1, then y=4, so the only test point is (1,4). The corresponding minimum value of z=12x+3y is z=24.
NOW WORK
Steps for Using Lagrange Multipliers
Step 1 Express the problem in the following form: Find the maximum (or minimum) value of z=f( x,y) subject to the constraint g( x,y) =0.
Step 2 Check that the functions f and g satisfy Lagrange's Theorem.
Step 3 Solve the equations {\nabla }f( x,y) =\lambda {\nabla }g( x,y) and g( x,y) =0 for the test points by solving the system of equations \left\{\begin{array}{rcl} f_{x}( x,y) &=&\lambda g_{x}( x,y)\\ f_{y}( x,y) &=&\lambda g_{y}( x,y)\\ g( x,y) &=&0\end{array}\right.
Step 4 Evaluate z=f( x,y) at each test point found in Step 3. Choose the maximum (or minimum) value of z.
EXAMPLE 3Using Lagrange Multipliers
Find the maximum and minimum values of z=f(x,y)=3x-y+1 subject to the constraint 3x^{2}+y^{2}=9.
Solution We use the steps for Lagrange multipliers:
Step 1 The problem is expressed in the required form.
Step 2 The functions f and g( x,y) =3x^{2}+y^{2}-9=0 each have continuous partial derivatives.
Step 3 Solve the system of equations \left\{\begin{array}{rcl} 3&=&6\lambda x & \qquad {\color{#0066A7}{\hbox{\(f_{x}(x,y) =\lambda g_{x}(x,y)\)}}}\\ -1&=&2\lambda y & \qquad {\color{#0066A7}{\hbox{\(f_{y}(x,y) =\lambda g_{y}(x,y)\)}}}\\ 3x^{2}+y^{2}-9&=&0 & \qquad {\color{#0066A7}{\hspace{.3pc}\hbox{\(g(x,y) =0\)}}} \end{array}\right.
From the first two equations, we find that x=\dfrac{1}{2\lambda } and y=-\dfrac{1}{2\lambda } from which x=-y. Substituting into the third equation, we have \begin{eqnarray*} 4x^2&=&9\\[4pt] x&=&\pm \dfrac{3}{2} \end{eqnarray*}
Then x=\pm \dfrac{3}{2}, y=\mp \dfrac{3}{2}, and the test points are \left( \dfrac{3}{2},-\dfrac{3}{2}\right) and \left( -\dfrac{3}{2},\dfrac{3}{2}\right).
894
Step 4 The values of z corresponding to the test points are z=\dfrac{9}{2}+\dfrac{3}{2}+1=7 and z=-\dfrac{9}{2}-\dfrac{3}{2}+1=-5. The maximum value of z is 7 and the minimum value is -5.
NOW WORK
EXAMPLE 4Using Lagrange Multipliers to Find Absolute Extrema
Find the absolute maximum and absolute minimum of f(x,y)=x^{2}+y^{2}+4x-4y+3 subject to x^{2}+y^{2}\leq 2.
Solution From the Extreme Value Theorem, f has both an absolute maximum and an absolute minimum on the closed, bounded set x^{2}+y^{2}\leq 2. We begin by finding any critical points. \begin{equation*} \begin{array}{rcl@{\qquad}rrcl} f_{x}=2x+4&=&0 & f_{y}=2y-4&=&0\\ x&=&-2 & y&=&2 \end{array}\end{equation*}
The point ( -2,2) lies outside the disk x^{2}+y^{2}\leq 2, so f has no relevant critical points. The extrema must occur on the boundary of the domain, that is, on the curve x^{2}+y^{2}=2. To find the extrema, we use Lagrange multipliers.
Step 1 Using g(x,y)=x^{2}+y^{2}-2=0 as the constraint, the problem is expressed in the required form.
Step 2 The functions f and g( x,y) =x^{2}+y^{2}-2=0 each have continuous partial derivatives.
Step 3 We solve the system of equations {\nabla }f( x,y) =\lambda {\nabla }g( x,y) and g( x,y) =0. \left\{ \begin{array}{rcl@{\qquad}l} 2x+4&=&2\lambda x \qquad \enspace{\color{#0066A7}{\hbox{\(f_{x}(x,y) =\lambda g_{x}(x,y)\)}}}\\ 2y-4&=&2\lambda y \qquad \enspace{\color{#0066A7}{\hbox{\(f_{y}(x,y) =\lambda g_{y}(x,y)\)}}}\\ x^{2}+y^{2}&=&2 \qquad \enspace \enspace \enspace \enspace {\color{#0066A7}{\hbox{\(g(x,y) =0\)}}} \end{array}\right.
We eliminate \lambda from the first two equations. \begin{eqnarray*} 2x+4&=&2x\lambda \qquad \enspace 2y-4&=&2y\lambda\\ \lambda &=& \dfrac{2x+4}{2x} & \lambda &=&\dfrac{2y-4}{2y}\\ \lambda &=& 1+\dfrac{2}{x} & \lambda &=& 1-\dfrac{2}{y} \end{eqnarray*}
Then 1+\dfrac{2}{x}=1-\dfrac{2}{y}, so y=-x.
If we substitute y=-x into the third equation x^{2}+y^{2}=2, we find 2x^{2}=2. Then x=\pm 1 and y=\mp 1. There are two test points: (1,-1) and (-1,1).
Step 4 We evaluate z=f( x,y) at each test point. \begin{eqnarray*} f(1,-1)&=&13 \qquad {\color{#0066A7}{\hbox{Maximum value}}}\\ f(-1,1)&=&-3 \qquad {\color{#0066A7}{\hbox{Minimum value}}} \end{eqnarray*}
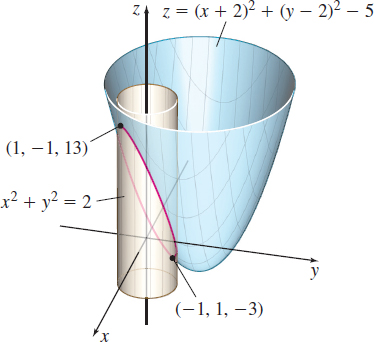
The cylinder x^{2}+y^{2} =2 and the elliptic paraboloid z=( x+2) ^{2}+( y-2) ^{2}-5, are shown in Figure 22.
NOW WORK
895
Lagrange multipliers can be used for functions of three variables. The extreme values of w=f(x,y,z) subject to the constraint g(x,y,z)=0, if they exist, occur at the solutions (x,y,z) of the system of equations. \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ {\nabla }f(x,y,z)=\lambda {\nabla }g(x,y,z)\qquad \hbox{and} \qquad g(x,y,z)=0 }}
These equations form a system of four equations in the four unknowns x, y, z, and \lambda.
EXAMPLE 5Using Lagrange Multipliers with a Function of Three Variables
A container in the shape of a rectangular box is open on top and has a fixed volume of 12 m^3. The material used to make the bottom of the container costs $3 per square meter, while the material used for the sides costs $1 per square meter. What dimensions will minimize the cost of material?

Solution Let x be the width of the container, y its depth, and z its height. Then its volume is xyz=12. The cost function C=C(x,y,z), which is to be minimized, is C(x,y,z) =3xy+2xz+2yz
We use Lagrange multipliers.
Step 1 The objective is to minimize C subject to the constraint g(x,y,z)=xyz-12=0.
Step 2 The functions C and g each have continuous partial derivatives.
Step 3 We solve the system of equations {\nabla }C(x,y,z) =\lambda {\nabla }g(x,y,z) and g(x,y,z) =0. \left\{\begin{array}{lllll} 3y+2z &=&\lambda yz \qquad {\color{#0066A7}{\hbox{\(C_{x}(x,y,z) =\lambda g_{x}( x,y,z)\)}}} \enspace \enspace {\color{#0066A7}{\hbox{(\(1\))}}}\\ 3x+2z &=&\lambda xz \qquad {\color{#0066A7}{\hbox{\(C_{y}(x,y,z) =\lambda g_{y}( x,y,z)\)}}} \enspace \enspace {\color{#0066A7}{\hbox{(\(2\))}}}\\ 2x+2y &=&\lambda xy \qquad {\color{#0066A7}{\hbox{\(C_{z}(x,y,z) =\lambda g_{z}( x,y,z)\)}}} \enspace \enspace {\color{#0066A7}{\hbox{(\(3\))}}}\\ xyz-12 &=&0 \qquad \enspace \enspace \enspace {\color{#0066A7}{\hbox{\(g( x,y,z) =0\)}}}\quad \enspace \qquad \enspace \enspace \enspace{\color{#0066A7}{\hbox{(\(4\))}}} \end{array}\right.
Now we use the facts that x>0, y>0, and z>0 to solve the first three equations for \lambda, obtaining \lambda =\dfrac{3}{z}+\frac{2}{y}\enspace {\color{#0066A7}{\hbox{(\(5\))}}} \qquad \lambda =\frac{3}{z}+\frac{2}{x}\enspace {\color{#0066A7}{\hbox{(\(6\))}}} \qquad \lambda =\dfrac{2}{y}+\frac{2}{x}\enspace {\color{#0066A7}{\hbox{(\(7\))}}}
From these, we find that \begin{eqnarray*} y &=&x \qquad \enspace\enspace\enspace {\color{#0066A7}{\hbox{From equations (5) and (6)}}}\\ z &=&\dfrac{3}{2}x \qquad \enspace \enspace {\color{#0066A7}{\hbox{From equations (5) and (7)}}} \end{eqnarray*}
If we substitute these two equations into xyz-12=0, we find \[ \begin{eqnarray*} xyz-12& =&0 \\[4pt] x( x) \left( \dfrac{3}{2}x\right) -12& =&0 \\[4pt] \frac{3}{2}x^{3}& =&12 \\[4pt] x& =&2 \end{eqnarray*}
Then y=2, z=3, and the test point is (2,2,3).
Step 4 The dimensions of the container that minimize the cost are 2 m by 2 m by 3 m. The minimum cost is C(2,2,3)=3 ( 2) ( 2) +2 ( 2) (3) +2 ( 2) ( 3) =$36.
NOW WORK
2 Use Lagrange Multipliers for an Optimization Problem with Two ConstraintsPrinted Page 896
896
Lagrange multipliers can be used to solve problems involving more than one constraint. In the two-constraint situation, we seek the extreme values of a function w=f(x,y,z) subject to two constraints g(x,y,z)=0 and h(x,y,z)=0. The extreme values of f, if they exist, occur at solutions (x,y,z) of the system of five equations containing the five variables x,y,z,\lambda_1 and \lambda_2. \left\{\begin{eqnarray*} {\nabla }f(x,y,z) &=&\lambda _{1}{\nabla }g(x,y,z)+\lambda _{2}{\nabla }h(x,y,z)\\ g(x,y,z) &=&0\\ h(x,y,z) &=&0 \end{eqnarray*}\right.
where \lambda _{1} and \lambda _{2} are Lagrange multipliers.
EXAMPLE 6Using Lagrange Multipliers with Two Constraints
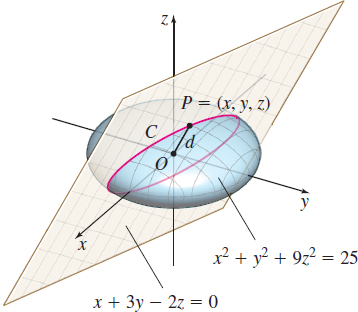
Find the points of intersection of the ellipsoid x^{2}+y^{2}+9z^{2}=25 and the plane x+3y-2z=0 that are farthest from the origin. Also find the points that are closest to the origin.
Solution See Figure 23.
Let C be the curve formed by intersecting the ellipsoid and the plane, and let P=(x,y,z) be a point on C. We use the steps for Lagrange multipliers.
Step 1 The function to be optimized is the distance d from P to the origin: d=f(x,y,z)=\sqrt{x^{2}+y^{2}+z^{2}}
subject to the constraints \begin{eqnarray*} g(x,y,z) &=&x^{2}+y^{2}+9z^{2}-25=0 \qquad \enspace \enspace {\color{#0066A7}{\hbox{The point must be on the ellipsoid.}}}\\ h(x,y,z) &=&x+3y-2z=0 \qquad \qquad \qquad {\color{#0066A7}{\hbox{The point must be on the plane.}}} \end{eqnarray*}
Step 2 The functions f, g, and h are each functions of three variables, and each has continuous partial derivatives at every point of some open set containing the smooth curve defined by g(x,y,z)=0 and h(x,y,z)=0.
Step 3 We introduce two Lagrange multipliers and solve the system of equations {\nabla }f(x,y,z)=\lambda _{1}{\nabla }g(x,y,z)+\lambda _{2}{\nabla }h(x,y,z), g(x,y,z)=0, and h(x,y,z)=0. 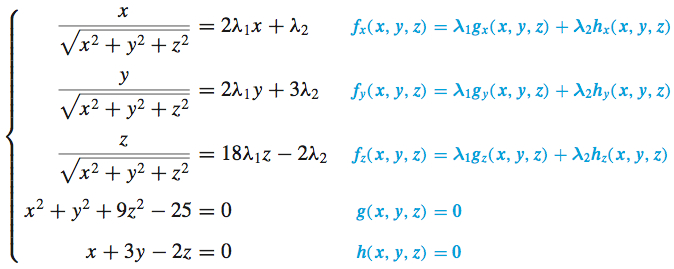
Eliminating \lambda _{1} and \lambda _{2} from the first three equations, we have two possibilities: z=0 or y=3x. Using each of these equations with the constraints
897
x^{2}+y^{2}+9z^{2}- 25=0 and x+3y-2z=0 results in the following: \begin{eqnarray*} z&=&0{:} & \left( -\dfrac{15}{\sqrt{10}},\dfrac{5}{\sqrt{10}},0\right) \qquad \qquad \enspace \enspace \enspace {\color{#0066A7}{\hbox{5 units from the origin}}}\\ &&& \left( \dfrac{15}{\sqrt{10}},-\dfrac{5}{\sqrt{10}},0\right) \qquad \qquad \enspace \enspace \enspace {\color{#0066A7}{\hbox{5 units from the origin}}}\\ y&=&3x{:} & \left( \dfrac{5}{\sqrt{235}},\dfrac{15}{\sqrt{235}},\dfrac{25}{\sqrt{235}}\right) \qquad \enspace {\color{#0066A7}{\hbox{\(\sqrt{\dfrac{875}{235}}\approx 1.930\) units from the origin}}}\\ &&& \left( -\dfrac{5}{\sqrt{235}},-\dfrac{15}{\sqrt{235}},-\dfrac{25}{\sqrt{235}}\right) \enspace \enspace {\color{#0066A7}{\hbox{\(\sqrt{\dfrac{875}{235}}\approx\) 1.930 units from the origin}}} \end{eqnarray*}
The points \left( -\dfrac{15}{\sqrt{10}},\dfrac{5}{\sqrt{10}},0\right) and \left( \dfrac{15}{\sqrt{10}},-\dfrac{5}{\sqrt{10}},0\right) are farthest from the origin, and the points \left( \dfrac{5}{\sqrt{235}},\dfrac{15}{\sqrt{235}},\dfrac{25}{\sqrt{235}}\right) and \left( -\dfrac{5}{\sqrt{235}},-\dfrac{15}{\sqrt{235}},-\dfrac{25}{\sqrt{235}}\right) are closest to the origin. Since the intersection of the ellipsoid and the plane is an ellipse, the points we have found are the endpoints of the major and minor axes of this ellipse.