14.8 Triple Integrals Using Spherical Coordinates
OBJECTIVES
When you finish this section, you should be able to:
- Convert rectangular coordinates to spherical coordinates (p. 956)
- Find a triple integral using spherical coordinates (p. 958)
As we have seen in Section 14.7, there are times when it is easier to find a triple integral using an alternate coordinate system. When a triple integral involves all or a portion of a sphere centered at the origin or all or a portion of a cone, converting the problem to spherical coordinates often reduces the effort needed to find the integral.
1 Convert Rectangular Coordinates to Spherical Coordinates
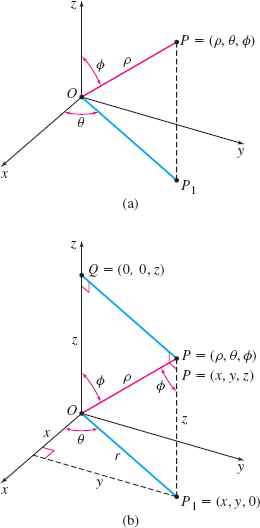
Suppose \(P\) is a point in space. If \(P\) is not at the origin, we define the three numbers \(\rho ,\) \(\ \theta \) , and \(\phi \) as:
- \(\rho =\left\vert {\it OP}\right\vert \) is the distance from the origin to the point \(P\).
- \(\theta \) is the angle between the positive \(x\)-axis and \({\it OP}_{1},\) where \(P_{1}\) is the projection of \(P\) onto the \(xy\)-plane.
- \(\phi ,\) \(0\leq \phi \leq \pi \), is the angle between the positive \(z\) -axis and the line segment \({\it OP}\).
The ordered triple \(( \rho ,\theta ,\phi ) \) is called the spherical coordinates of the point \(P.\) See Figure 57(a).
The algebraic relationship between the spherical coordinates \((\rho ,\theta ,\phi )\) of a point \(P\) and the rectangular coordinates \((x,y,z)\) of the point \(P\) is found using the congruent triangles \({\it OQP}\) and \({\it OP}_{1}P\) as shown in Figure 57(b).
Since \[ x=r\cos \theta \quad y=r\sin \theta \quad r=\rho \sin \phi \quad z=\rho \cos \phi \]
it follows that \[\bbox[5px, border:1px solid black, #F9F7ED]{ x=\rho \sin \phi \cos \theta \qquad y=\rho \sin \phi \sin \theta \qquad z=\rho \cos \phi }\tag{1} \]
These equations are used to convert spherical coordinates \(( \rho ,\theta ,\phi ) \) to rectangular coordinates \((x,y,z) \).
Using the distance formula and the equations (1), we obtain \[\bbox[5px, border:1px solid black, #F9F7ED]{ \rho =\sqrt{x^{2}+y^{2}+z^{2}}\qquad \tan \theta =\dfrac{y}{x}\qquad \cos \phi =\dfrac{z}{\rho } \qquad x\neq 0 }\tag{2} \]
These equations are used to convert rectangular coordinates to spherical coordinates.
957
Converting Spherical Coordinates
If the spherical coordinates of a point \(P\) are \(\left( 4,\dfrac{\pi }{6}, \dfrac{2\pi }{3}\right) \), find the rectangular coordinates of \(P\).
Solution We use the equations (1) to convert spherical coordinates to rectangular coordinates. Then \begin{eqnarray*} x& =&\rho \sin \phi \cos \theta =4\sin \dfrac{2\pi }{3}\cos \dfrac{\pi }{6} =4\!\left( \dfrac{\sqrt{3}}{2}\right) \left( \dfrac{\sqrt{3}}{2}\right) =3 \qquad\!\! {\color {#0066A7}{\hbox{\(\rho =4; \theta =\dfrac{\pi}{6}, \phi =\dfrac{2\pi }{3}\)}}}\\ y& =&\rho \sin \phi \sin \theta =4\sin \dfrac{2\pi }{3}\sin \dfrac{\pi }{6} =4\!\left( \dfrac{\sqrt{3}}{2}\right) \left( \dfrac{1}{2}\right) =\sqrt{3} \\[4pt] z& =&\rho \cos \phi =4\cos \dfrac{2\pi }{3}=4\!\left( -\dfrac{1}{2}\right) =-2 \end{eqnarray*}
The rectangular coordinates of \(P\) are \(( 3,\sqrt{3},-2) \).
NOW WORK
Problem 7.
Converting Rectangular Coordinates to Spherical Coordinates
If the rectangular coordinates of a point \(P\) are \(( 1,\sqrt{3} ,-2) \), find the spherical coordinates of \(P\).
Solution We use the equations (2) to convert rectangular coordinates to spherical coordinates. Then \begin{eqnarray*} \rho &=&\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{1+3+4}=\sqrt{8}=2\sqrt{2} \\ \tan \theta &=&\dfrac{y}{x}=\dfrac{\sqrt{3}}{1}, \hbox{ so }\theta =\tan ^{-1}\sqrt{3}=\dfrac{\pi }{3}\qquad \\ \cos \phi &=&\dfrac{z}{\rho }=\dfrac{-2}{2\sqrt{2}}=-\dfrac{\sqrt{2}}{2}, \hbox{ so }\phi =\cos ^{-1}\!\left( -\dfrac{\sqrt{2}}{2}\right) =\dfrac{ 3\pi }{4} \end{eqnarray*}
The spherical coordinates of \(P\) are \(\!\left( 2\sqrt{2},\dfrac{\pi }{3},\dfrac{3\pi }{4}\right) \).
NOW WORK
Problem 9.
NOTE
Points \((\rho ,\theta ,\phi )\) are called spherical coordinates because the surface formed when \(\rho =a\), where \(a\gt 0\) is a constant, is a sphere.
Spherical coordinates are useful in problems involving spheres, vertical planes, and cones because their spherical coordinate equations are relatively simple. See Table 2.
| Surface | Equation in spherical coordinates |
|---|---|
| Sphere | \(\rho =a\quad\) \(a \gt 0\) |
| Half-cone | \(\phi =a\quad\) \(0 \lt a \lt \pi\), \(a\neq \dfrac{\pi}{2}\) |
| Half-plane | \(\theta =a\quad\) \(-\dfrac{\pi}{2} \lt a \lt \dfrac{\pi}{2}\) |
These surfaces are illustrated in Figure 58 on page 958. The half-cone defined by \( \phi =a\), where \(0 \lt a \lt \pi \) and \(a\neq \dfrac{\pi }{2}\), is generated by revolving a ray with its initial point at the origin and forming an angle \(a\) about the \(z\)-axis.
958
2 Find a Triple Integral Using Spherical Coordinates
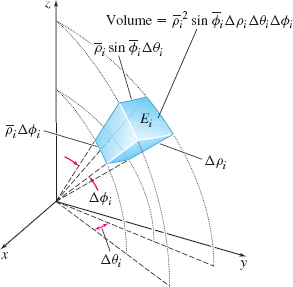
Let \((\rho ,\theta ,\phi )\) be the spherical coordinates of a point, and let \(E\) be a solid in space. Partition \(E\) into wedges by drawing concentric spheres centered at the origin, vertical planes through the \(z\)-axis, and circular cones with their vertex at the origin and axis along the \(z\)-axis. Discard any wedge that does not lie entirely in \(E\). Let \(n\) denote the number of wedges that lie entirely in \(E\). The norm \(\left\Vert P\right\Vert\) of the partition is the length of the longest diagonal of the \(n\) wedges.
We calculate the volume \(\Delta V_{i}\) of a typical wedge \(E_{i}\) by treating it as if it were a rectangular parallelepiped, as shown in Figure 59. Then there is a point \((\bar{\rho}_{i},\bar{\theta} _{i},\overline{\phi}_{i})\) in \(E_{i}\) for which \[ \Delta V_{i}=lwh= (\bar{\rho}_{i}\sin\overline{\phi}_{i}\Delta\theta_i) (\Delta\rho_i) (\bar{\rho}_{i}\Delta\phi_i) = \bar{\rho}_{i}^{2}\sin \overline{\phi } _{i}\,\Delta \rho _{i}\,\Delta \theta _{i}\,\Delta \phi _{i} \]
We evaluate the function \(f\) at the point \((\bar{\rho}_{i},\bar{\theta} _{i},\overline{\phi }_{i})\) in each \(E_{i}\), obtaining \(f(\bar{ \rho}_{i},\bar{\theta}_{i},\overline{\phi }_{i})\). Then we form the sums \[ \begin{equation*} \sum_{i=1}^{n}f( \bar{\rho}_{i},\bar{\theta}_{i},\overline{\phi} _{i}) \,\bar{\rho}_{i}^{2}\sin \overline{\phi }_{i}\,\Delta \rho _{i}\,\Delta \theta _{i}\,\Delta \phi _{i} \end{equation*} \]
It can be shown that if \(f\) is continuous on \(E\), then the limit of the above sums, as the norm \(\left\Vert P\right\Vert\) approaches \(0\), exists. We define the triple integral of \(f\) over \(E\) as this limit. \[\bbox[5px, border:1px solid black, #F9F7ED]{ \iiint\limits_{\kern-3ptE}f(\rho ,\theta ,\phi )\,{\it dV}=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{i=1}^{n}f(\bar{\rho}_{i},\bar{\theta}_{i}, \overline{\phi }_{i})\bar{\rho}_{i}^{2}\sin \overline{\phi }_{i}\,\Delta \rho _{i}\,\Delta \theta _{i}\,\Delta \phi _{i}=\iiint\limits_{\kern-3ptE}f(\rho ,\theta ,\phi )\,\rho ^{2}\,\sin \phi \,d\rho \,d\theta \,d\phi } \]
NOTE
Notice that the integrand contains the factor \(\rho ^{2}\sin \phi\) because in spherical coordinates the differential \({\it dV}\) of the volume \(V\) is \({\it dV}=\rho^{2}\sin \phi \,d\rho \,d\theta \,d\phi\).
Finding a Triple Integral Using Spherical Coordinates
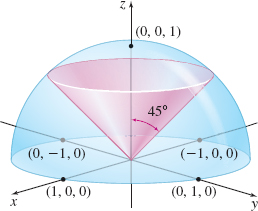
Use spherical coordinates to find the integral \[ \begin{equation*} \iiint\limits_{E}z\,{dx}\,{dy}\,{dz} \end{equation*} \]
where \(E\) is the solid defined by the inequalities \[ 0\leq \sqrt{x^{2}+y^{2}}\leq z\qquad 0\leq x^{2}+y^{2}+z^{2}\leq 1 \]
Solution We convert the rectangular coordinates to spherical coordinates to obtain \(E\) in spherical coordinates. Since \(\rho = \sqrt{ x^{2}+y^{2}+z^{2}}\) and \(x^{2}+y^{2}+z^{2}\leq 1,\) we have \(0\leq \rho \leq 1 \). This is the upper half of a spherical solid of radius 1. Next, the surface \(z= \sqrt{x^{2}+y^{2}}\) (which is a half-cone) can be written \( x^{2}+y^{2}=z^{2}\). The cross section of this cone with the \(xz\)-plane is the pair of lines \(z^{2}=x^{2}\) or \(z=\pm x\), each forming an angle \(\phi = \dfrac{\pi }{4}\) with the positive \(z\)-axis. See Figure 60.
959
Since \(z=\rho \cos \phi\), the integral becomes \[ \begin{eqnarray*} \iiint\limits_{\kern-3ptE}z\,{dx}\,{dy}\,{dz}&=&\iiint\limits_{\kern-3ptE}\rho \cos \phi \cdot\rho ^{2}\sin \phi \,d\rho \,d\phi \,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{\pi/4}\int_{0}^{1}\rho ^{3}\sin \phi \cos \phi \,d\rho \,d\phi \,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{\pi /4}\left[ \int_{0}^{1}\rho ^{3}d\rho \right] \sin \phi \cos \phi \,d\phi \,d\theta =\int_{0}^{2\pi }\int_{0}^{\pi /4}\dfrac{1}{4}\sin \phi \cos \phi \,d\phi \,d\theta\\ &=&\dfrac{1}{4}\int_{0}^{2\pi }\left[ \int_{0}^{\pi /4}\sin \phi \cos \phi\,d\phi \right] d\theta \underset{\underset{\underset{\color{#0066A7}{\hbox{when \(\phi =0,u=1\), when \(\phi =\dfrac{\pi }{4}\), \(u=\dfrac{\sqrt{2}}{2}\)}}}{\color{#0066A7}{\hbox{\(u=\cos \phi, du=-\sin \phi \,d\phi\)}}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{1}{4}\int_{0}^{2\pi }\left[ \int_{1}^{\sqrt{2}/2}-u\,{\it du}\right] d\theta \\ &=&\dfrac{1}{4}\int_{0}^{2\pi }\left[ -\dfrac{u^{2}}{2}\right] _{1}^{\sqrt{2}/2}d\theta =\dfrac{1}{4}\int_{0}^{2\pi }\left( -\dfrac{1}{4}+\dfrac{1}{2}\right) d\theta =\dfrac{1}{16}\int_{0}^{2\pi}\,d\theta =\dfrac{\pi}{8} \end{eqnarray*} \]
NOW WORK
Problems 21 and 25.
Finding the Volume of a Solid Using Spherical Coordinates
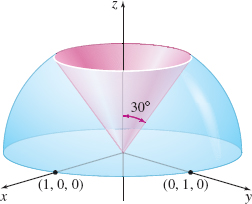
Find the volume of the solid that is removed from a hemisphere of radius 1 when it is cut by a cone that makes an angle of \(30^{\circ}\) with the positive \(z\)-axis.
Solution Figure 61 shows the part of the hemisphere cut by the cone, namely, the volume under the sphere and inside the cone. The upper surface is the hemisphere of radius \(r=1\); the lower surface is the \(xy\)-plane \((z=0)\). The angle \(\theta\) ranges from \(0\) to \(2\pi\) and \(\phi\) ranges from \(0\) to \(\dfrac{\pi}{6}.\) \[ 0\leq \rho \leq 1\qquad 0\leq \theta \leq 2\pi \qquad 0\leq \phi \leq \dfrac{\pi }{6} \]
Then the volume \(V\) of the solid is \[ \begin{eqnarray*} V &=&\iiint\limits_{E}\,\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi =\int_{0}^{\pi /6}\int_{0}^{2\pi}\int_{0}^{1}\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi\\ &=&\int_{0}^{\pi /6}\int_{0}^{2\pi}\left[\int_{0}^{1}\rho ^{2}d\rho \right] \sin\, \phi\, d\theta \,d\phi \notag \\ &=&\int_{0}^{\pi /6}\int_{0}^{2\pi }\left[ \dfrac{\rho ^{3}}{3}\right] _{0}^{1}\,d\theta \sin \phi \,d\phi =\int_{0}^{\pi /6}\left[\int_{0}^{2\pi } \dfrac{1}{3}d\theta \right] \sin \phi \,d\phi \notag \\ &=&\dfrac{2\pi}{3}\int_{0}^{\pi /6}\sin \phi \,d\phi =\left. \dfrac{2\pi }{3 }(-\cos \phi) \right] _{0}^{\pi /6}=\dfrac{2\pi }{3}\left( 1- \dfrac{\sqrt{3}}{2}\right) \end{eqnarray*} \]
NOW WORK
Problem 33.
NOTE
Since \(\rho\) is used as a spherical coordinate, we use \(\delta\) to represent the mass density.
Finding the Mass of a Sphere
Find the mass \(M\) of a sphere if its mass density \(\delta\) is proportional to the distance from the center of the sphere.
Solution Let \(a\) be the radius of the sphere, and position the sphere so that its center is at the origin. In spherical coordinates, the equation of the sphere is \(\rho =a\). The mass density \(\delta\) of the sphere is \(\delta =k\rho,\) where \(k\) is the constant of proportionality. The mass \(M\) is \[ \begin{eqnarray*} M &=&\iiint\limits_{E}\delta \,{dV}=\iiint\limits_{E}k\rho \rho ^{2}\sin \phi \,d\rho \,d\phi \,d\theta =k\iiint\limits_{E}\rho ^{3}\sin \phi \,d\rho \,d\phi \,d\theta\\ &=&k\int_{0}^{2\pi }\int_{0}^{\pi }\left[ \int_{0}^{a}\rho ^{3}\,d\rho \right] \sin \phi \,d\phi \,d\theta \notag \\ & =&k\int_{0}^{2\pi}\int_{0}^{\pi }\left[ \dfrac{\rho ^{4}}{4}\right] _{0}^{a}\,\sin \phi \,d\phi \,d\theta =\dfrac{ka^{4}}{4}\int_{0}^{2\pi }\left[ \int_{0}^{\pi }\sin \phi \,d\phi \right] d\theta\\ &=&\dfrac{ka^{4}}{4} \int_{0}^{2\pi }\big[ -\cos \phi \big] _{0}^{\pi }\,d\theta \notag \\ & =&\dfrac{ka^{4}}{2}\int_{0}^{2\pi }\,d\theta =k\pi a^{4} \end{eqnarray*} \]
960
NOW WORK
Problem 37.
Spherical Coordinates in Navigation
If we assume that the surface of Earth is spherical, there is a simple relationship between the spherical coordinates we have defined and the system of latitude and longitude measurements used in geography.
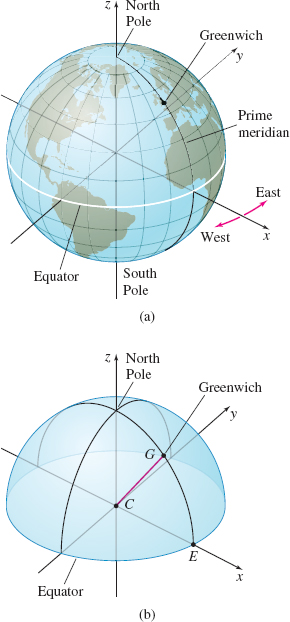
The origin is placed at the center of Earth and the \(z\)-axis is chosen to be the diameter through the North and South Poles. See Figure 62(a). The equator is then the great circle in the \(xy\)-plane. The \(x\)-axis is chosen so that the \(xz\)-plane passes through the Greenwich Observatory near London.
The longitude for a point \(P\) on the surface of Earth is then the angle we have called \(\theta\), except that degree measure is used and east and west are measured from the great circle through the poles and Greenwich. Greenwich has longitude \(0^\circ\).
The latitude for a point on the surface of Earth north of the equator is \(90^\circ -\) \(\phi\); latitude is measured from the equator rather than from the North Pole. For a point on Earth south of the equator, the latitude is \(\phi -90^\circ \). Points on the equator have \(\phi =90^\circ \) and latitude \(0^\circ \). For the North Pole, we write \(\phi =0^\circ \) and north latitude \(90^\circ \); for the South Pole, we write \(\phi =180^\circ \) and south latitude \(90^\circ \).
Finding Longitude and Latitude in Spherical Coordinates
Greenwich, England, has a longitude of \(0^\circ \) and an approximate latitude of \(51.5^\circ \) N. If \(R_{E}=3960\) miles is used for the radius of the Earth and degrees are used to measure angles instead of radians, then the spherical coordinates for Greenwich, England, are \((3960,0^{\circ},38.5^\circ )\). See Figure 62(b), where the angle \(ECG=51.5^\circ \).