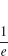Chapter 4Printed Page AN-19
1. 10 m3/min
2. 0.5 m/min
3. 
4. −1
5. 5π2
7. 40
9. 900 cm3/s
11. −0.000625 cm/h
13. 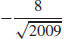 ≈ −0.178 cm/min
≈ −0.178 cm/min
15.  ≈ 0.242 cm2/min
≈ 0.242 cm2/min
17. −0.75 m2/min
19. 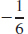 rad/s
rad/s
21. 0.2 m/min
23. 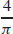 ≈ 1.273 m/min
≈ 1.273 m/min
25. (a) 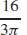 ≈ 1.698 m/min
≈ 1.698 m/min
(b) 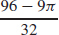 ≈ 2.116 m3/min
≈ 2.116 m3/min
27.  ≈ 4.366 units/s
≈ 4.366 units/s
29. 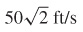
31. 1.75 kg/cm2/min
33. 100.8π ≈ 316.673 ft2/min
35. (a) 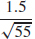 ≈ 0.202 m/s
≈ 0.202 m/s
(b) 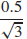 ≈ 0.289 m/s
≈ 0.289 m/s
(c) 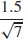 ≈ 0.567 m/s
≈ 0.567 m/s
37. 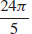 ≈ 15.08 km/s
≈ 15.08 km/s
39. 4 m/min
41. He is rising at  ≈ 68.017 ft/min. He is moving horizontally at −
≈ 68.017 ft/min. He is moving horizontally at −  ≈ − 32.270 ft/min.
≈ − 32.270 ft/min.
43. 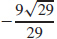 ≈−1.671 m/s
≈−1.671 m/s
45. (a) $150/day
(b) $200/day
(c) $50/day
47. ≈−4.864 lb/s
49. −100π ≈ −314.159 ft/s
51. −316.8 rad/h
53. (a) Answers will vary.
(b) Answers will vary.
55. ≈ 32.071 ft/s
57. ≈ 0.165 in2/min
1. False
2. (b)
3. False
4. False
5. False
6. False
7. x1: neither, x2: local maximum, x3: local minimum and absolute minimum, x4: neither, x5: local maximum, x6: neither, x7: local minimum, x8: absolute maximum
9. 
11. 
13. 4
15. 0, 2
17. −1, 0, 1
19. 0
21. 0
23. π
25. 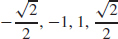
27. 0, 2
29. −3, 0, 1
31. 3, 4
33. 
35. 1
37. Absolute maximum 20 at x = 10, absolute minimum −16 at x = 4
39. Absolute maximum 16 at x = 4, absolute minimum −4 at x = 2
41. Absolute maximum 9 at x = 2, absolute minimum 0 at x = 1
43. Absolute maximum 1 at x = −1, 1, absolute minimum 0 at x = 0
45. Absolute maximum 4 at x = 4, absolute minimum 2 at x = 1
47. Absolute maximum π at x = π, absolute minimum 0 at x = 0
49. 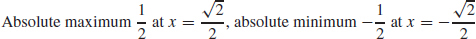
51. Absolute maximum 0 at x = 0, absolute minimum 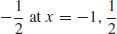
53. Absolute maximum 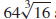 at x = 5, absolute minimum 0 at x = −3, 1
at x = 5, absolute minimum 0 at x = −3, 1
55. Absolute maximum  at x = 4, absolute minimum −1 at x = 2
at x = 4, absolute minimum −1 at x = 2
57. Absolute maximum 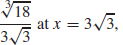 , absolute minimum 0 at x = 3
, absolute minimum 0 at x = 3
59. Absolute maximum 1 at x = 0, absolute minimum e − 3 at x = 1
61. Absolute maximum 9 at x = 3, absolute minimum 1 at x = 0
63. Absolute maximum 8 at x = 2, absolute minimum 0 at x = 0
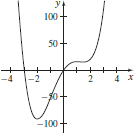
65. (a) f′(x) = 12x3 − 6x2 − 42x + 36
(b) −2, 1,
(c) Absolute minimum at x = −2, local maximum at x = 1, local minimum at x = 
67. (a) f′(x) = 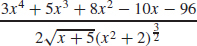
(b) −5, ≈−2.364, ≈1.977
(c) Local maximum at x ≈ −2.364,
local minimum at x ≈ 1.977,
neither a local minimum nor a local maximum at x = −5. 
69. (a) f′(x) = 4x3 − 37.2x2 + 98.48x − 68.64
(b) Absolute maximum 0 at x = 0, absolute minimum −37.2 at x = 5
(c)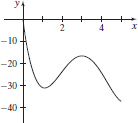
71. (a) 50 mi/h
(b)
73. (a) 67.5°, 0.0183v02 ft
(b) 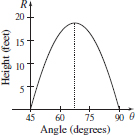
(c) Answers will vary.
75. (a) See Student Solutions Manual.
(b) ≈846.858 m
77. 
79. 5 m
81. (a) 0.04, 0.07
(b) Absolute maximum −3.719 at x = 1, absolute minimum −4.391 at x = −1
(c)
83. Absolute maximum 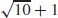 at x = 3, absolute minimum
at x = 3, absolute minimum 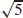 at x = 2
at x = 2
85. (a) [−4,−3]  [3, 4]
[3, 4]
(b) 
87. (c) (e)
89. See Student Solutions Manual.
91. See Student Solutions Manual.
93. (a) See Student Solutions Manual.
(b) Answers will vary.
1. False
2. Answers will vary.
3. True
4. False
5. 
7. 1
9. 
11. 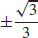
13. ±1, 0
15. 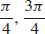
17. f (−2) ≠ f (1)
19. f is not differentiable at x = 0.
21. 1
23. e – 1
25. 
27. 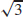
29. 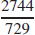
31. f is increasing on (−∞,∞).
33. f is increasing on [−1, 0]  [1,∞) and decreasing on (−∞,−1]
[1,∞) and decreasing on (−∞,−1]  [0, 1].
[0, 1].
35. f is increasing on [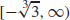 and decreasing on
and decreasing on  ].
].
37. f is increasing on 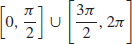 and decreasing on
and decreasing on 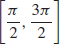 .
.
39. f is increasing on [−1,∞) and decreasing on (−∞,−1].
41. f is increasing on 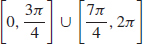 and decreasing on
and decreasing on 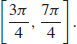
43. See Student Solutions Manual.
45. See Student Solutions Manual.
47. Answers will vary.
49. See Student Solutions Manual.
51. See Student Solutions Manual.
53. (a) See Student Solutions Manual.
(b) d(0) = d(5) = 0
(c) ≈2.892 ft; d(2.892) ≈ −0.423 ft.
(d)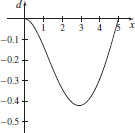
55. See Student Solutions Manual.
57. See Student Solutions Manual.
59. Answers will vary.
61. 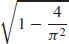
63. (a) 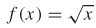 is increasing on the interval (0, 0).
is increasing on the interval (0, 0).
(b) Yes.
65. (b)
67. See Student Solutions Manual.
69. See Student Solutions Manual.
71. See Student Solutions Manual.
73. See Student Solutions Manual.
75. For b2 −3ac ≤ 0, f is increasing on (−∞,∞) for a = 0 and decreasing on (−∞,∞) for a < 0. For b2 −3ac = 0 and a = 0, f is increasing on (−∞, x1]  [x2,∞) and decreasing on [x1, x2]. For b2 −3ac > 0 and a < 0, f is increasing on [x1, x2] and decreasing on (−∞, x1]
[x2,∞) and decreasing on [x1, x2]. For b2 −3ac > 0 and a < 0, f is increasing on [x1, x2] and decreasing on (−∞, x1]  [x2,∞),
[x2,∞),  .
.
77. See Student Solutions Manual.
79. See Student Solutions Manual.
81. 0 is the only critical number. If n is odd and ad − bc > 0, then f is increasing on the domain. If n is odd and ad −bc < 0, then f is decreasing on the domain. If n is even and ad −bc > 0, then f is increasing on the domain where x = 0 and decreasing on the domain where x < 0. If n is even and ad − bc < 0, then f is increasing on the domain where x < 0 and decreasing on the domain where x > 0.
83. See Student Solutions Manual.
1. False
2. False
3. (a)
4. (b)
5. (a)
6. (c)
7. True
8. False
9. (a) Local maximum at (−1, 0), local minimum at (−2.5,−4) and (0.5,−4), inflection points (−1.8,−2) and (−0.2,−2)
(b) Increasing on [−2.5,−1]  [0.5,∞), decreasing on (−∞,−2.5]
[0.5,∞), decreasing on (−∞,−2.5]  [−1, 0.5], concave up on (−∞,−1.8)
[−1, 0.5], concave up on (−∞,−1.8)  (−0.2,∞), concave down on (−1.8,−0.2)
(−0.2,∞), concave down on (−1.8,−0.2)
11. (a) Local maximum at (−2, 3) and (12, 10), local minimum at (0, 0), no inflection point
(b) Increasing on (−∞,−2]  [0, 12], decreasing on [−2, 0]
[0, 12], decreasing on [−2, 0]  [12,∞), never concave up, concave down on (−∞, 0)
[12,∞), never concave up, concave down on (−∞, 0)  (0,∞)
(0,∞)
13. (a) 0, 4
(b) Local maximum 2 at 0, local minimum −30 at 4
15. (a) 0, 1
(b) Local minimum −1 at 1
17. (a)
(b) Local maximum 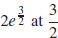
19. (a) 1
(b) Local minimum e at 1
21. (a) 
(b) Local minimum 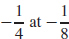
23. (a) −1, 0, 1
(b) Local maximum 0 at 0, local minimum −3 at −1 and 1
25. (a)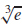
(b) Local maximum 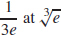
27. (a) −1, 0, 1
(b) Local maximum 1 at 0, local minimum 0 at −1 and 1
29. (a) kπ – tan−1 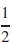 , k an integer
, k an integer
(b) Local maximum  local minimum
local minimum 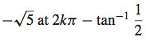
31. (a) The object moves right on (1,∞), left on (0, 1)
(b) t = 1
(c) The velocity is increasing on (0,∞)
(d) 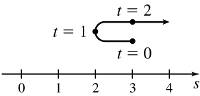
(e) 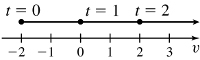
33. (a) The object moves right on (1,∞), left on (0, 1)
(b) t = 1
(c) The velocity is increasing on (0,∞)
(d) 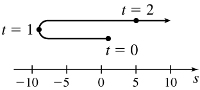
(e) 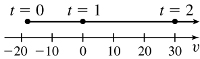
35. (a) The object moves right on (0,∞)
(b) No direction reverse
(c) The velocity is decreasing on (0,∞)
(d) 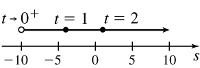
(e) 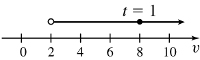
37. (a) The object moves right on 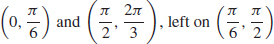
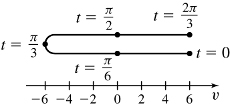
(b) t = 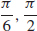
(c) The velocity is 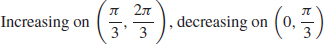
(d)
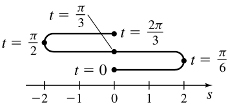
(e)
39. (a) Concave up on (−∞,∞)
(b) No inflection point
41. (a) Concave up on (3,∞), concave down on (−∞, 3)
(b) (3,−52)
43. (a) Concave up on (−∞, 0)  (2,∞), concave down on (0, 2)
(2,∞), concave down on (0, 2)
(b) (0, 10), (2,−6)
45. (a) Concave up on 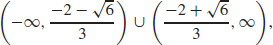 Concave down on
Concave down on 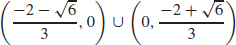
(b) (−1.483, 0.295), (0.150, 0.328)
47. (a) Concave up on (e7/12,∞), concave down on (0, e7/12)
(b) 
49. (a) Concave up on (0,∞), concave down on (−∞, 0)
(b) No inflection point
51. (a) Concave up on (−∞, 0), concave down on (0,∞)
(b) (0, 0)
53. (a) Concave up on (−∞, 0)  (0, 3), concave down on (3,∞)
(0, 3), concave down on (3,∞)
(b) 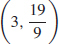
55. (a) No local extrema
(b) Concave up on (1,∞), concave down on (−∞, 1)
(c) (1,−1)
57. (a) Local minimum −3 at x = 1
(b) Concave up on (−∞, 0)  (0,∞)
(0,∞)
(c) No inflection point
59. (a) Local maximum 256 at x = 4, local minimum 0 at x = 0
(b) Concave up on (−∞, 0)  (0, 3), concave down on (3,∞)
(0, 3), concave down on (3,∞)
(c) (3, 162)
61. (a) Local maximum 64 at x = −2, local minimum −64 at x = 2
(b) Concave up on 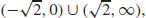 concave down on
concave down on 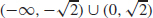
(c) (0, 0), 
63. (a) Local maximum 4e−2 at x = −2, local minimum 0 at x = 0
(b) Concave up on 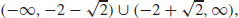 , concave down on
, concave down on 
(c) 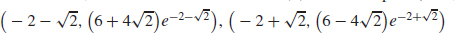
65. (a) Local minimum 1 at x = 0
(b) Concave up on (−∞,∞)
(c) No inflection point
67. (a) Local minimum 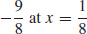
(b) Concave up on 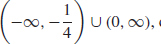 concave down on
concave down on 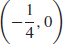
(c) 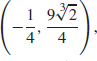 (0, 0)
(0, 0)
69. (a) 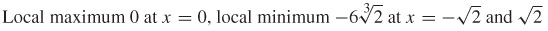
(b) Concave up on (−∞, 0)  (0,∞)
(0,∞)
(c) No inflection point
71. (a) Local minimum 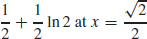
(b) Concave up on (0,∞)
(c) No inflection point
73. (a) Local maximum  local minimum
local minimum 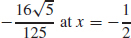
(b) Concave up on 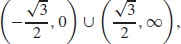 concave down on
concave down on 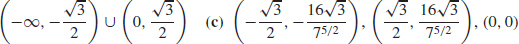
75. (a) Local maximum 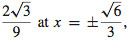 local minimum 0 at x = 0
local minimum 0 at x = 0
(b) Concave up on  concave down on
concave down on 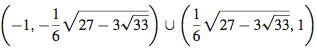
(c)
77. (a) Local maximum 1 at x=kπ+π2, local minimum 0 at x = kπ, k an integer.
(b) Concave up on (kπ−π4,kπ+π4), concave down on (kπ+π4,kπ+3π4), k an integer.
(c) ((2k+1)π4,12), k an integer.
79. (a) Local maximum 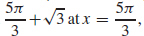 local minimum
local minimum 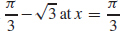
(b) Concave up on (0, π), concave down on (π, 2π)
(c) (π, π)
81. (a) Local maximum −20 at x = 3, local minimum −21 at x = 2
(b) Same as (a)
(c) Answers will vary
83. (a) Local maximum 4e at x = 1, local minimum 0 at x = 3
(b) Same as (a)
(c) Answers will vary.
85. Answers will vary.
87. Answers will vary.
89. Answers will vary.
91. Answers will vary.
93. Answers will vary.
95. Answers will vary.
97. (a) Concave up on 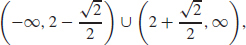 concave down on
concave down on 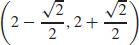
(b) 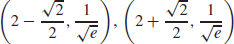
(c) 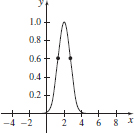
99. (a) Concave up on (−∞, 0.135)  (0.721, 5.144), concave down on (0.135, 0.721)
(0.721, 5.144), concave down on (0.135, 0.721)  (5.144,∞)
(5.144,∞)
(b) (0.135, 2.433), (0.721, 2.139), (5.144, -0.072)
(c) 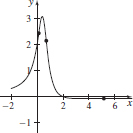
101. See Student Solutions Manual.
103. a = −3, b = 9
105. (a) N′(t) = 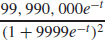
(b) N′(t) is increasing on the interval (0, ln 9999) and decreasing on the interval (ln 9999,∞).
(c) ln 9999
(d) (ln 9999, 5000)
(e) Answers will vary.
107. (a)
(b) Answers will vary.
(c) 
(d) P′(t) is increasing on the interval (0, 133.843) and decreasing on the interval (133.843,∞).
(e) The rate of change in population is maximum when t = 133.843.
(f) (133.843, 381088358.9)
(g) Answers will vary.
109. (a) Local minimum B(2.80) ≈ −328.53 billion dollars, local maximum B(5.71) ≈ −170.80 billion dollars.
(b) Both represent a budget deficit.
(c) Concave up on (0, 4.26), concave down on (4.26, 9), (4.26,−249.27) is a point of inflection.
(d) To the left of the inflection point, the budget is increasing at an increasing rate. To the immediate right of the inflection point, the budget is increasing at a decreasing rate.
(e) 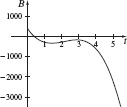
Answers will vary.
111. 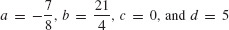
113. Local maximum 2 at 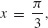 local minimum −2 at
local minimum −2 at 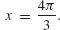 Inflection points
Inflection points 
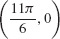
115. f″(x) does not exist at the critical number x = 0.
117. (e)
119. See Student Solutions Manual.
121. See Student Solutions Manual.
123. See Student Solutions Manual.
125. See Student Solutions Manual.
127. See Student Solutions Manual.
129. See Student Solutions Manual.
131. See Student Solutions Manual.
133. See Student Solutions Manual.
135. See Student Solutions Manual.
1. False
2. False
3. False
4. False
5. Answers will vary.
6. Answers will vary.
7. (a) Yes, (b) 
9. (a) No, (b) Answers will vary.
11.(a) Yes, (b) 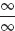
13. (a) No, (b) Answers will vary.
15. (a) Yes, (b) 
17. (a) Yes, (b) 
19. (a) Yes, (b) 0 · ∞
21. (a) Yes, (b) ∞−∞
23. (a) Yes, (b) ∞0
25. (a) No, (b) Answers will vary.
27.  , 5
, 5
29. 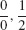
31.  , 2
, 2
33.  , −π
, −π
35. 
37. 
39. 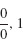
41. 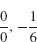
43. 0 · ∞, 0
45. 0 · ∞, 1
47. ∞−∞, 0
49. ∞−∞, −1
51. 00, 1
53. ∞0, 1
55. ∞0, 1
57. 1∞, 1
59. 2
61. 0
63. 0
65. 2
67. 1
69. 
71. 0
73. 0
75. 1
77. 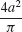
79. 
81. −1
83. 1
85. 1
87. 1
89. 1
91. (a) 366
(b) Answers will vary.
(c)
93. (a)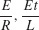
(b) Answers will vary.
95. See Student Solutions Manual.
97. See Student Solutions Manual.
99. 0
101. See Student Solutions Manual.
103. See Student Solutions Manual.
105. (a) See Student Solutions Manual. f′(0) = 0
(b)
107. See Student Solutions Manual.
109. (a) 0
(b) a
(c) ∞
(d) Does not exist.
(e) 0
(f) a
(g) 1
(h) a
(i) Does not exist.
(j) e−1
111. (a) f″(x)
(b) f‴(x)
(c) 
113. See Student Solutions Manual.
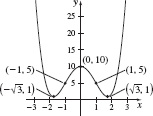
1. 
3. 
5. 
7. 
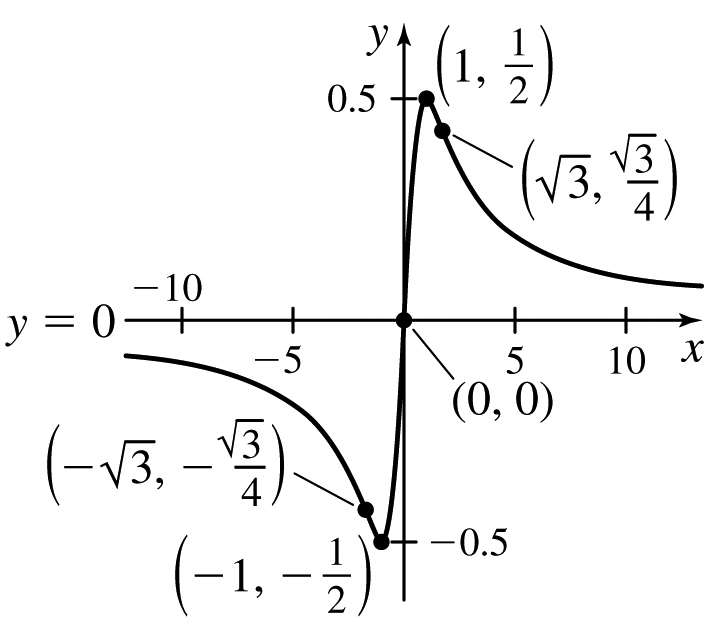
9. 
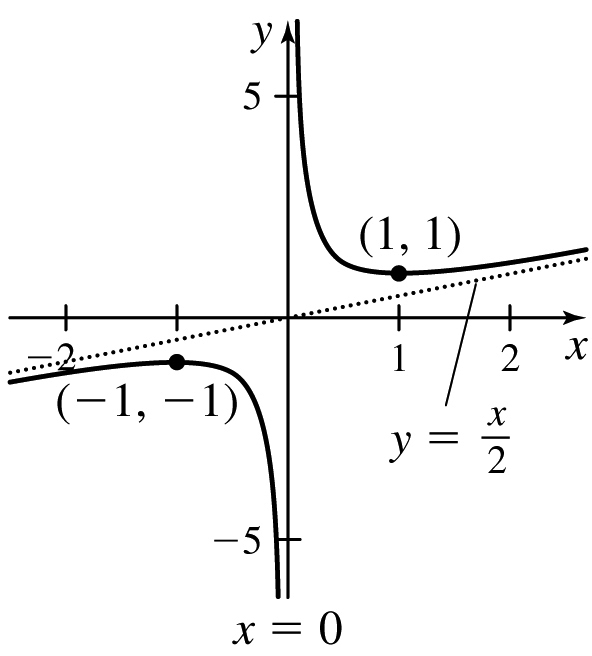
11. 
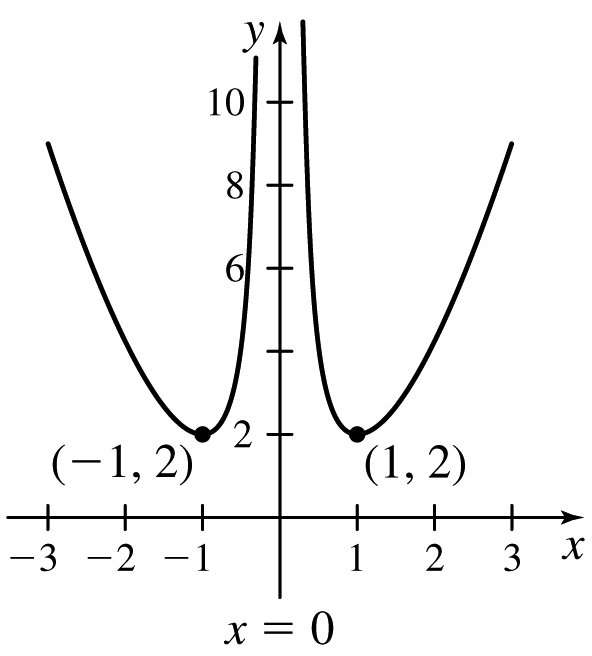
13. 
15. 
17. 
19. 
21. 
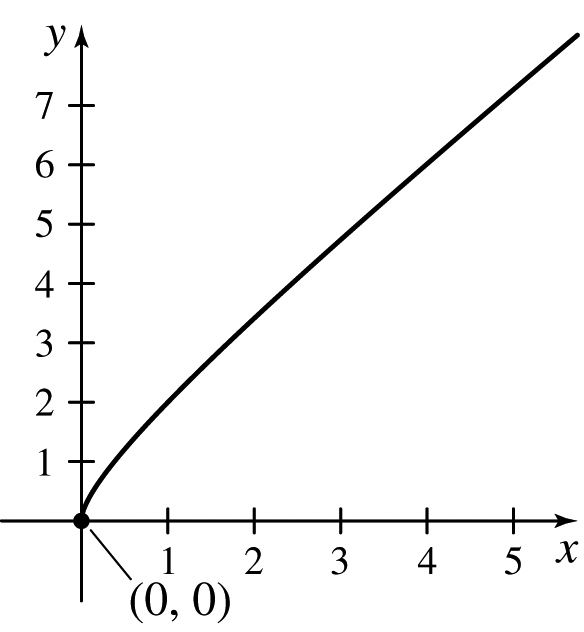
23. 
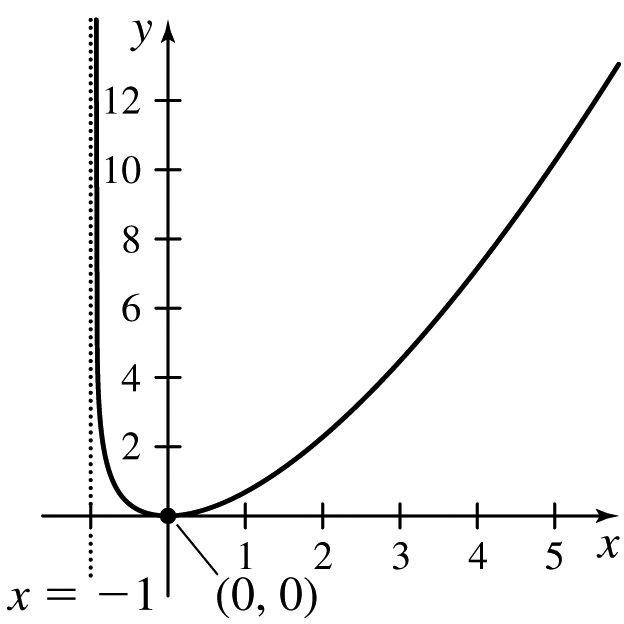
25. 
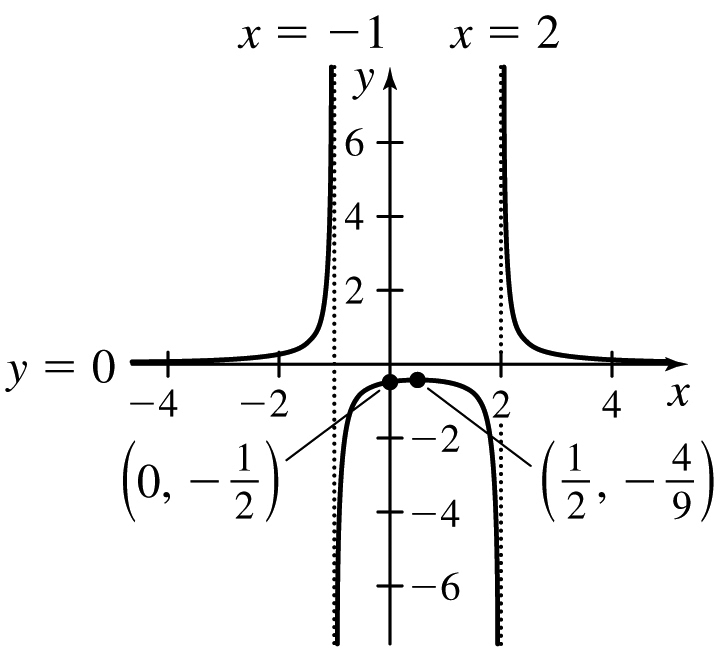
27. 
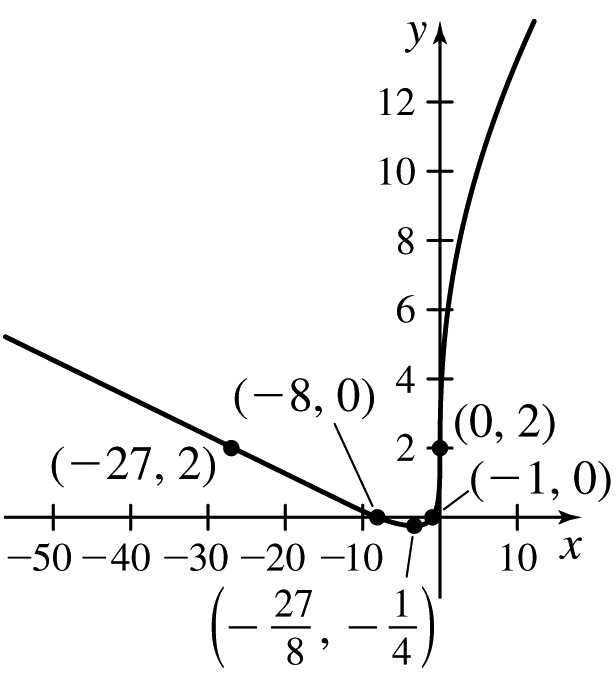
29. 
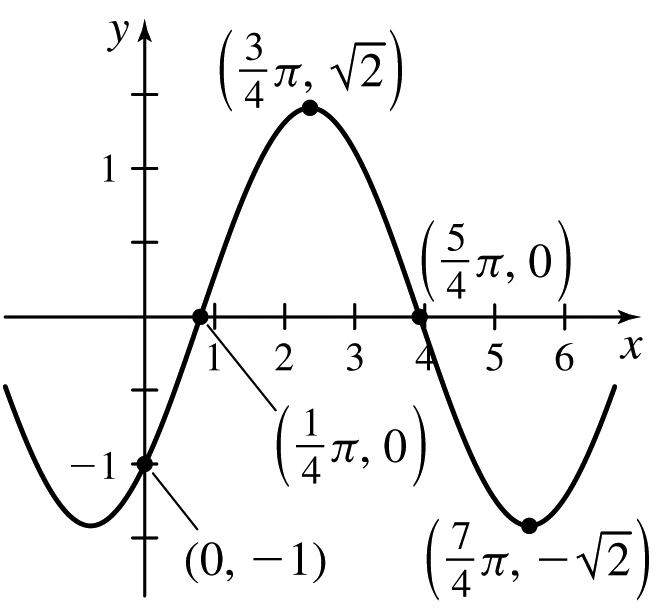
31. 
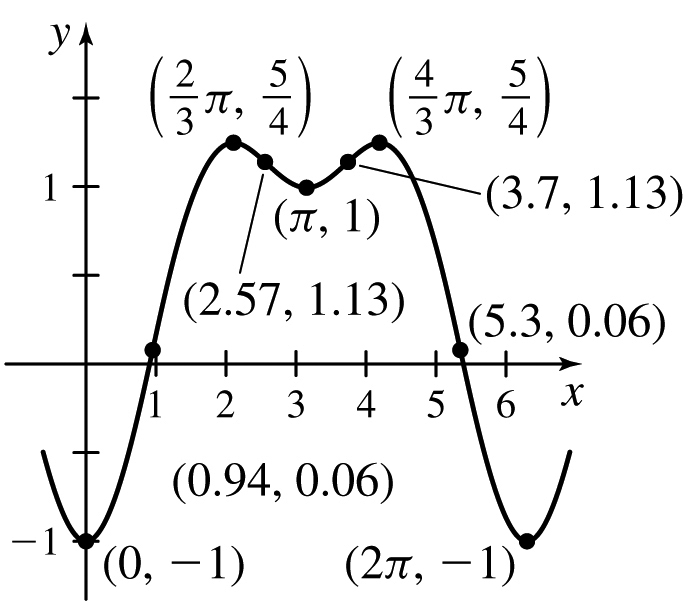
33. 
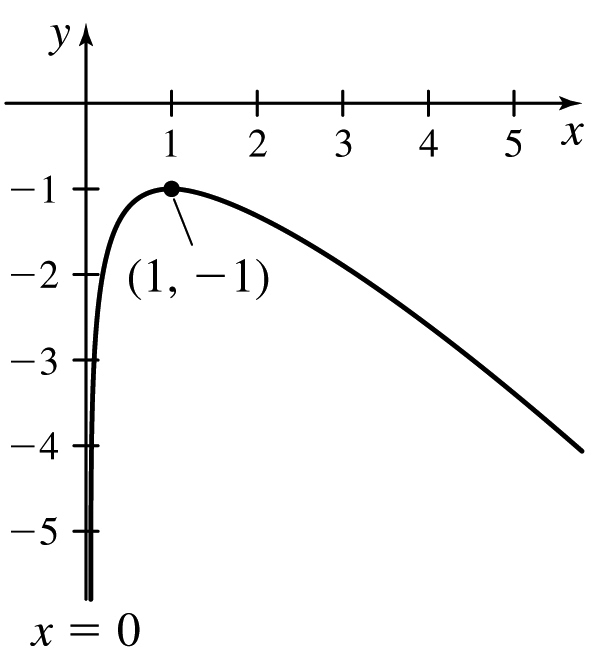
35. 
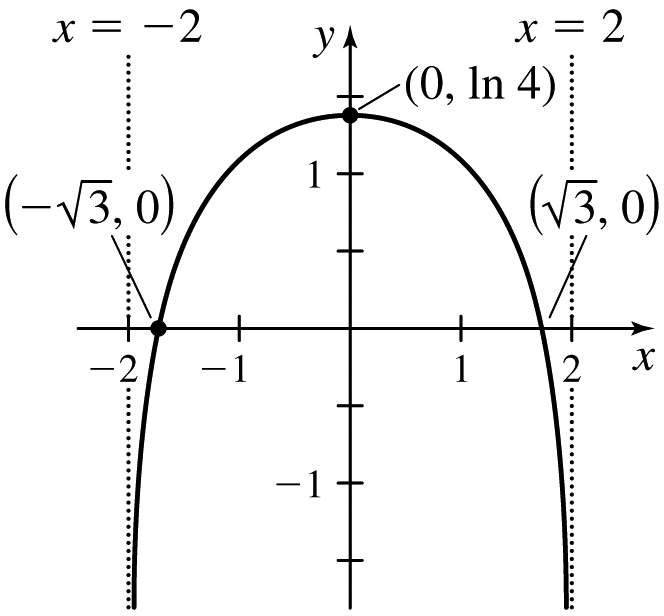
37. 
39. 
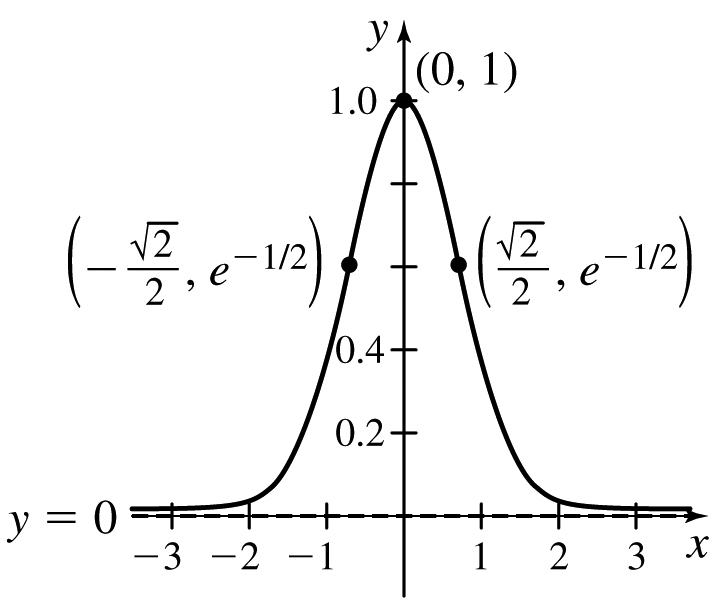
41. 
43. (a) 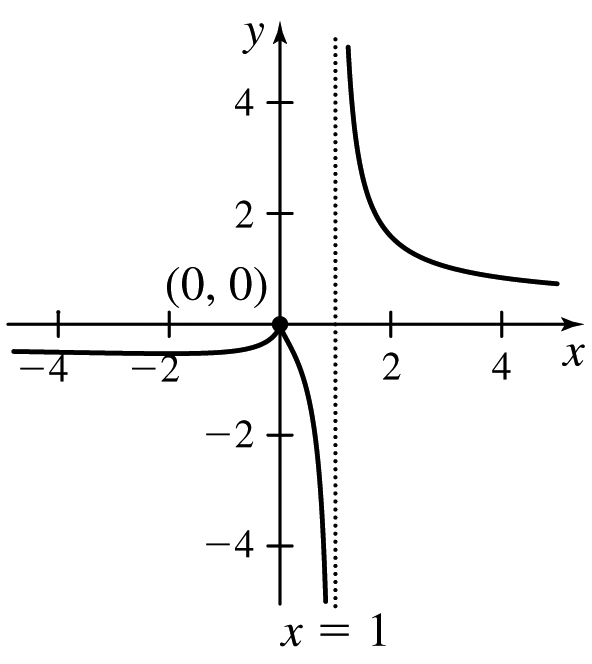
(b) Vertical asymptote: x = 1, horizontal asymptote: y = 0
(c) Decreasing on approximately (−∞,−2)  (0, 1)
(0, 1)  (1,∞) and increasing on approximately (−2, 0), concave down on approximately (−∞,−4)
(1,∞) and increasing on approximately (−2, 0), concave down on approximately (−∞,−4)  (0.1, 1) and concave up on approximately (−4, 0)
(0.1, 1) and concave up on approximately (−4, 0)  (0, 0.1)
(0, 0.1)  (1,∞)
(1,∞)
(d) Local minimum value at approximately −2 and local maximum value at approximately 0
(e) They are the same.
(f) Points of inflection at approximately 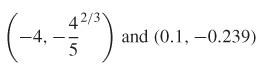
45. (a) 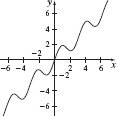
(b) No asymptotes
(c) Increasing on 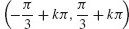 and decreasing on
and decreasing on  for k an integer, f is concave up on
for k an integer, f is concave up on 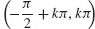 and concave down on
and concave down on  for k an integer.
for k an integer.
(d) Local maximum value at approximately 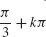 and local maximum value at approximately
and local maximum value at approximately  for k an integer.
for k an integer.
(e) They are the same.
(f) 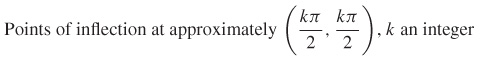 for k an integer.
for k an integer.
47. (a) 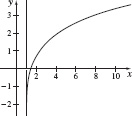
(b) Vertical asymptote: x = 1
(c) Increasing and concave down on approximately (1,∞)
(d) No local extrema
(e) They are the same.
(f) No points of inflection
49. (a) 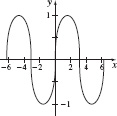
(b) No asymptotes
(c) Increasing approximately on  and decreasing on
and decreasing on 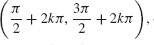 concave up approximately on (−π + 2kπ, 2kπ) and concave down approximately on (2kπ, π + 2kπ) for k an integer.
concave up approximately on (−π + 2kπ, 2kπ) and concave down approximately on (2kπ, π + 2kπ) for k an integer.
(d) Local maximum value at approximately 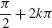 and local minimum value at approximately
and local minimum value at approximately 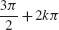 for k an integer.
for k an integer.
(e) They are the same.
(f) Points of inflection at approximately (kπ, 0), k an integer.
51. (a) 
(b) No asymtotes.
(c) Decreasing on (-∞, 0)  (4, 6); Increasing on (0, 4); Concave up on (-∞, 0); Concave down on (0, 6)
(4, 6); Increasing on (0, 4); Concave up on (-∞, 0); Concave down on (0, 6)
(d) Local minimum value of 0 at x = 0, and local maximum value of 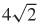 at x = 4.
at x = 4.
(e) They are the same.
(f) There is an inflection point at (0, 0).
53. Answers will vary.
55. Answers will vary.
57. Answers will vary.
59. (a) Absolute maximum value e − 1 at x =  and absolute minimum value 1 at x = 1
and absolute minimum value 1 at x = 1
(b) Concave up on  and concave down on (2, e)
and concave down on (2, e)
(c)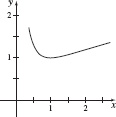
61.  x = ±2 are two vertical asymptotes.
x = ±2 are two vertical asymptotes.
63. 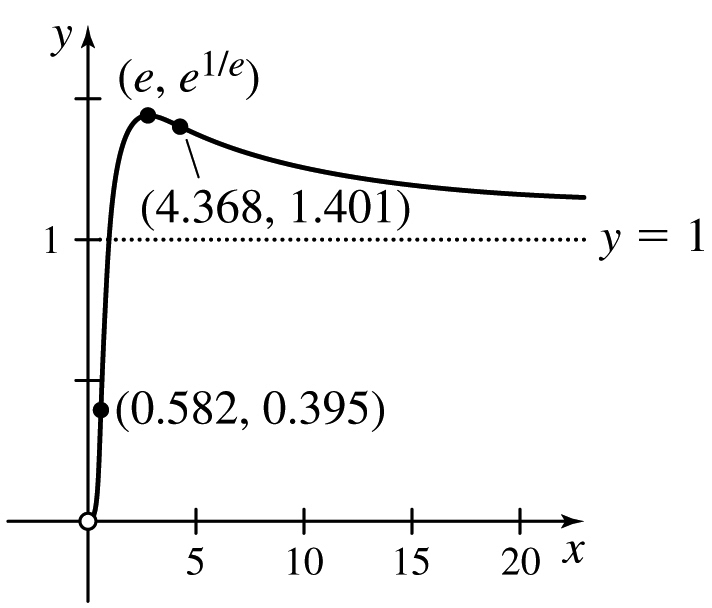 y = 1 is a horizontal asymptote.
y = 1 is a horizontal asymptote.
1. 1,125,000 m2
3. 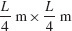
5. 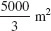
7. 8 cm × 8 cm × 2 cm
9. 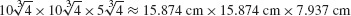
11. Radius 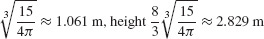
13. $21 per day
15. (1, 1)
17. (1.784, 0.817)
19. (a) 40 mi/h
(b) ≈46.6 mi/h
(c) ≈51.0 mi/h
21. (a) 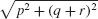
(b) 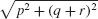
23. ≈9.582 m, ≈36.383o
25. 
27. 594 cases, $456 per case
29. 
31. 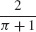
33. 2 m from the weak light source.
35. minimum length: 28.359 cm, maximum length: 42.758 cm
37. (a) Cut 19.603 cm for a square and 15.397 cm for a circle.
(b) Cut 0 cm for a square and 35 cm for a circle.
(c)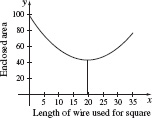
39. See Student Solutions Manual.
41. 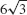
43. 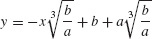
45. See Student Solutions Manual.
47. Observer should stand approximately 4.583 m from the wall.
49. See Student Solutions Manual.
51. 20 ft
53. (−3.758, 6.547)
1. Antiderivative
2. True
3. ln |x| + C
4. True
5. False
6. True
7. True
8. True
9. 2x + C
11. 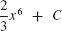
13. 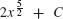
15. 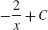
17. 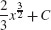
19. x4−x3 +x +C
21. 3x3−6x2 +4x +C
23. 3x −2 ln|x|+C
25. x2 −3 sin x +C
27. 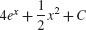
29. 7 tan-1x + C
31. y = x3 − x2 + x – 5
33. 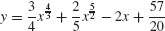
35. 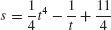
37. 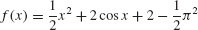
39. y = ex − x + 1
41. s(t) = −16t2 + 128t
43. s(t) = 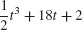 t3 + 18t + 2
t3 + 18t + 2
45. 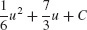
47. 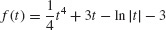
49. F(x) = x cos x + sin x + 1
51. vo = 10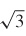 m/s ≈ 38.74 mi/hr
m/s ≈ 38.74 mi/hr
53. 220 ft
55. 15.00625 m
57. 13.133 m/s
59. 8 N
61. ≈16.759 m/s
63. (a) See Student Solutions Manual.
(b) Answers will vary.
(c) I (x) = I0e−kx
(d)
−12ln0.1
1. 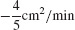
3. 318.953 mph
5. (−8,−9) is an absolute minimum, (−5, 0) is neither, (−2, 9) is a local maximum and an absolute maximum, (1, 0) is a local minimum, (3, 4) is a local maximum, (5, 0) is neither
7. 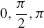
9. Absolute maximum value of 21 at x = −2 and absolute minimum value of −11 at x = 2
11. 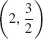
13. (a) Local maximum 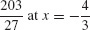 and local minimum −11 at x = 2
and local minimum −11 at x = 2
(b) Same as (a).
15. (a) Local maximum 16e−4 at x = 2 and local minimum 0 at x = 0
(b) Same as (a).
17. 
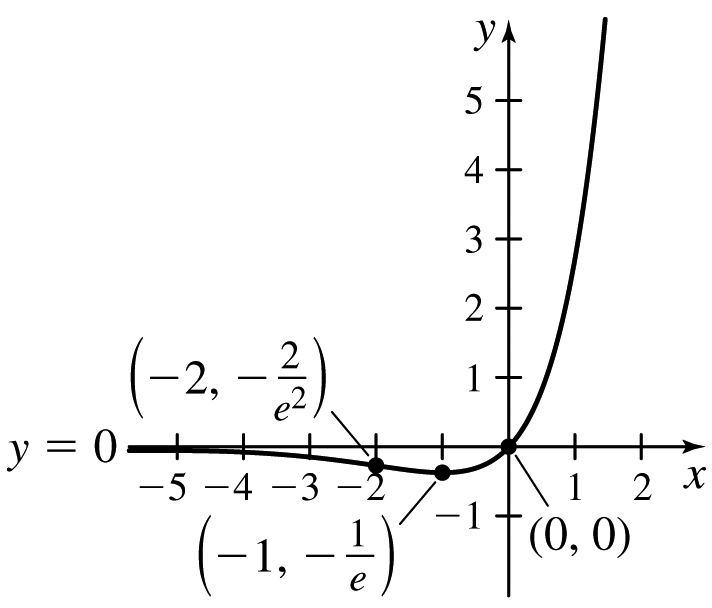
19. 
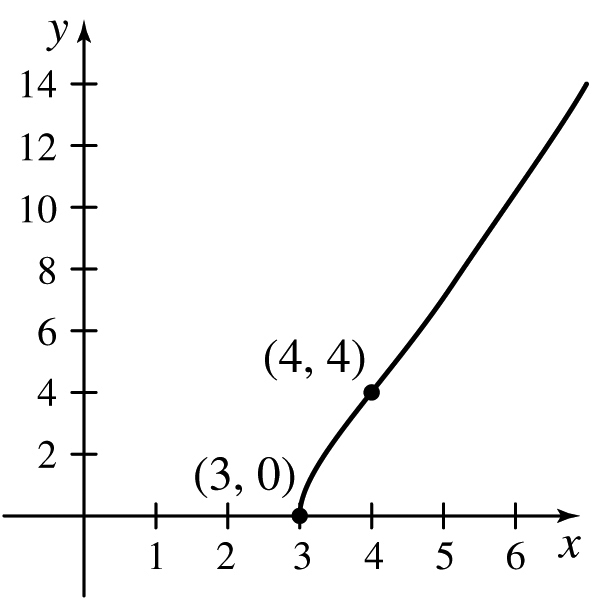
21. 
23. (a) Increasing on (−1.207,∞) and decreasing on (−∞,−1.207)
(b) Concave up on (−∞,∞)
(c) No point of inflection
25. (B)
27. Answers will vary.
29. 10 - 2 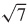 in.
in.
31. F(x) = C
33. F(x) = sin x + C
35. F(x) = 2 ln |x| + C
37. F(x) = x4 − 3x3 + 5x2 − 3x + C
39. 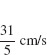
41. Yes, 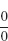
43. Yes,∞−∞
45. 9
47. 2
49. 1
51. 
53. 1
55. 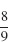
57. y = ex +1
59. y = 2 ln |x| + 4
61. 1075 items
63.