3.6 Hyperbolic FunctionsPrinted Page 243
243
1 Define the Hyperbolic FunctionsPrinted Page 243
Functions involving certain combinations of ex and e−x occur so frequently in applied mathematics that they warrant special study. These functions, called hyperbolic functions, have properties similar to those of trigonometric functions. Because of this, they are named the hyperbolic sine (sinh), the hyperbolic cosine (cosh), the hyperbolic tangent (tanh), the hyperbolic cotangent (coth), the hyperbolic cosecant (csch), and the hyperbolic secant (sech).
DEFINITION
The hyperbolic sine function and hyperbolic cosine function are defined as \bbox[5px, border:1px solid black, #F9F7ED]{y = \sinh x = \dfrac{e^{x}-e^{-x}}{2}\quad y = \cosh x = \dfrac{e^{x} + e^{-x}}{2} }
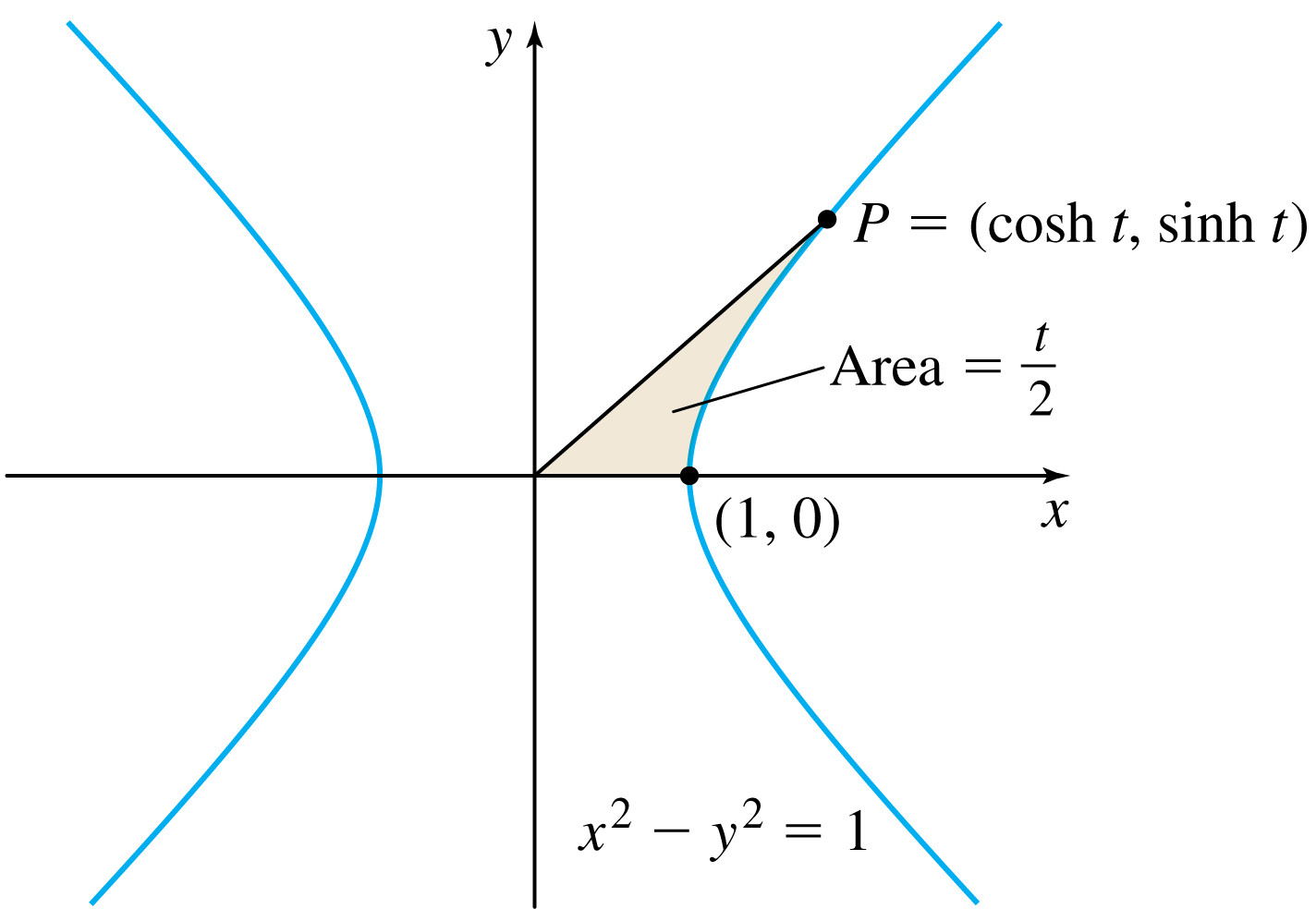
Hyperbolic functions are related to a hyperbola in much the same way as the trigonometric functions (sometimes called circular functions) are related to the circle. Just as any point P on the unit circle x^{2}+y^{2}=1 has coordinates ( \cos t,\sin t), as shown in Figure 20, a point P on the hyperbola x^{2}-y^{2}=1 has coordinates (\cosh t, \sinh t), as shown in Figure 21. Moreover, both the sector of the circle shown in Figure 20 and the shaded portion of Figure 21 have areas that each equal \dfrac{t}{2}.
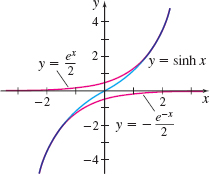
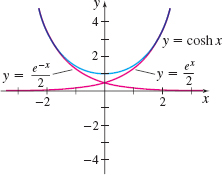
The functions y=\sinh x and y=\cosh x are defined for all real numbers. The hyperbolic sine function, y=\sinh x, is an odd function, so its graph is symmetric with respect to the origin; the hyperbolic cosine function, y=\cosh x, is an even function, so its graph is symmetric with respect to the y-axis. Their graphs may be found by combining the graphs of y=\dfrac{e^{x}}{2} and y=\dfrac{e^{-x}}{2}, as illustrated in Figures 22 and 23, respectively. The range of y=\sinh x is all real numbers, and the range of y=\cosh x is the interval [ 1,\infty ) .
The remaining four hyperbolic functions are combinations of the hyperbolic cosine and hyperbolic sine functions, and their relationships are similar to those of the trigonometric functions.
244
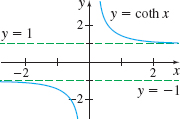
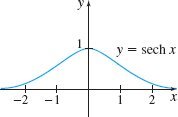
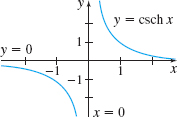
\begin{eqnarray*} \hbox{Hyperbolic tangent:} & y&=&\tanh x=\dfrac{\sinh x}{ \cosh x}=\dfrac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\\[11pt] \hbox{Hyperbolic cotangent:} & y&=&\coth x=\dfrac{\cosh x}{\sinh x} =\dfrac{e^{x}+e^{-x}}{e^{x}-e^{-x}}\\[11pt] \hbox{Hyperbolic secant:} & y&=&\sec\!{\rm h}\,x=\dfrac{1}{ \cosh x}=\dfrac{2}{e^{x}+e^{-x}}\\[11pt] \hbox{Hyperbolic cosecant:} & y&=&\csc\!{\rm h}\,x=\dfrac{1}{\sinh x}=\dfrac{2}{e^{x}-e^{-x}} \end{eqnarray*}
EXAMPLE 1Evaluating Hyperbolic Functions
Find the exact value of:
| (a) \cosh 0 | (b) {\mathop{\rm{sech}}}~0 | (c) \tanh ( \ln 2) |
Solution (a) \cosh 0=\dfrac{e^{0}+e^{0}}{2}=\dfrac{2}{2}=1
(b) {\mathop{\rm{sech}}}~0=\dfrac{1}{\cosh 0}=\dfrac{1}{1}=1
(c) \tanh ( \ln 2) =\dfrac{e^{\ln 2}-e^{-\ln 2}}{e^{\ln 2}+e^{-\ln 2}}=\dfrac{2-e^{\ln ( 1/2) }}{2+e^{\ln ( 1/2) }}=\dfrac{2-\dfrac{1}{2}}{2+\dfrac{1}{2}}=\dfrac{3}{5}
NOW WORK
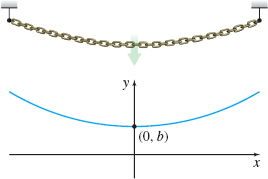
The hyperbolic cosine function has an interesting physical interpretation. If a cable or chain of uniform density is suspended at its ends, such as with high-voltage lines, it will assume the shape of the graph of a hyperbolic cosine.
Suppose we fix our coordinate system, as in Figure 28, so that the cable, which is suspended from endpoints of equal height, lies in the xy-plane, with the lowest point of the cable at the point ( 0,b) . Then the shape of the cable will be modeled by the equation y=a\cosh \dfrac{x}{a}+b-a
where a is a constant that depends on the weight per unit length of the cable and on the tension or horizontal force holding the ends of the cable. The graph of this equation is called a catenary, from the Latin word catena that means “chain.”
2 Establish Identities for Hyperbolic FunctionsPrinted Page 244
There are identities for the hyperbolic functions that remind us of the trigonometric identities. For example, \tanh x=\dfrac{\sinh x}{\cosh x} and \coth x=\dfrac{1}{\tanh x}. Other useful hyperbolic identities include \bbox[5px, border:1px solid black, #F9F7ED] {\cosh ^{2}x-\sinh ^{2}x=1\qquad \tanh^{2}x+\hbox{sech}^{2}x=1\qquad \coth^{2}x-\hbox{csch}^{2}x=1}
245
EXAMPLE 2Establishing Identities for Hyperbolic Functions
Establish the identity \cosh ^{2}x-\sinh ^{2}x=1.
Solution
\begin{eqnarray*} \cosh ^{2}x-\sinh ^{2}x&=&\left( \dfrac{e^{x}+e^{-x}}{2}\right) ^{2}-\left( \dfrac{e^{x}-e^{-x}}{2}\right) ^{2}\\ &=&\dfrac{e^{2x}+2e^{0}+e^{-2x}}{4}-\dfrac{ e^{2x}-2e^{0}+e^{-2x}}{4}=\dfrac{2+2}{4}=1 \end{eqnarray*}
Numerous other identities involving hyperbolic functions can be established. We list some below.
| Sum formulas: | \begin{eqnarray*} \sinh ( A+B) &=&\sinh A\cosh B+\cosh A\sinh B \\ \cosh ( A+B) &=&\cosh A\cosh B+\sinh A\sinh B \end{eqnarray*} |
| Even/odd properties: | \begin{eqnarray*} \sinh ( -A) =-\sinh A\qquad \cosh ( -A) =\cosh A \end{eqnarray*} |
The derivations of these identities are left as exercises. (See Problems 17–20.)
NOW WORK
3 Differentiate Hyperbolic FunctionsPrinted Page 245
Since the hyperbolic functions are algebraic combinations of e^{x} and e^{-x}, they are differentiable at all real numbers for which they are defined. For example, \begin{eqnarray*} \dfrac{d}{dx}\sinh x &=&\dfrac{d}{dx}\left( \dfrac{e^{x}-e^{-x}}{2}\right) = \dfrac{1}{2}\left[ \dfrac{d}{dx}e^{x}-\dfrac{d}{dx}e^{-x}\right] =\dfrac{1}{2 }( e^{x}+e^{-x}) =\cosh x\\ \dfrac{d}{dx}\cosh x&=&\dfrac{d}{dx}\left( \dfrac{e^{x}+e^{-x}}{2}\right) = \dfrac{1}{2}\left[ \dfrac{d}{dx}e^{x}+\dfrac{d}{dx}e^{-x}\right] =\dfrac{1}{2 }( e^{x}-e^{-x}) =\sinh x\\ \dfrac{d}{dx}{\mathop{\rm{csch}}}~x&=&\dfrac{d}{dx}\left( \dfrac{1}{\sinh x}\right) = \dfrac{-\dfrac{d}{dx}\sinh x}{\sinh ^{2}x}=\dfrac{-\cosh x}{\sinh ^{2}x}=- \dfrac{1}{\sinh x}\cdot \dfrac{\cosh x}{\sinh x}\\ &=&-{\mathop{\rm{csch}}}~x\coth x \end{eqnarray*}
The formulas for the derivatives of the hyperbolic functions are listed below. \bbox[5px, border:1px solid black, #F9F7ED]{ {\dfrac{d}{dx}\sinh x=\cosh x\quad\dfrac{d}{dx}\tanh x=\sec\!{\rm h}^{2}\,x\quad\dfrac{d}{dx}\csc\!{\rm h}\,x=-\csc\!{\rm h}\,x\coth x\\ \dfrac{d}{dx}\cosh x =\sinh x\quad\dfrac{d}{dx}\coth x=-\csc\!{\rm h}^{2}\,x\quad\dfrac{d}{dx}\sec\!{\rm h}\,x=-\sec\!{\rm h}\,x\tanh x} }
EXAMPLE 3Differentiating Hyperbolic Functions
Find y^\prime .
- (a) y=x^{2}-2\sinh x
- (b) y=\cosh (x^{2}+1)
Solution
(a) y^\prime =\dfrac{d}{dx}( x^{2}-2\sinh x) =2x-2\dfrac{d}{dx}\sinh x=2x-2\cosh x
(b) We use the Chain Rule with y=\cosh u and u=x^{2}+1. y^\prime =\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot \dfrac{du}{dx}=\sinh u\cdot 2x=2x\sinh (x^{2}+1)
NOW WORK
246
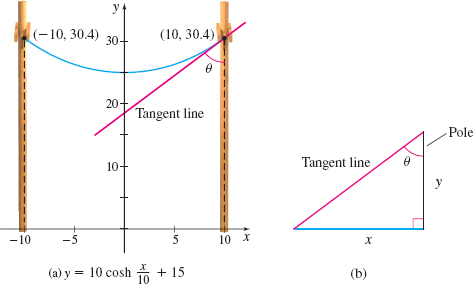
EXAMPLE 4Finding the Angle Between a Catenary and Its Support
A cable is suspended between two poles of the same height that are 20{\,{\rm{m}}} apart, as shown in Figure 29(a). If the poles are placed at (-10,0) and (10,0), the equation that models the height of the cable is y=10\cosh \dfrac{x}{10}+15. Find the angle \theta at which the cable meets a pole.
Solution
The slope of the tangent line to the catenary is given by y^\prime =\dfrac{d}{dx}\left( 10\cosh \dfrac{x}{10}+15\right) =10\cdot \dfrac{ 1}{10}\sinh \dfrac{x}{10}=\sinh \dfrac{x}{10}
At x=10, the slope m_{\tan } of the tangent line is m_{\tan }=\sinh \dfrac{10}{10}=\sinh 1.
The angle \theta at which the cable meets the pole equals the angle between the tangent line and the pole. To find \theta , we form a right triangle using the tangent line and the pole, as shown in Figure 29(b).
From Figure 29(b), we find that the slope of the tangent line is m_{\tan }=\dfrac{\Delta y}{\Delta x}=\sinh 1. Then \tan \theta =\dfrac{\Delta x}{\Delta y}=\dfrac{1}{\sinh 1}. So, \theta =\tan ^{-1}\left( \dfrac{1}{\sinh 1}\right) \approx 0.7050 radians \approx 40.4^{\circ}.
NOW WORK
4 Differentiate Inverse Hyperbolic FunctionsPrinted Page 246
The graph of y=\sinh x, shown in Figure 22, suggests that every horizontal line intersects the graph at exactly one point. In fact, the function y= \sinh x is one-to-one, and so it has an inverse function. We denote the inverse by y=\sinh ^{-1}x and define it as \bbox[5px, border:1px solid black, #F9F7ED]{ {y=\sinh ^{-1}x\quad\hbox{ if and only if }\quad x=\sinh y}}
NEED TO REVIEW?
A discussion on one-to-one functions and inverse functions can be found in Section P.4, pp. 32-37.
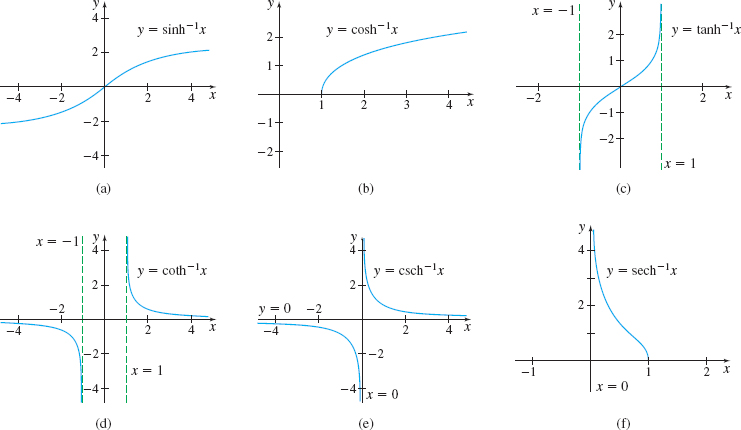
The domain of y=\sinh ^{-1}x is the set of real numbers, and the range is also the set of real numbers. See Figure 30(a).
The graph of y=\cosh x (see Figure 23) shows that every horizontal line above y=1 intersects the graph of y=\cosh x at two points so y=\cosh x is not one-to-one. However, if the domain of y=\cosh x is restricted to the nonnegative values of x, we have a one-to-one function that has an inverse. We denote the inverse function by y= \cosh ^{-1}x and define it as \bbox[5px, border:1px solid black, #F9F7ED]{ {y=\cosh ^{-1}x\quad\hbox{ if and only if }\quad x=\cosh y \quad y ≥ 0}}
247
The domain of y=\cosh ^{-1}x is x ≥ 1, and the range is y ≥ 0. See Figure 30(b).
The other inverse hyperbolic functions are defined similarly. Their graphs are given in Figure 30(c)–(f).
Since the hyperbolic functions are defined in terms of the exponential function, the inverse hyperbolic functions can be expressed in terms of natural logarithms.
\bbox[5px, border:1px solid black, #F9F7ED]{ {y=\sinh ^{-1}x=\ln \big(x+\ \sqrt{x^{2}+1}\big)\qquad \hbox{for all real }x}} \bbox[5px, border:1px solid black, #F9F7ED]{ {y=\cosh ^{-1}x=\ln \big( x+\ \sqrt{x^{2}-1}\big)\qquad x ≥ 1}} \bbox[5px, border:1px solid black, #F9F7ED]{ {y=\tanh ^{-1}x=\dfrac{1}{2}\ln \left( \dfrac{1+x}{1-x}\right)\qquad \vert x\vert <1}} \bbox[5px, border:1px solid black, #F9F7ED]{ {y=\coth ^{-1}x=\dfrac{1}{2}\ln \left( \dfrac{x+1}{x-1}\right)\qquad \vert x\vert >1}}
We show that \sinh ^{-1}x=\ln \big( x+\ \sqrt{x^{2}+1}\big) here, and leave the others as exercises. (See Problems 61–63.)
EXAMPLE 5Expressing the Inverse Hyperbolic Sine Function as a Natural Logarithm
Express y=\sinh ^{-1}x as a natural logarithm.
Solution Since y=\sinh ^{-1}x, where x=\sinh y, we have \begin{eqnarray*} x &=&\dfrac{e^{y}-e^{-y}}{2} \\ 2xe^{y} &=&( e^{y}) ^{2}-1\qquad {\color{#0066A7}{\hbox{Multiply both sides by }2e^{y}.}} \\ ( e^{y}) ^{2}-2xe^{y}-1 &=&0 \end{eqnarray*}
248
This is a quadratic equation in e^{y}. Use the quadratic formula and solve for e^{y}. \begin{eqnarray*} e^{y} &=&\dfrac{2x\pm \ \sqrt{4x^{2}+4}}{2}\qquad \\ e^{y} &=&x\pm \ \sqrt{x^{2}+1}\qquad\ {\color{#0066A7}{\hbox{ Simplify.}}} \end{eqnarray*}
Since e^{y}>0 and x<\ \sqrt{x^{2}+1} for all x, the minus sign on the right side is not possible. As a result, e^{y}=x+\ \sqrt{x^{2}+1} so that y=\sinh ^{-1}x=\ln ( x+\ \sqrt{x^{2}+1})
NEED TO REVIEW?
The quadratic equation is discussed in Appendix A.1 (p. A-3).
NOW WORK
EXAMPLE 6Differentiating an Inverse Hyperbolic Sine Function
Show that if y=\sinh ^{-1}x, then \bbox[5px, border:1px solid black, #F9F7ED]{ {y^\prime =\dfrac{d}{dx}\sinh ^{-1}x=\dfrac{1}{\ \sqrt{x^{2}+1}}.}}
Solution Since y=\sinh ^{-1}x=\ln \big( x+\ \sqrt{x^{2}+1}\big), we have \begin{eqnarray*} y^\prime &=&\dfrac{d}{dx}\sinh ^{-1}x=\dfrac{d}{dx}\left[ \ln \big( x+\ \sqrt{x^{2}+1}\big) \right] \underset{\underset{\color{#0066A7}{\hbox{\(\tfrac{d}{dx}\ln (u)=\tfrac{u^{\,\prime} ( x) }{u( x) }\)}}}{\color{#0066A7}{\uparrow }}}{=} \dfrac{\dfrac{d}{dx}\big( x+\ \sqrt{x^{2}+1}\big) }{x+\ \sqrt{x^{2}+1}}\\ &=&\dfrac{1+\dfrac{1}{2}(x^{2}+1) ^{-1/2}\cdot 2x}{x+\ \sqrt{x^{2}+1}}=\dfrac{1+\dfrac{x}{\ \sqrt{x^{2}+1}}}{x+\ \sqrt{x^{2}+1}}=\dfrac{\dfrac{\ \sqrt{ x^{2}+1}+x}{\ \sqrt{x^{2}+1}}}{x+\ \sqrt{x^{2}+1}}\\ &=&\dfrac{x+\ \sqrt{x^{2}+1}}{ ( x+\ \sqrt{x^{2}+1}) \ \sqrt{x^{2}+1}}=\dfrac{1}{\ \sqrt{x^{2}+1}} \end{eqnarray*}
NOW WORK
Similarly, we have the following derivative formulas. If y=\cosh ^{-1}x, then \bbox[5px, border:1px solid black, #F9F7ED]{ {y^\prime =\dfrac{d}{dx}\cosh ^{-1}x=\dfrac{1}{\ \sqrt{x^{2}-1}}\qquad x>1}}
If y=\tanh ^{-1}x, then \bbox[5px, border:1px solid black, #F9F7ED]{ {y^\prime =\dfrac{d}{dx}\tanh ^{-1}x=\dfrac{1}{1-x^{2}}\qquad \vert x\vert <1}}
EXAMPLE 7Differentiating an Inverse Hyperbolic Tangent Function
Find y^\prime if y=\tanh ^{-1}\ \sqrt{x}.
Solution We use the Chain Rule with y=\tanh ^{-1}u and u=\ \sqrt{x}. Then \begin{eqnarray*} y^\prime &=&\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot \dfrac{du}{dx}=\dfrac{d}{du} \tanh ^{-1}u\cdot \dfrac{d}{dx}\ \sqrt{x}\\ &=&\dfrac{1}{{1-u^{2}}}\cdot \dfrac{1}{2\ \sqrt{x}}=\dfrac{1}{ {1-x}}\cdot \dfrac{1}{2\ \sqrt{x}}=\dfrac{\ \sqrt{x}}{2x(1-x)}\qquad \ {\color{#0066A7}{\hbox{\(u=\ \sqrt{x}\)}}} \nonumber \\ \end{eqnarray*}