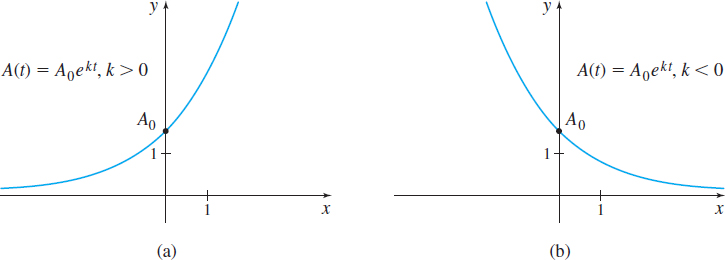5.5 The Indefinite Integral; Growth and Decay ModelsPrinted Page 379
379
OBJECTIVES
When you finish this section, you should be able to:
The Fundamental Theorem of Calculus establishes an important relationship between definite integrals and antiderivatives: the definite integral ∫baf(x)dx can be found easily if an antiderivative of f can be found. Because of this, it is customary to use the integral symbol ∫ as an instruction to find all antiderivatives of a function.
DEFINITION Indefinite Integral
The expression ∫f(x)dx, called the indefinite integral of {\boldsymbol f}, is defined as, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt]{ \int f(x)\, dx=F(x) +C }}
where F is any function for which \dfrac{d}{dx} F(x) =f(x) and C is a number, called the constant of integration.
CAUTION
In writing an indefinite integral \int f(x) \,dx, remember to include the “{ dx}.”
For example, \int ({x^{2}+1})\, dx=\dfrac{x^{3}}{3}+x +C \qquad {\color{#0066A7}{ \dfrac{d}{dx}\left( \dfrac{x^{3}}{3}+x+C\right) = \dfrac{3x^{2}}{3}+1+0=x^{2}+1}}
The process of finding either the indefinite integral \int f(x)dx or the definite integral \int_{a}^{b}f(x)dx is called integration, and in both cases the function f is called the integrand.
NOTE
The definite integral \int_{a}^{b}f(x)\, dx is a number; the indefinite integral \int f(x)\, dx is a family of functions.
It is important to distinguish between the definite integral {\int_{a}^{b}{f(x)\,dx}} and the indefinite integral \int f(x)\,dx. The definite integral is a number that depends on the limits of integration a and b. In contrast, the indefinite integral of f is a family of functions F(x) +C, C a constant, for which F^\prime (x) =f(x) . For example, \int_{0}^{2}x^{2}dx=\left[ \dfrac{x^{3}}{3}\right] _{0}^{2}=\dfrac{8}{3}\qquad \int x^{2}dx=\dfrac{x^{3}}{3}+C
NEED TO REVIEW?
Refer to Table 7 in Appendix A.4, pp. A-32 to A-35.
We summarize the antiderivatives of some important functions in Table 1 below. Each entry is a result of a differentiation formula.
| Table of Integrals | |
|---|---|
| \int \, dx=x+C | \int \sec x\tan x\,dx=\sec x+C |
| \int x^{a }\, dx=\dfrac{x^{a +1}}{a +1}+C; a \neq -1 | \int \csc x\cot x\,dx=-\csc x+C |
| \int x^{-1}\, dx=\int \dfrac{1}{x}\, dx=\ln \vert x\vert +C | \int \csc ^{2}x\,dx=-\cot x+C |
| \int e^{x}\, dx=e^{x}+C | \int \dfrac{1}{\sqrt{1-x^{2}}} dx= \sin^{-1}x+C, \vert x\vert \lt1 |
| \int a^{x}\, dx=\dfrac{a^{x}}{\ln a}+C; a>0, a\neq 1 | \int \dfrac{1}{1+x^{2}}\, dx=\tan ^{-1}x+C |
| \int \sin x\,dx=-\cos x+C | \int \dfrac{1}{x\sqrt{x^{2}-1}}\, dx=\sec ^{-1}x+C\,, \vert x\vert >1 |
| \int \cos x\,dx=\sin x+C | \int \sinh x\,dx=\cosh x+C\, |
| \int \sec ^{2}x\,dx=\tan x+C | \int \cosh x\,dx=\sinh x+C |
1 Find Indefinite IntegralsPrinted Page 379
EXAMPLE 1Finding Indefinite Integrals
Find:
- (a) \int x^{4}\, dx
- (b) \int \sqrt{x} dx
- (c) \int \dfrac{\sin x}{\cos ^{2}x} dx
Solution (a) All the antiderivatives of f(x)=x^{4} are F(x) =\dfrac{x^{5}}{5}+C, so \int x^{4}\, dx=\dfrac{x^{5}}{5}+C
380
(b) All the antiderivatives of f(x) =\sqrt{x} =x^{1/2} are F(x) =\dfrac{x^{3/2}}{\dfrac{3}{2}}+C=\dfrac{2x^{3/2}}{3}+C, so \int \sqrt{x} dx=\dfrac{2x^{3/2}}{3}+C
NEED TO REVIEW?
Trigonometric identities are discussed in Appendix A.4, pp. A-32 to A-35.
(c) No antiderivative in Table 1 corresponds to f(x)=\dfrac{\sin x}{\cos ^{2}x}, so we begin by using trigonometric identities to rewrite \dfrac{\sin x}{\cos ^{2}x} in a form whose antiderivative is recognizable. \dfrac{\sin x}{\cos ^{2}x}=\dfrac{\sin x}{\cos x\cdot \cos x}=\dfrac{1}{\cos x}\cdot \dfrac{\sin x}{\cos x}=\sec x\tan x
Then \int \dfrac{\sin x}{\cos ^{2}x}\, dx=\int \sec x\tan x dx=\sec x+C
NOW WORK
2 Use Properties of Indefinite IntegralsPrinted Page 380
Since the definite integral and the indefinite integral are closely related, properties of indefinite integrals are very similar to those of definite integrals:
- Derivative of an Integral: \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{d}{dx}\left[ \int f(x)\,dx\right] =f(x) }}\tag{1}
381
Property (1) is a consequence of the definition of \int f(x)\,dx. For example, \dfrac{d}{dx} \int \sqrt{x^{2}+1}\,dx=\sqrt{x^{2}+1} \qquad \dfrac{d}{dt}\int e^{t}\cos t\,dt=e^{t}\cos t
- Integral of the Sum of Two Functions: \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int\, [f(x)+g(x)]\,dx=\int f(x)\,dx+\int g(x)\,dx }}\tag{2}
IN WORDS
The indefinite integral of a sum of two functions equals the sum of the indefinite integrals.
The proof of property (2) follows directly from properties of derivatives, and is left as an exercise. See Problem 68.
- Integral of a Constant Times a Function: If k is a constant, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int k\,f(x)\,dx=k\int f(x)\,dx }}\tag{3}
IN WORDS
To find the indefinite integral of a constant k times a function f, find the indefinite integral of f and then multiply by k.
To prove property (3), differentiate the right side of the (3). \begin{eqnarray*} {\dfrac{{d}}{{dx}}}{\left[ {k\int {f(x)\,dx}}\right] } \underset{\underset{{\color{#0066A7}{\hbox{Constant Multiple Rule}}}}{\color{#0066A7}{\uparrow}}} {=} k{\left[ {{\dfrac{{d}}{{dx}}} \int {f(x)\,dx}}\right] } \underset{\underset{{\color{#0066A7}{\hbox{Property (1)}}}}{\color{#0066A7}{\uparrow}}} {=}k\,f(x) \end{eqnarray*}
EXAMPLE 2Using Properties of the Indefinite Integral
\begin{eqnarray*} \int (2x^{1/3}+5x^{-1})\,dx &=& \int 2x^{1/3}\,dx+\int \dfrac{5}{x}\,dx=2\int x^{1/3}\,dx+5\int \dfrac{1}{x}\,dx \\ &=& 2\cdot {\dfrac{{x^{4/3}}}{{{\dfrac{{4}}{{3} }}}}}+{5\ln \,}\vert x\vert +C={\dfrac{{3x^{4/3}}}{{2}}}+5\ln \,\vert x\vert +C \end{eqnarray*}
NOW WORK
Sometimes an appropriate algebraic manipulation is required before integrating.
EXAMPLE 3Using Properties of the Indefinite Integral
- (a) \begin{eqnarray*} \int \left( \dfrac{12}{x^{5}}+\dfrac{1}{\sqrt{x}}\right) dx&=&12\int \dfrac{1}{x^{5}}\,dx+\int \dfrac{1}{\sqrt{x}}\,dx=12\int x^{-5}\,dx+\int x^{-1/2}\,dx \\ &=& 12\left( \dfrac{x^{-4}}{{-}4}\right) +\dfrac{ x^{1/2}}{\dfrac{1}{2}}+C = -\dfrac{3}{x^{4}}+2\sqrt{x}+C \end{eqnarray*}
- (b) \begin{eqnarray*} \int \dfrac{x^{2}+6}{x^{2}+1} dx & \underset{\underset{{\color{#0066A7}{\hbox{Algebra}}}}{\color{#0066A7}{\uparrow}}}{=}& \int \dfrac{( x^{2}+1) +5}{x^{2}+1} dx =\int \left[ \dfrac{x^{2}+1}{x^{2}+1}+\dfrac{5}{x^{2}+1}\right] dx \\ &=&\int \left[ 1+\dfrac{5}{x^{2}+1}\right] dx \underset{\underset{{\color{#0066A7}{\hbox{Sum Property}}}}{\color{#0066A7}{\uparrow }}} {=} \int dx+\int \dfrac{5}{x^{2}+1} dx \\ &=&\int dx+5\int \dfrac{1}{x^{2}+1} dx=x+5 \tan ^{-1}x+C \end{eqnarray*}
NOW WORK
3 Solve Differential Equations Involving Growth and DecayPrinted Page 382
382
There are situations in science and nature, such as radioactive decay, population growth, and interest paid on an investment, in which a quantity A varies with time t in such a way that the rate of change of A with respect to t is proportional to A itself. These situations can be modeled by the differential equation \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{{\it dA}}{dt}=kA }}\tag{4}
where k\neq 0 is a real number:
- If k \gt 0, then \dfrac{{\it dA}}{dt}=kA, the rate of change of A with respect to t is positive, and the amount A is increasing.
- If k\lt0, then \dfrac{{\it dA}}{dt}=kA, the rate of change of A with respect to t is negative, and the amount A is decreasing.
Suppose that the initial amount A_{0} of the substance is known, giving us the boundary condition, or initial condition, A=A(0) =A_{0} when t=0.
We solve differential equations of the form \dfrac{\it dA}{dt}={\it kA} by writing \dfrac{{\it dA}}{dt}={\it kA} as \dfrac{{\it dA}}{A}=k\,dt.* Then we integrate both sides of the equation, on the left with respect to A and on the right with respect to t. \begin{eqnarray*} \int \dfrac{1}{A} {\it dA} &=&\int k\,dt \\ \ln \left\vert A\right\vert &=&kt+C \\ \ln A &=&k\,t+C\qquad A \gt 0 \end{eqnarray*}
*This technique for solving a differential equation, called separating the variables, is discussed in more detail in Chapter 16.
The initial condition requires that A=A_{0} when t=0. Then \ln A_{0}=C, so \begin{eqnarray*} \ln A &=&kt+\ln A_{0} \\ \ln A-\ln A_{0} &=&kt \\ \ln \dfrac{A}{A_{0}} &=&kt \\ \dfrac{A}{A_{0}} &=&e^{kt} \\ A &=&A_{0}e^{kt}\\ \end{eqnarray*}
The solution to the differential equation \dfrac{{\it dA}}{dt}=kA is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ A=A_{0}e^{kt}}}\tag{5}
where A_{0} is the initial amount.
Functions A=A(t) whose rates of change are \dfrac{{\it dA}}{dt}=kA are said to follow the exponential law, or the law of uninhibited growth or decay—or in a business context, the law of continuously compounded interest. Figure 31, shows the graphs of the function A(t) =A_{0}e^{kt} for both k>0 and k\lt0.
383
EXAMPLE 4Solving a Differential Equation for Growth
NOTE
Example 4 is a model of uninhibited growth; it accurately reflects growth in early stages. After a time, growth no longer continues at a rate proportional to the number present. Factors, such as disease, lack of space, and dwindling food supply, begin to affect the rate of growth.
Assume that a colony of bacteria grows at a rate proportional to the number of bacteria present. If the number of bacteria doubles in 5 hours (h), how long will it take for the number of bacteria to triple?
Solution Let N(t) be the number of bacteria present at time t. Then the assumption that this colony of bacteria grows at a rate proportional to the number present can be modeled by \dfrac{dN}{dt}=kN
where k is a positive constant of proportionality. To find k, we write the differential equation as \dfrac{dN}{N}=kdt and integrate both sides. This differential equation is of form (4), and its solution is given by (5). So, we have N(t) =N_{0}e^{kt}
where N_{0} is the initial number of bacteria in the colony. Since the number of bacteria doubles to 2N_{0} in 5h, \begin{eqnarray*} N(5) =N_{0}\,e^{5k} &=& 2N_{0} \\ e^{5k} &=&2 \\ k &=&\dfrac{1}{5}\ln 2 \end{eqnarray*}
The time t required for this colony to triple obeys the equation \begin{eqnarray*} N(t) &=&3N_{0} \\ N_{0}e^{kt} &=&3N_{0} \\ e^{kt} &=&3 \\ t &=&\dfrac{1}{k}\ln 3 \underset{\underset{{\color{#0066A7}{\hbox{\( k=\tfrac{1}{5}\ln 2\)}}}}{\color{#0066A7}{\uparrow }}}{=}5\dfrac{\ln 3}{\ln 2}\approx 8 \end{eqnarray*}
The number of bacteria will triple in about 8h.
NOW WORK
For a radioactive substance, the rate of decay is proportional to the amount of substance present at a given time t. That is, if A=A(t) represents the amount of a radioactive substance at time t, then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{{\it dA}}{dt}=kA }}
384
ORIGINS
Willard F. Libby (1908-1980) grew up in California and went to college and graduate school at UC Berkeley. Libby was a physical chemist who taught at the University of Chicago and later at UCLA. While at Chicago, he developed the methods for using natural carbon-14 to date archaeological artifacts. Libby won the Nobel Prize in Chemistry in 1960 for this work.
where k\lt0 and depends on the radioactive substance. The half-life of a radioactive substance is the time required for half of the substance to decay.
Carbon dating, a method for determining the age of an artifact, uses the fact that all living organisms contain two kinds of carbon: carbon-12 (a stable carbon) and a small proportion of carbon-14 (a radioactive isotope). When an organism dies, the amount of carbon-12 present remains unchanged, while the amount of carbon-14 begins to decrease. This change in the amount of carbon-14 present relative to the amount of carbon-12 present makes it possible to calculate how long ago the organism died.
EXAMPLE 5Solving a Differential Equation for Decay
The skull of an animal found in an archaeological dig contains about 20% of the original amount of carbon-14. If the half-life of carbon-14 is 5730 years, how long ago did the animal die?

Solution Let A=A(t) be the amount of carbon-14 present in the skull at time t. Then A satisfies the differential equation \dfrac{{\it dA}}{dt}=kA, whose solution is A=A_{0}e^{kt}
where A_{0} is the amount of carbon-14 present at time t=0. To determine the constant k, we use the fact that when t=5730, half of the original amount A_{0} remains. \begin{eqnarray*} \dfrac{1}{2}A_{0} &=&A_{0}e^{5730k} \\ \dfrac{1}{2} &=&e^{5730k} \\ 5730k &=&\ln \dfrac{1}{2} = -\ln 2 \\ k &=&-\dfrac{\ln 2}{5730} \end{eqnarray*}
The relationship between the amount A of carbon-14 present and the time t is A(t) =A_{0}e^{\left( -\ln 2/5730\right) t}
In this skull, 20% of the original amount of carbon-14 remains, so A(t) =0.20A_{0}. \begin{eqnarray*} 0.20A_{0} &=&A_{0}e^{( -\ln 2/5730) t} \\ 0.20 &=&e^{( -\ln 2/5730) t} \end{eqnarray*}
Now, we take the natural logarithm of both sides. \begin{eqnarray*} \ln 0.20 &=&-\dfrac{\ln 2}{5730}\cdot t \\ t &=&-5730\cdot \dfrac{\ln 0.20}{\ln 2}\approx 13{,}300 \end{eqnarray*}
The animal died approximately 13,300 years ago.