9.5 Assess Your UnderstandingPrinted Page 676
Concepts and Vocabulary
True or False A cardioid passes through the pole.
True
Multiple Choice The equations for cardioids and limaçons are very similar. They all have the form r=a±b cosθorr=a±b sinθ,a>0,b>0 The equations represent a limaçon with an inner loop if [(a) a<b, (b) a>b, (c) a=b]; a cardioid if [(a) a<b, (b) a>b, (c) a=b]; and a limaçon without an inner loop if [(a) a<b, (b) a>b, (c) a=b].
a, c, b
True or False The graph of r=sin(4θ) is a rose.
True
The rose r= cos(3θ) has __________ petals.
3
Skill Building
In Problems 5–12, for each polar equation:
(a) Graph the equation.
(b) Find parametric equations that represent the equation.
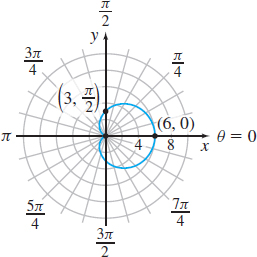
r=2+2 cosθ
- (a)
- (b) x=2(1+cosθ) cosθ,
y=2(1+cosθ) sinθ
r=3−3sinθ
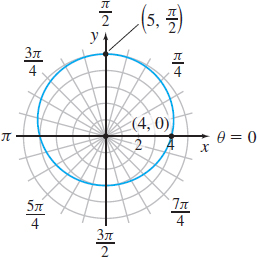
r=4−2 cosθ
- (a)

- (b) x=2(2−cosθ) cosθ, y=2(2−cosθ) sinθ
r=2+sinθ
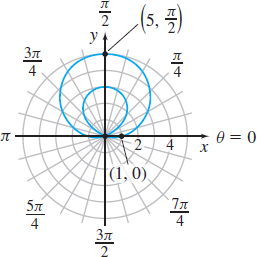
r=1+2sinθ
- (a)
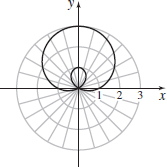
- (b) x=(1+2 sinθ) cosθ, y=(1+2 sinθ) sinθ
r=2−3 cosθ
r=sin(3θ)
- (a)
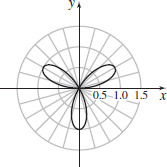
- (b) x=sin(3θ) cosθ,
y=sin(3θ) sinθ
r=4 cos(4θ)
In Problems 13–18, graph each pair of polar equations on the same polar grid. Find polar coordinates of the point(s) of intersection and label the point(s) on the graph.
r=8cosθ,r=2secθ
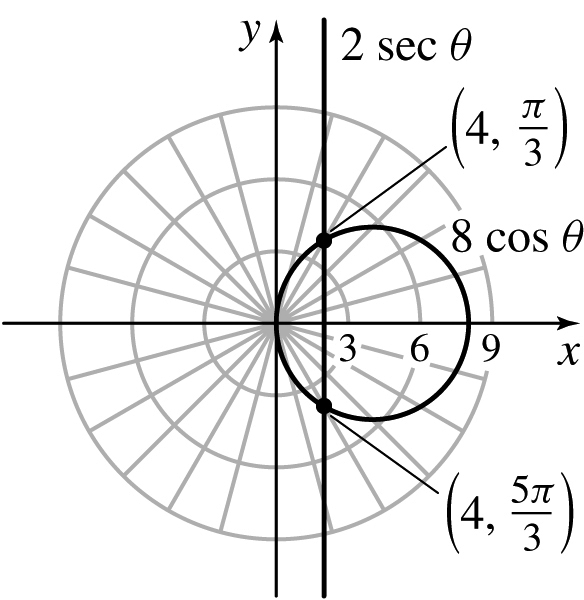
(4,π3),(4,5π3)
r=8sinθ,r=4cscθ
r=sinθ,r=1+ cosθ

(1,π2),(0,π)
r=3,r=2+2 cosθ
r=1+sinθ,r=1+ cosθ
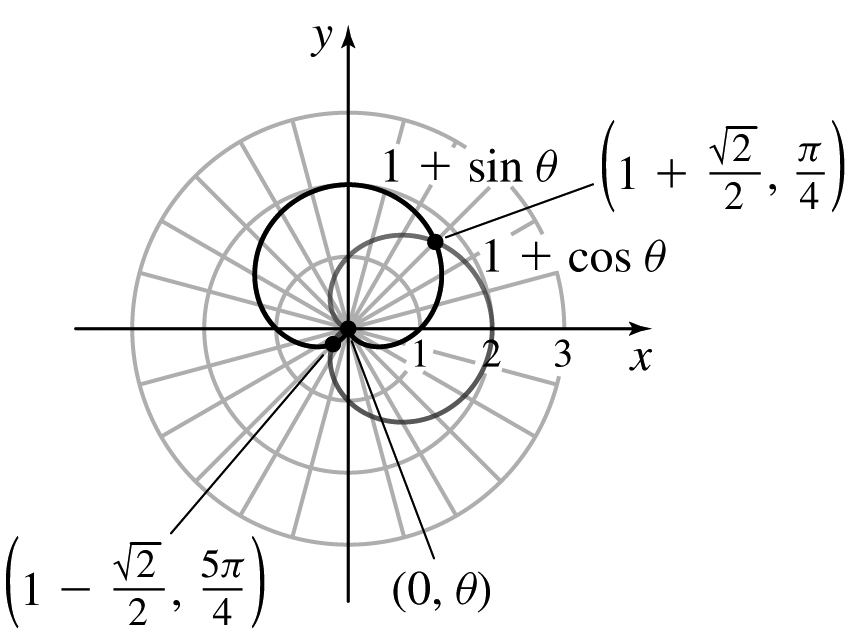
(1+√22,π4)
(1−√22,5π4)
(0,θ), (the pole)
r=1+ cosθ,r=3 cosθ
In Problems 19–22, find the arc length of each curve.
r=f(θ)=eθ/2fromθ=0toθ=2
√5(e−1)
r=f(θ)=e2θfromθ=0toθ=2
r=f(θ)= cos2θ2fromθ=0toθ=π
2
r=f(θ)=sin2θ2fromθ=0toθ=π
Applications and Extensions
In Problems 23–26, the polar equation for each graph is either r=a+b cosθ or r=a+b sinθ,a>0,b>0. Select the correct equation and find the values of a and b.
3+3 cosθ
4+sinθ
In Problems 27–32, find an equation of the tangent line to each curve at the given number. (Hint: Find parametric equations that represent each polar equation. See Section 9.2.)
r=2 cos(3θ)atθ=π6
y=√33x
r=3sin(3θ)atθ=π3
r=2+ cosθatθ=π4
y=(√2−2)x+5√22−12
r=3−sinθatθ=π6
677
r=4+5sinθatθ=π4
y=−(1+5√24) x+57√28+10
r=1−2 cosθatθ=π4
Lemniscates Graphs of polar equations of the form r2=a2 cos(2θ) or r2=a2sin(2θ), where a≠0, are called lemniscates. A lemniscate passes through the pole twice and is shaped like the infinity symbol ∞.
In Problems 33–36, for each equation:
(a) Graph the lemniscate.
(b) Find parametric equations that represent the equation.
r2=4 sin(2θ)
- (a)
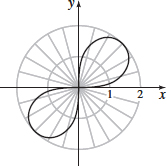
- (b) x=2√sin(2θ)cosθ,
y=2√sin(2θ)sinθ
r2=9 cos(2θ)
r2= cos(2θ)
- (a)
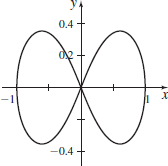
- (b) x=√cos(2θ)cosθ,
y=√cos(2θ)sinθ
r2=16 sin(2θ)
In Problems 37–48:
(a) Graph each polar equation.
(b) Find parametric equations that represent each equation.
r=21− cosθ (parabola)
- (a)
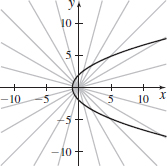
- (b) x=2 cosθ1−cosθ,
y=2 sinθ1−cosθ
r=11− cosθ (parabola)
r=13−2 cosθ (ellipse)
- (a)
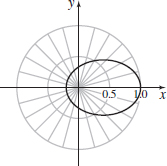
- (b) x=cosθ3−2 cosθ,
y=sinθ3−2 cosθ
r=21−2 cosθ (hyperbola)
r=θ; θ≥0 (spiral of Archimedes)
- (a)
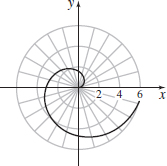
- (b) x=θ cosθ,
y=θ sinθ
r=3θ; θ>0 (reciprocal spiral)
r=cscθ−2;0<θ<π (conchoid)
- (a)
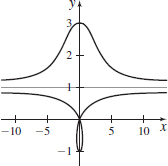
- (b) x=(cscθ−2) cosθ,
y=(cscθ−2) sinθ
r=3−12cscθ (conchoid)
r=sinθtanθ (cissoid)
- (a)
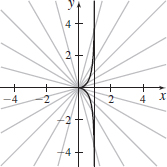
- (b) x=sin2θ,
y=sin2θ tanθ
r= cosθ2
r=tanθ (kappa curve)
- (a)

- (b) x=sinθ,
y=sinθ tanθ
r=cotθ (kappa curve)
Show that r=4(cosθ+1) and r=4(cosθ−1) have the same graph.
See Student Solutions Manual.
Show that r=5(sinθ+1) and r=5(sinθ−1) have the same graph.
Arc Length Find the arc length of the spiral r=θ from θ=0 to θ=2π.
π√1+4π2+12ln(2π+√4π2+1)
Arc Length Find the arc length of the spiral r=3θ from θ=0 to θ=2π.
Perimeter Find the perimeter of the cardioid r=f(θ)=1− cosθ, −π≤θ≤π.
8
 Exploring Using Graphing Technology
Exploring Using Graphing Technology- (a) Graph r1=2 cos(4θ). Clear the screen and graph r2=2 cos(6θ). How many petals does each of the graphs have?
- (b) Clear the screen and graph, in order, each on a clear screen, r1=2 cos(3θ),r2=2 cos(5θ), and r3=2 cos(7θ). What do you notice about the number of petals? Do the results support the definition of a rose?
 Exploring Using Graphing Technology Graph r1=3−2 cosθ. Clear the screen and graph r2=3+2 cosθ. Clear the screen and graph r3=3+2sinθ. Clear the screen and graph r4=3−2sinθ. Describe the pattern.
Exploring Using Graphing Technology Graph r1=3−2 cosθ. Clear the screen and graph r2=3+2 cosθ. Clear the screen and graph r3=3+2sinθ. Clear the screen and graph r4=3−2sinθ. Describe the pattern.
Answers will vary.
Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the cardioid r=1−sinθ discussed in Example 1.
Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the cardioid r=3+3 cosθ.
Horizontal: y=9√34, y=−9√34 vertical: x=−34, x=6
 Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the limaçon with an inner loop r=1+2 cosθ discussed in Example 3.
Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the limaçon with an inner loop r=1+2 cosθ discussed in Example 3.
 Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the rose with four petals r=2 cos(2θ),0≤θ≤2π, discussed in Example 4.
Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the rose with four petals r=2 cos(2θ),0≤θ≤2π, discussed in Example 4.
Horizontal: y=43√6, y=−43√6, y=2, y=−2; vertical: x=43√6, x=−43√6, x=2, x=−2
 Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the spiral r=eθ/5 discussed in Example 5.
Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the spiral r=eθ/5 discussed in Example 5.
 Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the lemniscate r2=4sin(2θ).
Horizontal and Vertical Tangent Lines Find the horizontal and vertical tangent lines of the lemniscate r2=4sin(2θ).
Horizontal: y=33/4√2, y=−33/4√2; vertical: x=33/4√2, x=−33/4√2
Test for Symmetry Symmetry with respect to the polar axis can be tested by replacing θ with −θ. If an equivalent equation results, the graph is symmetric with respect to the polar axis.
- (a) Explain why this test is valid.
- (b) Use the test to show that r=3+2 cosθ is symmetric with respect to the polar axis.
Test for Symmetry Symmetry with respect to the pole can be tested by replacing r by −r or by replacing θ by θ+π. If either substitution produces an equivalent equation, the graph is symmetric with respect to the pole.
- (a) Explain why these tests are valid.
- (b) Show that r2=4 sin(2θ) is symmetric with respect to the pole.
- (a) Answers will vary.
- (b) See Student Solutions Manual.
Test for Symmetry Symmetry with respect to the line θ=π2 can be tested by replacing θ by π−θ. If an equivalent equation results, the graph is symmetric with respect to the line θ=π2.
- (a) Explain why this test is valid.
- (b) Use the test to show that r=2 cos(2θ) is symmetric with respect to the line θ=π2.
Challenge Problems
Tests for Symmetry The three tests for symmetry described in Problems 62–64 are sufficient conditions for symmetry, but they are not necessary conditions. That is, an equation may fail these tests and still have a graph that is symmetric with respect to the polar axis, the line θ=π2, or the pole.
Testing for Symmetry The graph of r=sin(2θ) (a rose with four petals) is symmetric with respect to the polar axis, the line θ=π2, and the pole. Show that the test for symmetry with respect to the pole (see Problem 63) works, but the test for symmetry with respect to the polar axis fails (see Problem 62).
See Student Solutions Manual.
678
Arc Length Find the entire arc length of the curve r=a sin3θ3, a>0. (Hint: Use parametric equations.)
 Arc Length of a Rose Petal
Arc Length of a Rose Petal- (a) Graph the rose r=4sin(5θ).
- (b) The petal in the first quadrant begins when θ=0 and ends when θ=α. Find α.
- (c) Find the length s of the petal described in (b).
- (a)
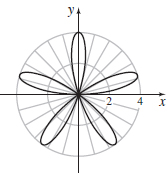
- (b) α=π5
- (c) ≈8.404